Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
ГЛАВА 3. МОДЕЛЬНОЕ ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЦИФРОВЫХ СИСТЕМ УПРАВЛЕНИЯ3.1. Исследование устойчивости с помощью корней характеристического уравненияВ работе для исследования устойчивости динамических объектов с различными алгебраическими критериями использовались так называемые тестовые объекты, являющиеся моделями реальных объектов с различными конфигурациями нулей и полюсов дискретной передаточной функции Пример 1. Определить устойчивость дискретной системы с передаточной функцией 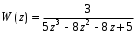 . .Характеристическое уравнение имеет вид 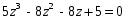 . .Разложим уравнение на множители и получим: 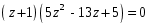 Определим корни характеристического уравнения 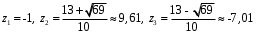 . .Система находится на границе устойчивости, так как один из корней ее характеристического уравнения по модулю равен единице. Пример 2. Определить устойчивость дискретной системы с передаточной функцией 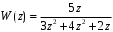 . .Решение: Характеристическое уравнение имеет вид: 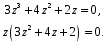 Определим корни характеристического уравнения: 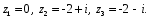 Определим модуль корней: 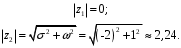 Система неустойчива, так как два последних корня ее характеристического уравнения по модулю больше единицы, что опровергает условие устойчивости. Пример 3. Определить устойчивость дискретной системы с передаточной функцией 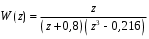 . .Решение: Характеристическое уравнение имеет вид: 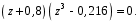 Определим корни характеристического уравнения: 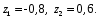 Система устойчива, так как корни ее характеристического уравнения по модулю меньше единицы, что соответствует условию устойчивости. 3.2. Исследование устойчивости с помощью билинейного преобразованияПример 4. С помощью билинейного преобразования исследовать на устойчивость дискретную функцию вида: 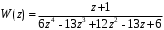 Решение: 1) В характеристическое уравнение подставим 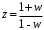 : :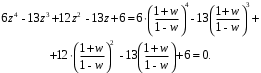 2) Поученное уравнение умножим на 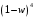 : :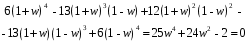 3) Определяем устойчивость по критерию Гурвица: 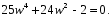 Все определители Гурвица будут равны нулю, так как коэффициенты с нечетными индексами a1 и a3 равны нулю. Следовательно, система является неустойчивой. Пример 5. С помощью билинейного преобразования исследовать на устойчивость дискретную функцию вида: 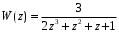 Решение: 1) В характеристическое уравнение подставим 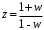 : :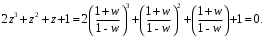 2) Поученное уравнение умножим на 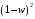 : :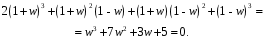 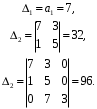 Все определители оказались положительными, что соответствует условию устойчивости. Следовательно, система устойчива. 3.3. Применение критерия устойчивости ДжуриПример 6. С помощью критерия Джури определить устойчивость дискретной системы, если передаточная функция в форме z – преобразования имеет вид: 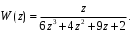 Решение: Характеристическое уравнение функции имеет вид: 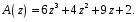 Проверяем необходимые условия критерия: 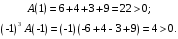 Поскольку эти легко вычисляемые неравенства удовлетворяются, то имеет смысл вычислять коэффициент 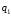 . .Составим обратный полином путём перестановки коэффициентов в обратном примере. 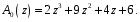 Разделим A(z) на A0(z):  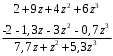 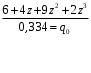 ; ;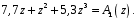 Умножив его на 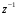 получаем: получаем: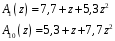 Делим 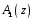 на на 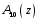 : : 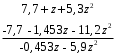 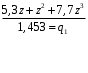 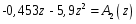 Результаты расчёта показывают, что 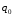 по модулю меньше единицы, а по модулю меньше единицы, а 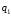 по модулю больше единицы, что опровергает последнее условие устойчивости. Следовательно, цифровая система неустойчива. по модулю больше единицы, что опровергает последнее условие устойчивости. Следовательно, цифровая система неустойчива.Пример 7. С помощью критерия Джури определить устойчивость дискретной системы, если передаточная функция в форме z – преобразования имеет вид: 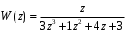 Решение: Характеристическое уравнение функции имеет вид: 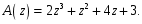 Здесь выполняется необходимое условие устойчивости, т.к. все коэффициенты положительны. Следовательно, мы можем проверить условия данного критерия: 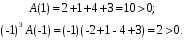 Поскольку эти легко вычисляемые неравенства удовлетворяются, то имеет смысл вычислять коэффициент 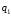 . .Составим обратный полином путём перестановки коэффициентов в обратном примере. 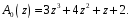 Разделим A(z) на A0(z):  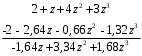 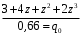 ; ;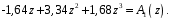 Умножив его на 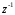 получаем: получаем: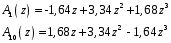 Делим 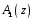 на на 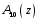 : : 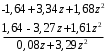 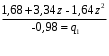 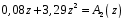 Результаты расчёта показывают, что 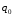 и и 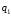 по модулю меньше единицы, что соответствуют условиям устойчивости. Следовательно, цифровая система устойчива. по модулю меньше единицы, что соответствуют условиям устойчивости. Следовательно, цифровая система устойчива. |
