Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич

• Название: Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
• Дата: 14.12.2022
• Размер: 0.49 Mb.
• Имя файла: Диплом Лоренц Степанова.docx
• Тип: Исследование; #844826
• страница: 2 из 11

ВВЕДЕНИЕ

Анализ критериев устойчивости функционирования динамических объектов при наличии априорной неопределенности в пространстве параметров является традиционно своевременным и актуальным направлением научных и производственно-исследовательских задач. Современная система мониторинга и управления обязана адекватно функционировать при подаче возмущающих воздействий самой богатой природы. Указанная особенность динамики связана с таким фундаментальным понятием как устойчивость. Проблеме анализа устойчивости посвящено значительное количество трудов и исследований, поэтому в работе рассмотрен прикладной аспект понятия устойчивости применительно к систем в линейной постановке задач. Устойчивой системой называется та, которая свободно приходит в положение стабильного равновесия после прекращения переходного процесса [3, 5, 8, 9]. В ней регулируемая величина со временем устойчиво асимптотически приближается к постоянному значению. Применение алгебраических и частотных методов исследования качества системы управления обеспечивает безопасную работу наблюдаемого объекта. И хоть при изготовлении и эксплуатации его параметры могут отличаться от расчетных параметров, то всё равно гарантируется их соответствие стабильному поведению диагностируемого объекта.

Целью работы является исследование особенностей анализа устойчивости цифровых систем управления.

Для достижения указанной цели поставлены следующие задачи:

1. 
   Провести обзор литературных источников по вопросам анализа качества математических моделей цифровых систем управления.
   
2. 
   Изучить классификацию состояний устойчивости переходных процессов.
   
3. 
   Рассмотреть особенности и принципы применения алгебраических критериев Рауса, Шур - Кона и Гурвица.
   
4. 
   Исследовать специфику модифицированного критерия устойчивости Льянара - Шипара.
   
5. 
   Провести тестовые расчеты для исследования устойчивости дискретных динамических объектов 3-гo - 5-гo порядков.
   

ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ УСТОЙЧИВОСТИ ЦИФРОВЫХ СИСТЕМ УПРАВЛЕНИЯ

1.1. Определение устойчивости цифровой системы

Устойчивость – это способность системы сохранять текущее состояние при влиянии внешних воздействий или приходить к нему из неравновесного состояния самостоятельно, т.е. без внешних воздействий.

Устойчивость традиционно выступает как одна из ее важнейших свойств. Соблюдение управляемости, наблюдаемости и устойчивости динамики существенно обуславливают возможность функционирования заданных характеристик и особенностей системы в предписанных технологическим процессом эксплуатационных пределах и условиях в установленный временной диапазон. При неустойчивой системе данную задачу управления невозможно решить качественно [6, 7, 9].

Неустойчивость также может привести к незамедлительному прекращению функционирования самой системы в процессе управления или разрушению объекта управления, поэтому использование систем с неустойчивыми переходными характеристиками нецелесообразно.

Отсутствие устойчивости динамических систем управления, в большинстве случаев, возникает из-за очень сильного действия обратной связи. Причинами динамической неустойчивости обычно являются значимо выраженные инерционные характеристики звеньев замкнутой системы, из-за которых сигнал обратной связи в режиме колебаний значительно далек от входного сигнала, что оказывается с ним в фазе. Получается, что характер действия отрицательной обратной связи приобретает признаки положительной [1, 2, 8].

Устойчивость системы является внутренним свойством системы, зависящим только от вида корней характеристического уравнения, описывающего свойства системы, и не зависящим от внешнего воздействия.

Наглядное представление о системах, устойчивых при малых и неустойчивых при больших возмущениях, дает поведение шара во впадине на рисунке 1. При малых воздействиях на шар и его малых отклонениях не выше края впадины шар возвращается в исходное положение и система шар - поверхность устойчива. При больших воздействиях с отклонением за край впадины шар не возвращается в исходное положение - система неустойчива. Поэтому устойчивость систем исследуется отдельно для случая малых и больших возмущений. Проблема устойчивости обычно возникает в замкнутых системах из-за влияния обратной связи. Поэтому в дальнейшем устойчивость исследуется на примерах замкнутых систем, хотя методы исследования устойчивости универсальны [5, 6].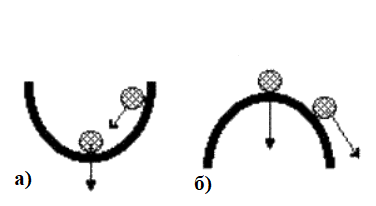



Рис. 1. Структура системы управления: а) устойчивое равновесие, б) неустойчивое равновесие.

При анализе динамических систем управления именно вопрос об устойчивости характеризует свойство системы стабильно работать в нормальных режимах и при воздействии дестабилизирующих факторов. Кроме того, оно является обязательным техническим требованием, от которого напрямую зависят показатели качества и точности системы автоматического управления.

Задача исследования систем на устойчивость может быть поставлена двояко:

1) устойчива ли система при заданном значении её параметров;

2) в каких диапазонах можно изменять параметры системы, не нарушая её устойчивости.

Вторая задача исследования имеет место при наладке и эксплуатации систем автоматического управления.

Основные определения устойчивости дискретных систем справедливы так же, как и для непрерывных систем управления.