Логика. Конспект книги
 Скачать 1.72 Mb. Скачать 1.72 Mb.
|
|
Контрольные работы Контрольная работа по курсу логики по темам “Понятие” и “Суждение” Вариант 1 1. Определить вид следующих понятий: капиталист, остров, кодекс, созвездие Большая медведица. 2. Определить отношения между следующими понятиями: ору дие преступления, пистолет, огнестрельное оружие. 3. Обобщить и ограничить следующие понятия: озеро, сту дент. 4. Определить состав, вид, распределенность терминов в суж дении, записать его кругами Эйлера: “Ни один океан не имеет пресную воду”. 5. Определить, является ли данная формула логическим законом: (a→( 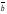 → с)) → ((а ^ → с)) → ((а ^ 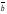 )→ с). )→ с).Вариант 2 1. Определить вид следующих понятий: крестьянин, море, гвардейский полк, нерадивость. 313 2. Определить отношения между следующими понятиями: тре угольник, равнобедренный треугольник, равносторонний тре угольник, прямоугольный треугольник, остроугольный треугольник. 3. Ограничить и обобщить следующие понятия: море, гражданин России. 4. Определить состав, вид, распределенность терминов в суждении, записать их кругами Эйлера: “Не все люди изуча ют логику”, 5. Определить, является ли формула логическим законом: (x→(y^z)) → (( 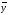 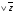 )→ )→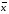 ). ).Контрольная работа по теме “Умозаключение” Вариант 1 1. Привести пример простой деструктивной дилеммы, напи сать ее схему и формулу. 2. Определить вид умозаключения, составить схему и фор мулу. Доказать, является ли формула законом логики: Если человек имеет повышенную температуру, то он болен. Этот человек болен. Этот человек имеет повышенную температуру. 3. Определить правильность категорического силлогизма: Все студенты должны хорошо учиться. Иванов не является студентом. Иванов не должен хорошо учиться. 4. Сделать превращение, обращение и противопоставление предикату: “Некоторые люди не являются грамотными”. 5. Определить вид умозаключения, построить его схему. Все розы - цветы. Все цветы - растения. Все растения дышат. Все розы дышат. Контрольная работа проводится по отдельным карточкам, которые выдаются каждому студенту. Всего подготовлено 8 314 различных вариантов. Остальные 7 аналогичны приведенному выше 1. Доктор философских наук, профессор Б. Л. Яшин, более 15 лет преподающий логику на различных факультетах Московского пе дагогического государственного университета, на индустриально-педагогическом факультете успешно применяет программирован ный контроль за знаниями студентов. Он дает каждому студенту контрольную работу, состоящую из 5 задач (у него их около 30 ва риантов). Студент, выбирая из нескольких предложенных ответов один, с его точки зрения, правильный ответ, отмечает его в виде указанного числа. Таким образом, выполненная студентом конт рольная сводится к перечню выбранных им цифр, что существенно экономит время, которое он тратит на выполнение работы, и облег чает контроль его знаний преподавателю. Итоговой формой контроля за активизацией мыслительной де ятельности студентов в ходе учебного процесса является прове дение зачета или экзамена. Зачет состоит из одного вопроса и одной задачи, подобранных из различных тем, экзамен - из таким же образом отобранных двух вопросов и задачи. На том и другом вывешиваются около 25 наглядных пособий, сделанных в виде таблиц. Делается это с целью, чтобы студенты не старались за учивать формулы символической логики, а четко разбирались в структуре умозаключения, могли проиллюстрировать формулы умозаключений своими (обязательно своими, а не взятыми из учеб ника или лекции) примерами, показать, где и как используются в мышлении, в том числе и в процессе обучения в школе, те или иные логические знания. Хотя отдельные формулировки, - в пер вую очередь, основных законов формальной логики - студенты должны знать твердо и уметь разъяснять их суть. Таким образом, во время сдачи зачета или экзамена упор дела ется не просто на работу памяти, а на активное функционирование всех звеньев мозга учащегося. В. А. Сухомлинский писал по этому поводу: “Умственный труд - это вовсе не всякое сиденье на уроке или дома за книжкой. Зубрежка - не умственный труд, это просто зубрежка. Труд памяти - не умственный труд, умственный труд -усилие мысли, и только это усилие!.. Я стремился... чтобы законы мышления дети осознавали как стройное сооружение, архитектура 315 которого подсказана еще более стройным сооружением - приро дой. Чтобы не превратить ребенка в хранилище знаний, кладо вую истин, правил и формул, надо учить его думать”'. При оценке на экзамене знаний студентов учитывается вся их работа в течение года. Отметка на экзамене складывается из ответа на экзамене, оценок за одну или две контрольные ра боты, текущих оценок, оценок за две-три самостоятельные до машние работы или педпрактику, а также за решение двух за дач с использованием компьютера. В 1988-89 учебном году впервые в ходе зачетов и экзаменов на педфаке при решении задач использовались персональные компьютеры. Сами студен ты педфака, изучившие информатику, написали около 30 про грамм по логике для ЭВМ. Работа в этом направлении продолжа ется. Подобный комплексный подход требует дополнительных времени и усилий преподавателя, но зато позволяет активизиро вать работу студентов и более точно оценивать их знания по курсу логики. В результате систематической работы студентов и столь же систематического контроля за ней оценки на экзаме не в подавляющем большинстве бывают “5” и “4”. (Речь здесь идет о студентах, обучающихся на стационаре, а не о заочниках или вечерниках). Вопросы экзаменационных билетов 1. Формы познания. 2. Понятие о логической форме (структуре) мысли и логиче ском законе. 3. Истинность мысли и формальная правильность рассужде ний. 4. Формальная логика как наука, ее значение в обучении. 5. Семантические категории языка: дескриптивные (описатель ные) термины. 6. Семантические категории языка: логические термины. 7. Понятие как форма мышления. Языковые формы выраже ния понятий. _______________________ 'Сухомлинский В. А. О воспитании. М., 1975. С. 70-71, 88. 316 8. Основные логические приемы формирования понятий: ана лиз, синтез, сравнение, абстрагирование, обобщение. Формирова ние понятий в процессе обучения. 9. Содержание и объем понятия. Закон обратного отношения между объемами и содержаниями понятий. 10. Виды понятий. 11. Отношения между понятиями. 12. Определение (дефиниция) понятия. 13. Приемы, сходные с определением понятий. 14. Деление понятий. 15. Классификация. 16. Ограничение понятий. 17. Обобщение понятий. 18. Общая характеристика суждения. Суждение и предло жение. 19. Виды простых суждений. 20. Категорические суждения и их виды (деление по количест ву и качеству). 21. Распределенность терминов в категорических суждениях. 22. Образование сложных суждений из простых с помощью логических связок: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания. 23. Отрицание суждений. 24. Выражение логических связок (логических постоянных) в естественном языке. 25. Отношения между суждениями по значениям истинности. 26. Деление суждений по модальности. 27. Понятие о логическом законе. 28. Закон тождества, его использование в обучении. 29. Закон непротиворечия, его значение в обучении. 30. Закон исключенного третьего, его использование в обучении. 31. Закон достаточного основания, его роль в обучении. 32. Общее понятие об умозаключении. Понятие логического следования. 33. Обращение и превращение. 34. Противопоставление предикату. 35. Выводы по “логическому квадрату”. 317 36. Категорический силлогизм. Фигуры силлогизма. Cпециальные правила фигур. Модусы категорического силлогизма. 37. Правила категорического силлогизма. 38. Сокращенный категорический силлогизм (энтимема). 39. Прогрессивный полисиллогизм. 40. Регрессивный полисиллогизм. 41. Сориты. 42. Эпихейрема. 43. Прямые выводы. Чисто условные умозаключения. 44. Условно-категорические умозаключения. 45.Разделительные умозаключения. 46. Условно-разделительные (лемматические) умозаключения. Конструктивные дилеммы. 47. Деструктивные дилеммы. 48. Индуктивные умозаключения, их роль в познании. Поня тие вероятности. 49. Полная индукция, ее роль в познании. Понятие о матема тической индукции. 50. Индукция через простое перечисление (популярная). Индукция через анализ и отбор фактов. Условия повышения степени вероятности этих выводов. 51. Научная индукция на основе установления причинной связи. Достоверность ее заключений. 52. Индуктивные методы установления причинных связей. Метод сходства. Метод различия. 53. Индуктивные методы установления причинных связей. Метод сопутствующих изменений. Метод остатков. 54. Умозаключение по аналогии и его виды. Использование аналогий в процессе обучения. 55. Дедукция и индукция в учебном процессе. 56. Понятие аргументации: Структура доказательства. 57. Прямое и косвенное доказательство. 58. Опровержение. Прямой и косвенный способы опровержения. 59. Правила доказательного рассуждения. Ошибки, совершае мые относительно доказываемого тезиса. 60. Правила по отношению к аргументам. Ошибки в основани ях (аргументах) доказательства. 318 61. Софизмы и паралогизмы. Понятие логических парадоксов. 62. Гипотеза как форма развития знаний. Виды гипотез. 63. Построение гипотезы и этапы ее развития. 64. Способы подтверждения и опровержения гипотез. 65. Логическая структура вопроса и ответа. 66. Развитие логического мышления младших школьников. 67. Развитие логического мышления учащихся в средних и старших классах. Необычной и оригинальной формой зачета и даже экза мена является проведение научно-методической конферен ции на английском языке, где студенты овладевают термина ми логики на наиболее распространенном в мире языке научного общения. На педагогическом факультете МПГУ им. В. И. Ле нина (где курс логики составляет 60, а не 40 часов) в 1992,1993 и 1994 годах было проведено шесть таких конференций со сту дентами I курса. Идея приема зачета и экзамена по логике в подобной форме возникла после сдачи экзамена по английскому языку на курсах повышения квалификации в Исследовательском центре проблем качества подготовки специалистов Государственного коми тета Российской Федерации по высшему образованию под ру ководством профессора С. В. Русановой и доцентов Г. Е. Выборовой и К. С. Махмурян, где я дважды проходила обучение. Их методика приема экзамена мною, студентами-первокурсника ми и слушателями факультета общественных профессий (отде ление логики) была развита и творчески воплощена на таких конференциях. Семь-восемь студентов готовили краткие доклады по избран ному разделу тем: “Понятие”, “Умозаключение” или “Роль логи ки в познании и обучении”. Студенты читали доклады, получали вопросы и отвечали на них на английском языке. Материал для выступления они брали из словаря по логике “Logic. Made Simple. A Dictionary”, изданного на английском и испанском языках в из дательстве “Прогресс” соответственно в 1990 и 1991 гг., автора ми которого являются профессора А. Д. Гетманова, М. И. Панов и В. В. Петров. В связи с тем, что ряд студентов изучает французский или не мецкий языки, на нашу конференцию, которая проходила в форме 319 международного конгресса под девизом “Логика на службе; и прогресса”, якобы прибывали научные делегации из Франции и Германии, и доклады студентов были на этих языках (с син хронным переводом на русский). С английского же на русский! язык перевод осуществлялся крайне редко. Эта первая (официальная) часть конгресса позволяла изложить основной логический материал по избранной теме в виде небольших докладов. Вторая часть конгресса (неофициальная) проходила в основном также на английском с привлечением французского, немецкого, иногда испанского или украинского языков. Она состояла из инсценировок, песен, стихотворений, юмористических сценок, танцев, хорового пения и других видов самодеятельного искусства. Все было очень весело преподнесено, оригинально задумано, с хорошим эстетическим вкусом исполнено, вызывало улыбки, смех и аплодисменты. Разыгрывались пантомимы, изображавшие трактовки таких понятий логики, как “умозаключение” и “понятие”, выражалось отношение между понятиями “кошка” и “хвост” (с помощью кругов Эйлера), четыре студен тки изобразили понятие “трикотаж”, другие выразили жестами понятие “электрическая лампочка”. После доклада на тему “Аналогия” студентки показали пантомиму, с помощью которой 3 выразили аналогию между Солнцем и планетами, с одной сто роны, и ядром атома и электронами - с другой. Доклады на тему “Дилемма” сопровождались инсцениров ками, показывающими, каким образом герои литературных про изведений (например, Д. Лондона или романа М. Митчелл “Уне сенные ветрам”) решали свои дилеммы. Исполнялись сценки из мексиканских телесериалов “Моя вторая мама” и “Просто Мария”, отражавшие решение вставших перед героями их лич ных дилемм. Студенты сами готовили соответствующие кос тюмы или брали их напрокат. Если на дилемму подобрать соответствующие примеры из художественной литературы или кинофильмов можно без боль шого труда, то на трилеммы - значительно сложнее. И вот на одном из экзаменов (22 января 1994 г.) студенты поразили и по радовали, когда в ответ на мое предложение привести примеры 320 трилеммы тут же экспромтом сформулировали восемь ситуа ций, отражающих трилемму - сложный выбор из трех альтерна тив (т. е. трех зол) наименьшего зла. Эта часть экзамена (она проходила на русском языке), свидетельствующая о яркой, не обычной концентрации интеллекта и эмоциональных пережива ний за судьбу героев и героинь той или иной трилеммы, принесла большое удовлетворение и мне, и студентам. В ходе второй (неофициальной) части конференции (конгрес са) значительное место отводилось хоровому пению. На англий ском языке исполнялись песни: “Those Evening Bells” (“Вечер ний звон”), “My Bonnie” и другие. Спетая на русском языке польская народная песня “Шла девица за водою” и яркие сту денческие импровизации этой песни вызвали оживление и смех. Песни и стихотворения исполнялись и на других языках (фран цузском, испанском, арабском, немецком, украинском). Оригинальным разделом программы был “прилет юпитерианки” (иногда со своим спутником, иногда без него). Это позволяло отработать материал по логике, посвященной важному разделу “Логическая структура вопроса и ответа”. Задавалось 10-15 вопро сов, на которые следовали иногда серьезные, а иногда юмористи ческие ответы на английском языке. Одежда юпитерианки порою была экстравагантной, необычной - насколько позволяла фанта зия исполнительницы этой роли. Особо следует сказать об оформлении зала. Студенты гото вили самое разнообразное оформление: плакаты, лозунги, мно жество рисунков, тексты стихотворений и песен, эмблемы конгресса - все на английском языке. Рисунки и лозунги в большин стве были взяты из книги Т. Н. Игнатовой “Английский язык (интенсивный курс)” (М., 1992). Там же приведены и ноты к пе сням (с. 18, 43,184). Танцы студенток были выполнены с настоящим и притом вы соким профессионализмом. В общем все студентки и студенты старались проявить свое яркое творческое художественное и му зыкальное дарование. На каждой конференции по два студента (студентки) были ведущими. Они, особенно хорошо владевшие английским язы ком, осуществляли синхронный перевод. Распределение ролей 321 шло на добровольной основе, только по личному желанию, и надо отметить, что иногда желающих было больше, чем требовалось Третья часть - дружеский чай, во время которого звучала музыка и песни, смех и комплименты. Студентки могли продемонстрировать свое кулинарное искусство: испечь к чаю торт, пирожные, печенье, вафли и другие сладости. Моя роль заключалась в том, чтобы в начале конференция. выступить с небольшим докладом на английском языке, предло жить на английском же докладчикам вопросы, на основе картинок сформулировать разделительно-категорические умозаключения (на русском языке), иногда сделать комментарии (тоже на русском), участвовать в хоровом пении на английском и русском языках. В конце выставлялись оценки зачета (экзамена). В подавляющем большинстве они были отличными, редко - хорошими, так как, прежде чем прийти к этому зачету (экзамену) по логике, каждый студент сдавал по 2-3 письменные творческие домашние работы и писал 1 контрольную работу (на 2-часовом семинаре решал 5 задач). Так, например, по теме “Дедуктивные умозаключения”, надо было привести более 25 своих примеров. На конференции присутствовали преподаватели английско го языка и однажды заведующая кафедрой английского языка С. В. Русанова, которые высоко оценили уровень проведения конференции. Такая яркая форма зачета и экзамена запомнится студентам надолго: она позволяет превратить экзамен в праздник, а не в скучный ответ на два вопроса билета и решение задачи, ожида ние которых у студентов зачастую вызывает страх или другие отрицательные эмоции. Кроме того, студенты, став преподава телями, сами смогут провести экзамены в такой же или другой нестандартной форме. Однажды зачет проходил в форме КВН (“Клуб веселых и находчивых”) на русском языке, когда участвовали и соревно вались две команды. Сценарий студенты готовили в основном сами, стараясь мне преподнести сюрприз. И надо отметить, что это им отлично удалось. Студенты группы разделились на две команды, их возглавили капитаны. Форма была такой же, как и в 322 обычном КВНе; этапы соревнования команд оценивались бал лами 3,4 и 5 (оценку производили члены избранного жюри, со стоящего из преподавателей и некоторых студентов группы). Было очень весело, много интересных и забавных находок, за гадок и пантомим предложили студенты своим сокурсникам и нам, трем преподавателям логики, присутствовавшим на этом КВНе. Каждого преподавателя они приветствовали своими сти хами, шутливыми и остроумными. И, наконец, некоторые студенты сдавали экзамен, включаю щий решение логических кроссвордов, а также в форме игры “Мор ской бой”, которую, как и все кроссворды, они придумали сами. Другим интересным способом проверки знаний студентов явля ется работа на ЭВМ. Программу для ЭВМ составил Б. Л. Яшин совместно с преподавателем математики индустриально-педагоги ческого факультета. Ряд предложенных им задач на разные темы курса логики студент должен решить за 20 минут, и машина сама поставит ему оценку за экзамен. Б. Л. Яшин ввел эту форму конт роля знаний студентов с 1993/94 учебного года. Логические кроссворды, придуманные студентами, охваты вали материал либо одной какой-то темы (“Понятие”, “Сужде ние”, “Умозаключение”), либо двух тем (“Суждение” и “Законы правильного мышления”), либо материал всего курса логики. Много интересных, творческих кроссвордов предложили студен ты 1 курса педфака МПГУ. Среди них следует особо отметить три кроссворда, придуманные Обуховой Марией (в 1992 г.), -серьезные, интересные, включающие не только проверку теоре тического материала, но и решение задач. Один из них приво дится ниже. Кроссворд по теме “Понятие” По горизонтали: 2.. Вид отношения, в котором находятся поня тия “школа” и “институт”. 3. Вид данных понятий (отрицательное или положительное): “невыгодная ситуация”, “неинтересный урок”, “безрадостное состояние”. 4. Прием, сходный с определением по нятия, отраженный в этом отрывке из критического этюда И. А. Гон чарова “Мильон терзаний” о Софье Павловне, героине комедии  323 323А. С. Грибоедова “Горе от ума”: “Это - смесь хороших инстинктов с ложью, живого ума с отсутствием всякого намека на идеи и убеждения, путаница понятий, умственная и нравственная слепота -все это не имеет в ней характера личных пороков, а является как общие черты ее круга. В собственной личной ее физиономии прячется в тени что-то свое, горячее, нежное, даже мечтательное. Остальное принадлежит воспитанию”. 6. Вид деления понятий в следующий примерах: “Вирусы бывают ДНК-содержащие и РНК-содержащие” “Цветковые растения делятся на однодольные и двудольные” 7. Логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина. 8. Вид определения понятия в данном примере: “Аутсайдер - термин из зарубежной социальной психологии, обозначающий члена группы, отвергаемого ею по причине психологической несовместимости”. 13. Разновидность неявного определения, позволяющего выяснить содержание незнакомого слова, выражающего понятие, через контекст 14. Вид отношения, в котором находятся понятия “учащийся человек”, “старшеклассник”. 15. Вид понятий, где мыслятся предметы, существование одного из которых предполагает существование другого. По вертикали: 1. Вид понятия, в котором мыслятся пред меты, существующие самостоятельно, вне зависимости от другого предмета. 2. Вид данных понятий (собирательное или несобирательное): “лес”, “Государственная библиотека иностранной 324 литературы”, “созвездие Андромеды”. 3. Одна из логических операций в данном примере: композитор; русский композитор; рус ский композитор и музыкальный критик; русский композитор и музыкальный критик, участник “Могучей кучки”; участник “Мо гучей кучки” Цезарь Антонович Кюи. 5. Вид данных понятий (кон кретное или абстрактное): “благородство”, “различие”, “горечь”. 6. Логическое действие, посредством которого объем исходного понятия (множество) распределяется на ряд подмножеств, исхо дя из выбранного признака. 8. Вид определения понятия, в кото ром место определяющего понятия занимает контекст, или набор аксиом, или описание способа построения определяемого объек та. 9. Вид неявного определения понятия - такого, что определя емый термин используется в выражении понятия, которое ему при писывается в качестве его смысла. 10. Прием, сходный с опреде лением понятия, в данном примере: “Борис и Глеб в истории Руси имеют большее значение не как сыновья Владимира Красного Солнышка, а как первые среди святых русской православной цер кви”. 11. Название сравнимых понятий, объемы которых не сов падают ни в одном элементе. 12. Вид понятия, содержание кото рого можно отнести к каждому предмету данного класса, мысли мого в понятии. Ответы на кроссворд По горизонтали: 2. Соподчинение. 3. Отрицательное. 4. Харак теристика. 6. Дихотомическое. 7. Определение. 8. Номинальное. 13. Контекстуальное. 14. Подчинение. 15. Относительное. По вертикали: 1. Безотносительное. 2. Собирательное. 3. Огра ничение. 5. Абстрактное. 6. Деление. 8. Неявное. 9. Индуктив ное. 10. Различение. 11. Несовместимые. 12. Несобирательное. Постоянный поиск новых форм лекций, семинаров, проведе ния педпрактики, организации внеаудиторной работы со студен тами, форм оценки знания, в том числе зачетов и экзаменов, -показатель творческого подхода к обучению и воспитанию как со стороны преподавателя, так и студентов. 325 Формы внеаудиторной работы со студентами К формам внеаудиторной работы со студентами, в которой участвуют не все, но большинство студентов, изучающих логику на педфаке МПГУ им. В. И. Ленина по 90-часовой программе, относятся следующие: участие студентов в конкурсах студенческих научных работ, кружок по логике, переводы книг а статей по логике с иностранных языков, изготовление студент. ми наглядных пособий по курсу логики, читательские конференции, курсовые и дипломные работы по логике, экспериментальная работа с учащимися в начальной и средней школе, выступление студентов в школе с лекциями по логической тематике другие виды работы. Кратко расскажем о некоторых из них. Участие студентов в конкурсах студенческих научных работ осуществляется ежегодно в течение последних 15 лет. Особенности проведения этой работы: во-первых, ее массовость т. е. охват значительной части студентов, слушающих курс лекций на педагогическом или дошкольном факультетах; во-вторых, представление коллективных работ по одной теме; в-третьих, выделение среди них работ, посвященных развитию логического то мышления школьников, обобщающих эксперименты студентов; в-четвертых, широкое использование в работах аппарата символической логики (как двузначной классической, так и многозначных логик); в-пятых, предварительное знакомство с результатами студенческих работ, представляемых на конкурс, на заседании логического кружка; в-шестых, участие в научных работах иностранных студентов, обучающихся на этих факультетах в МПГУ им. В. И. Ленина. Приведем направления и темы некоторых студенческих ра бот, представленных на конкурсы. 1. Работы, посвященные развитию логического мышления школьников, написаны на такие темы: “К. Д. Ушинский о логике и развитии логического мышления у младших школьников”; “Использование определений, делений, обобщений и ограни чений понятий в школьных учебниках”; “Развитие логическо го мышления детей младшего и среднего школьного возраста”; “Развитие логического мышления школьников в процессе оперирования понятиями”; “Логические ошибки, возникающие 326 при употреблении понятий и в операциях с ними (на материале учебной литературы)”. 2. Работы, отражающие процесс использования курса логики при изучении педагогики и психологии. Темы этих работ: “Педаго гика и логика” и “Логические основы преподавания психологии”. 3. Коллективные или индивидуальные работы, написанные с использованием аппарата символической логики: “Формализация трилеммы”, “Роль условно-категорических умозаключений в по знании”, “Формализация эпихейремы”, “Формализация раздели тельных умозаключений”, “Полисиллогизмы и сориты в классиче ской и многозначных логиках”, “Правила приведения к абсурду в двузначной и многозначных логиках”, “Формализация полисилло гизмов и соритов с общими посылками”, “Закон исключенного третьего”, “Дилемма в классической и многозначных логиках”. Доказательство формул в двузначной логике производилось тре мя способами: приведением формулы к конъюнктивной нормаль ной форме, методом построения таблиц (матриц), с использова нием правил натурального вывода. 4. Работы иностранных студентов на темы: “Логические свя зки и их применение в немецком языке” (студентки из Герма нии), “Выражение логических терминов в чешском языке” (студентки из Чехии), “Выражение логических связок в болгарском языке” (студентки из Болгарии). Так, студентка из Венгрии первой перевела на русский язык отдельные части книги венгерского логика Каталины Хаваш “Так логично!”. (Позднее эта книга была издана на русском языке издательством “Прогресс” в профессиональном переводе). К переводу студентка приложила очень интересную логическую игру, ходы в которой осуществляются с помощью фишек разли чных цветов. “Так логично!” адресована старшеклассникам и поэтому написана в популярной, занимательной форме, в ней много логических игр, логических задач и другого наглядного материала. Автор Каталина Хаваш, ознакомившись с перево дом студентки, отметила его достаточно высокий уровень. А студентка из Болгарии со своей сокурсницей из России сде лала совместный перевод с болгарского на русский язык учебни ка по логике для учащихся средней школы, изданного в Софии в 1980г. 327 Следует отметить, что иностранные студенты добросовестно занимаются изучением логики, с большим интересом, часто по своей инициативе выполняют дополнительные работы, связанные с углубленным изучением курса логики. 5. Работы студентов написаны на различные темы, способствующие углубленному изучению отдельных разделов курса логик “Доказательства и ошибки в полемике”, “Математические софизмы”, “Выражение логических связок в произведениях А. Н. Островского и М. Шолохова (сопоставительный анализ)”, “Среде выражения отрицания (по произведениям А. И. Герцена)”, “Дилеммы и трилеммы в художественной литературе и искусстве”, “Сориты Кэрролла” и многие другие темы. Важной формой внеаудиторной работы является участие студентов в работе кружка по логике. Кружок по логике в течение 18 лет ежемесячно проводит свои заседания в студенческом общежитии педагогического факультета МПГУ. Работа кружка прежде всего направлена на углубление и расширение знаний студентов, ориентирование на их творческое отношение к курсу философских наук. На заседаниях кружка изучались такие темы: “Роль логики в познании”, “Развитие логического мышления, процессе обучения в школе - на уроках истории и математики” “Проблемное обучение”, “Роль логики в работе следователя”, “О чувстве юмора и остроумии”, “Как познают мир слепоглухонемые”, “О приметах верных и суеверных”, “О культуре поведения” и др. В работе кружка и по внеклассной работе со студентами можно использовать такие формы, как читательские конференции. К внеаудиторной работе по логике относится написание кур совых и дипломных работ по логике. Дипломные работы написаны по таким темам: “Проблемы отрицания в психологии и логике”, “Развитие логического мышления школьников младшего возраста в процессе оперирования понятиями” и др. Темы курсо вых работ по логике значительно многообразнее. Два студента исторического факультета под руководством доктора философских наук Г. В. Сориной в течение года подготовили курсовые работы по логике на тему: “Логический анализ диалогов Платона” и высту пили с сообщением на Международной научно-теоретической конференции “Познание и его возможности” (Москва, 1994). 328 Студенты педагогического факультета и факультетов началь ных классов и дошкольного воспитания сами или с привлечением художников изготовили более 30 наглядных пособий по логике, что облегчает проведение лекций, семинаров, зачетов и экзаменов. Все шире проводится экспериментальная работа по логике с учащимися начальных, средних и старших классов, которую сту денты осуществляют либо в период непрерывной педпрактики на IV курсе, либо в ходе педпрактики на II курсе педфака. Эта работа проводится по материалам тем “Понятие”, “Суждение” и “Умозаключение”. (Разработки приведены в конце данной методической главы). Указанные многообразные формы внеаудиторной работы со студентами были использованы в течение моего многолетнего преподавания логики студентам перечисленных факультетов МПГУ им. В. И. Ленина и доказали свою полезность и эффек тивность. Преподавание логики ведется в тесной взаимосвязи с педагоги кой и психологией. Как уже упоминалось, на педфаке проведены две теоретические конференции на темы: “Логика и педагогика” и “Психология и логика”, на которых ряд студентов выступили с обстоятельными докладами и представили студенческие науч ные работы по этим темам. Взаимосвязь логики с методиками преподавания отдельных предметов осуществляется в процессе преподавания курса логики на факультетах, а также показана в моем учебнике для педвузов (1986 г.). Широко используются высказывания К. Д. Ушинского, В. А. Сухомлинского, А. С. Ма каренко (употреблявшего понятие “педагогическая логика”) и дру гих видных педагогов и ученых (О. Ю. Богдановой, М. Р. Львова, В. А. Крутецкого, И. Я. Лернера, А. Я. Хинчина). В связи с тем, что в России логика в последние 2-3 года стала преподаваться в отдельных школах с дифференцированным обуче нием, в гимназиях и лицеях, а преподаватели логики почти не го товятся ни в университетах (в том числе - в педагогических уни верситетах), ни в педвузах, встает актуальная проблема орга низации подготовки преподавателей логики для средних учебных заведений, т. е. подготовки студентов по специальности “Логи ка”. Отметим, что пока такой специализации в педвузе нет, но 329 надеемся, что она в ближайшее время будет введена, по ней мере, в МПГУ и Российском педагогическом университете (бывшем Ленинградском пединституте). Итак, связь теории с практикой, соединение логических знаний, полученных студентами в педвузе, и практическое преподавание отдельных разделов курса логики (понятий, суждений и умозаключений) школьникам и учащимся педучилищ поможет активному творческому овладению вузовским курсом логики” Ориентиры теста, позволяющего судить об уровне усвоения студентами основных логических понятий1 1. В школьных учебниках по избранной студентами специальности найти различные виды определения понятий (номинальные, реальные, генетические и др.) и ответить на вопрос: “Правильно ли дано определение понятия?” К сожалению, в школьных учебниках в определении понятий иногда встречаются логические ошибки. Будущий учитель должен уметь исправлять неправильные определения. 2. С помощью кругов Эйлера установить отношения между 4-5 понятиями. 3. В школьных учебниках по специальности найти различные виды деления понятий или их классификацию. Уметь отличить правильно выполненное деление (или классификацию) от неправильно выполненного, найти логическую ошибку (ошибки) и уметь их исправить. 4. Студенты, прослушавшие курс логики, должны уметь рабо тать с умозаключениями: отличить правильно построенное умозак лючение от неправильно построенного; иллюстрировать различные виды умозаключений своими примерами или самостоятельно подобранными примерами из художественной литературы. . 5. Студенты должны овладеть приемами обнаружения разнооб разных логических ошибок, встречающихся в мышлении, уметь исправить эти ошибки. _____________________ 'Программа, ключевые понятия и имена, тесты по курсу логики также даны в книге “Философские дисциплины: программы, требования, методические ре комендации”. М., 1993. С. 25-36. (Авторы А. Д. Гетманова и И. Н. Грифцова). 330 6. Студенты должны научиться корректно, логически грамотно вести диспуты, полемику, дискуссии, быть готовыми обучить этому своих питомцев. Как оптимально соединить преподавание философской логи ки с элементами символической логики? Это не простой вопрос. Некоторые преподаватели логики вместо общей философской логики излагают только математическую (символическую) ло гику примерно в таком виде, каком она читается на математи ческом факультете как математическая дисциплина. Они пре небрегают примерами из конкретных наук и философии, дают чисто символическое изложение. В пединститутах такое изло жение принципиально неприемлемо в курсе философской логики, целью которой является развитие содержательного логического мышления студентов, а через них учащихся школы. Философия и логика являются мировоззренческими, социально-гуманитар ными науками, они должны быть тесно взаимосвязаны с жиз нью, наполнены конкретным содержанием (примерами) из раз ных наук (общественных, естественных, технических), практики (для пединститутов - педагогической), выполнять воспитатель ную функцию. Программа по логике (1996 г.) построена на изложении мате риала традиционной логики с элементами символической логики, предусматривает содержательное изложение логического мате риала, а не изложение только математической логики. Некоторые логики, к сожалению, поступают иначе, подменяя философию ма тематикой, что недопустимо. К тому же они хотели бы, чтобы преподающие логику в пединститутах делали то же самое. Но это в принципе невозможно, не нужно для студентов-педагогов, тем более что курс логики всего 40-часовой или 54-часовой. В пединститутах используются многообразные формы рабо ты (о чем было сказано выше). Для тех же, кто преподает символическую логику, основное в работе - доска, исписанная символами. И тогда легко обойти связь с жизнью, с современно стью, с профилем вуза, с будущей специальностью. Легко уйти из жизни в символику. Но студентам не импонирует такое препо давание логики. Преподавание содержательной, философской логики в пед вузе должно быть взаимосвязано с преподаванием философии, 331 этики, эстетики, педагогики, психологии, информатики и других конкретных наук (истории, астрономии, физики, химии, математи ки), а также с методиками школьного обучения, чтобы дать ло гические основы для преподавания этих дисциплин в педаго гических университетах и педвузах и осуществления педагогической практики. Так, на социологическом факультете доктором философских наук Г. В. Сориной и кандидатом философских наук, доцентом И. Н. Грифцовой, читался авторский курс логики, учи тывающий особенности работы социологов. Итак, существуют два различных подхода к логике и ее пре подаванию. Поэтому хотелось бы предостеречь преподавате лей логики педвузов от одностороннего увлечения преподавани ем символической логики, особенно в современный период, когда результаты диалога во многом зависят от “логической школы” всех заинтересованных сторон, от уровня культуры мышления каждого человека. |
