лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Основные понятия и определения теории дифференциальных уравнений.1. Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию yи ее производные или дифференциалы. 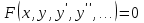 Порядком дифференциального уравнения называется порядок старшей производной, входящей в него. Пример. 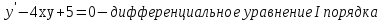 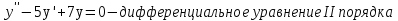 Решением дифференциального уравнения называется функция, обращающая его в тождество. Общим решением дифференциального уравнения называется решение, содержащее столько произвольных постоянных C, каков порядок дифференциального уравнения. 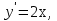 так как 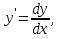 то 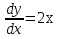 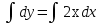 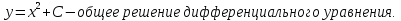 Частное решение дифференциального уравнения получается из общего решения при определенных начальных значениях независимой переменной и искомой функции. Задача нахождения частного решения дифференциального уравнения называется задачей Каши. Геометрическиобщее решение дифференциального уравнения представляет собой семейство интегральных кривых; частное решение ‒ единственная кривая, проходящая через данную точку  . .Дифференциальные уравнения с разделяющимися переменными.Это дифференциальные уравнения вида: 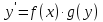 или 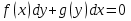 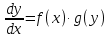 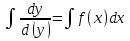 Проинтегрировав, найдем y. Пример. 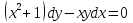 Решение: 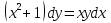 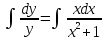 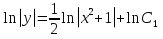 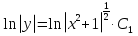 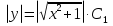 Пусть 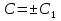 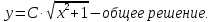 Однородные дифференциальные уравнения первого порядка.Это дифференциальные уравнения вида: 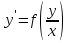 Решается заменой 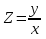 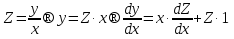 Подставим в исходное уравнение 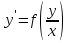 , получим , получим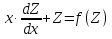 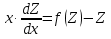 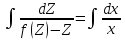 Проинтегрировав, найдем функцию Z, а затем функцию y. Пример. 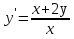 Решение: 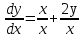 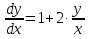 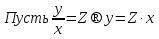 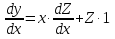 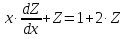 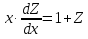 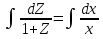 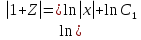 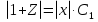 Пусть 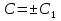 Тогда 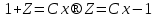 , так как , так как 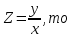 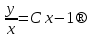  |
