лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Лекция 9.ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ.Рациональной дробью называется отношение двух многочленов 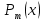 ‒ степени mи ‒ степени mи 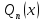 ‒ степениn, ‒ степениn,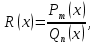 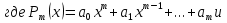 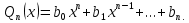 Возможны следующие случаи: 1. Если 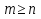 , то применяют метод деления углом для исключения целой части. , то применяют метод деления углом для исключения целой части.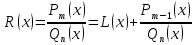 2. Если 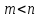 и в знаменателе квадратный трехчлен и в знаменателе квадратный трехчлен 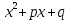 , то применяют метод дополнения до полного квадрата. , то применяют метод дополнения до полного квадрата. 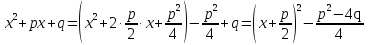 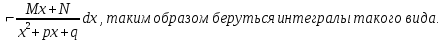 Пример 1. 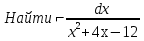 Решение: 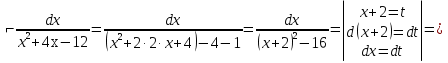 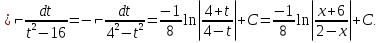 Пример 2. 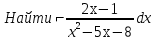 Решение: 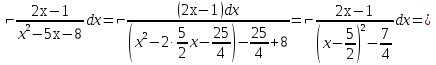 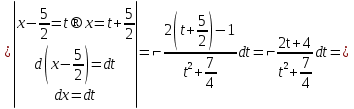 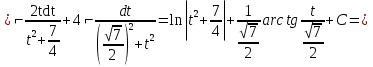 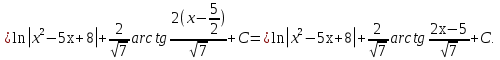 3. Метод неопределенных коэффициентов при разложении правильной рациональной дроби на сумму простейших дробей. Любую правильную рациональную дробь 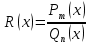 , где , где 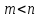 , можно представить в виде суммы простейших дробей: , можно представить в виде суммы простейших дробей: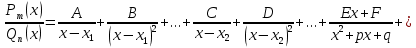 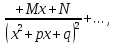 гдеA, B, C, D, E, F, M, N,… ‒ неопределенные коэффициенты. Для нахождения неопределенных коэффициентов надо правую часть привести к общему знаменателю. Так как знаменатель 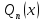 совпадает со знаменателем дроби правой части, то их можно отбросить и прировнять числители. Затем, приравнивая коэффициенты при одинаковых степенях xв левой и правой частях, получим систему линейных уравнений с n‒ неизвестными. Решив эту систему, найдем искомые коэффициенты A, B, C, D и так далее. А,следовательно, разложим правильную рациональную дробь на простейшие дроби. совпадает со знаменателем дроби правой части, то их можно отбросить и прировнять числители. Затем, приравнивая коэффициенты при одинаковых степенях xв левой и правой частях, получим систему линейных уравнений с n‒ неизвестными. Решив эту систему, найдем искомые коэффициенты A, B, C, D и так далее. А,следовательно, разложим правильную рациональную дробь на простейшие дроби. Рассмотрим на примерах возможные варианты: 1. Если множители знаменателя линейны и различны: 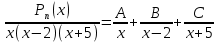 2. Еслисреди множителей знаменателя есть краткие множители: 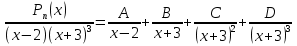 3. Если среди множителей знаменателя есть квадратный трехчлен, неразложимый на множители: 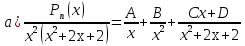 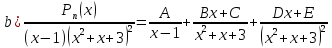 Примеры: Разложить на сумму простейших рациональную дробь. Проинтегрировать. Пример1. 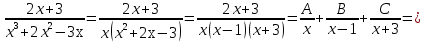 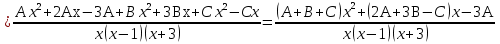 Так как знаменатели дробей равны, то должны быть равны и числители, т. е. 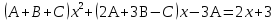 Далее сравниваем коэффициенты при одинаковых степенях xв левой и правой частях. Получаем систему: 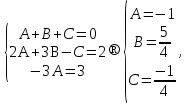 значит 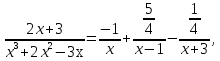 поэтому 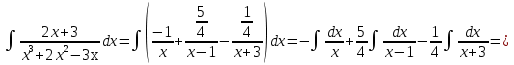 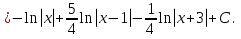 Пример 2. 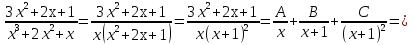 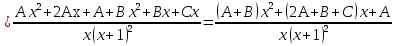 Отсюда 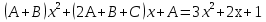 Значит 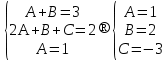 Поэтому 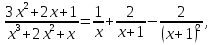 тогда 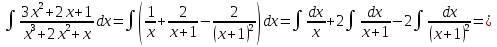 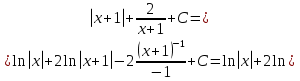 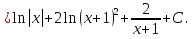 Пример 3. 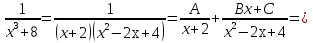 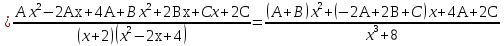 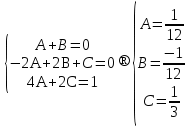 Значит 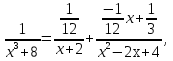 тогда 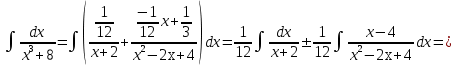 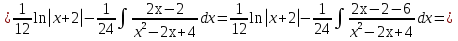 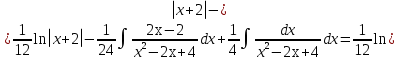 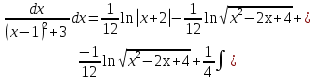 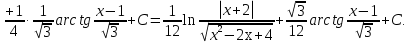 |
