лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Лекция 18. ЧИСЛОВЫЕ РЯДЫ.СУММА РЯДА.Задача суммирования множества слагаемых решается в теории рядов. 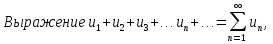 где u1,u2,u3…., un…–члены бесконечной числовой последовательности, называется числовым рядом. Числа u1,u2,u3…., un… называют членами ряда, а un– общий член ряда. Сумма конечного числа n первых членов ряда называется n–й частичной суммой ряда. Sn= u1 + u2 +… + un, т.е. S1= u1; S2= u1+ u2 Sn= u1+ u2+…+ un Ряд называется сходящимся, если существует конечный предел частичной суммы Snпри n 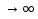 , то есть , то есть 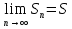 Число S называется суммой ряда. В противном случае: 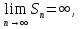 Тогда ряд называется расходящимся. Эталонные ряды. 1. Геометрический ряд (геометрическая прогрессия) 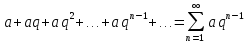 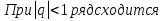 . . . .Пример. 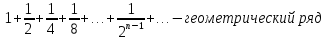 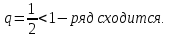 2. Гармонический ряд. 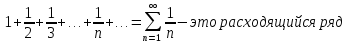 3. Обобщенный гармонический ряд. 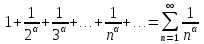 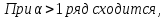 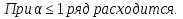 Пример. 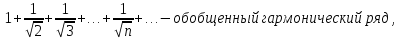 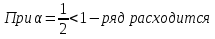 . .Признаки сходимости знакоположительных рядов Теорема 1. Необходимый признак сходимости. 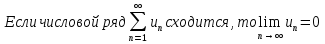 C помощью этого признака можно установить расходимость ряда. Пример. 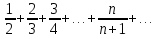 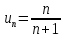 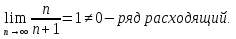 Достаточные признаки Теорема 1.Признак сравнения рядов. Пусть даны два знакоположительных ряда: 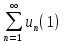 и 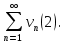 Причем 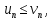 тогда, если ряд (2) сходится, то сходится и ряд (1). тогда, если ряд (2) сходится, то сходится и ряд (1).Если ряд (1) расходится, то расходится и ряд (2). Пример. 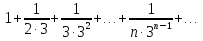 Сравним этот ряд с геометрическим рядом: 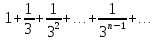 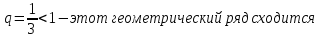 Сравним ряды: 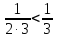 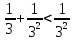 Следовательно, по признаку сравнения искомый ряд сходится. Теорема 2. Признак Даламбера. 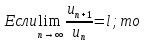
Пример.Исследовать на сходимость ряд: 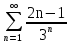 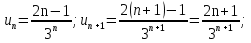 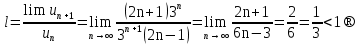  по признаку Даламберу ряд сходится. по признаку Даламберу ряд сходится.Теорема 3.Радикальный признак Коши. 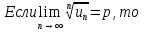 1) при 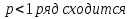 2) при 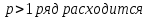 3) при 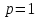 вопрос о сходимости остается открытым. вопрос о сходимости остается открытым.Пример: исследовать на сходимость числовой ряд: 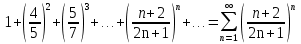 Решение: 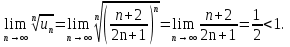 Следовательно, ряд сходится по Коши. Теорема 4. Интегральный признак Коши. Пусть члены ряда 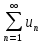 положительны и не возрастают, то есть 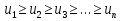 и являются значениями непрерывной невозрастающей функции f(x) при x= 1, 2, …, n. и являются значениями непрерывной невозрастающей функции f(x) при x= 1, 2, …, n.Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл: 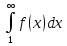 Пример. 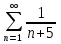 Решение: 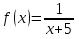 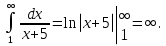 Следовательно, ряд расходится, так как расходится несобственный интеграл. Лекция 19. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ. ПОНЯТИЕ АБСОЛЮТНОЙ И УСЛОВНОЙ СХОДИМОСТИ ЗНАКОПЕРЕМЕНОГО РЯДА.Ряд называется знакопеременным, если любой его член может быть, как положительным, так и отрицательным. Рассмотрим знакочередующиеся ряды: 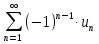 Теорема 1. Признак Лейбница (достаточный признак). Если у знакочередующегося ряда 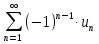 члены убывают по абсолютной величине, то есть 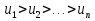 и и 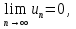 то ряд сходится, и его сумма не превосходит первого члена, то есть S≤ 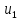 . .Пример. 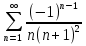 Решение: Применим признак Лейбница: 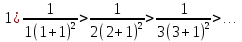 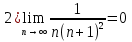 Следовательно, ряд сходится по Лейбницу. Теорема 2. Достаточный признак сходимости знакопеременного ряда. Если для знакопеременного ряда сходится ряд, составленный из абсолютных величин его членов 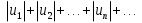 , то данный знакопеременный ряд сходится. , то данный знакопеременный ряд сходится.Пример: исследовать ряд на сходимость: 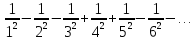 Решение: 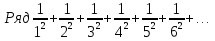 из абсолютных величин членов исходного ряда сходится, как обобщенный гармонический ряд при 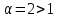 . .Следовательно, исходный ряд сходится. Этот признак является достаточным, но не необходимым, то есть существуют знакопеременные ряды, которые сходятся, хотя ряды, составленные из абсолютных величин, расходятся. Определение 1. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Определение 2.Знакопеременный ряд называется условно сходящимся, если сам рядсходится, а ряд, составленный из абсолютных величин его членов, расходится. Отличие между ними в том, что абсолютно сходящийся ряд сходится из-за того, что его члены быстро убывают, а условно сходящийся ряд сходится из-за того, что положительные и отрицательные члены уничтожают друг друга. Пример. 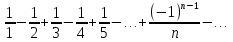 Решение: Применим признак Лейбница: 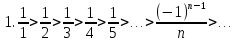 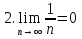 Следовательно, ряд сходится по Лейбницу. Но ряд составленный из абсолютных величин его членов расходится, как гармонический. Значит, исходный ряд сходится условно. Лекция 20. СТЕПЕННЫЕ РЯДЫ. ОБЛАСТЬ СХОДИМОСТИ. ТЕОРЕМА Н. АБЕЛЯ.Перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции. Определение 1. Степенным рядом называется ряд вида: 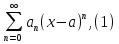 где aи коэффициенты а0,… ,аn – постоянный. При а=0 степенной ряд примет вид: 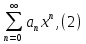 Определение 2.Совокупность значений x, при которых степенной ряд сходится, называется областью сходимостью степенного ряда. Пример. Найти область сходимости. 1+x+ x2 + … + xn +… Это геометрический рядq = x. Он сходится при 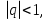 то есть при то есть при 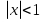 или или 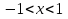 следовательно, область сходимости (−1; 1). следовательно, область сходимости (−1; 1).Структура области сходимости степенного ряда устанавливается с помощью теоремы Н. Абеля: 1. Если степенной ряд (2) сходится приx = x0≠ 0, то он абсолютно сходится и при всех значениях x, удовлетворяет неравенству 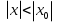 . .2. Если степенной ряд (2) расходится приx = x1≠ 0, то он расходится и при всех значениях x, удовлетворяет неравенству 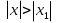 . .Из теоремы Н. Абеля следует, что существует такое число R ≥ 0, что при всех 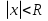 ряд (2) сходится, а при ряд (2) сходится, а при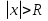 расходится. расходится.Число Rназывается радиусом сходимости степенного ряда, а интервал (−R; R) называется интервалом сходимости. На концах интервала сходимости ряд (2) может, как сходится, так и расходится. Для ряда (1) получим: 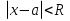 , то есть , то есть 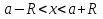 .Следовательно, интервал сходимости ряда (1) имеет вид: .Следовательно, интервал сходимости ряда (1) имеет вид: 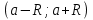 . .Радиус сходимости степенного ряда находится по формуле: 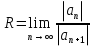 Пример 1. 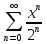 Решение: 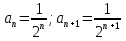 Тогда 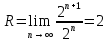 Следовательно, (−2; 2) – интервал сходимости. При 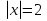 ряд расходится, так как ряд расходится, так как 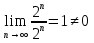 То есть 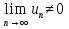 Следовательно,при 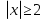 ряд расходится. ряд расходится.Пример 2. 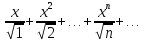 Решение: 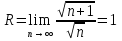 Тогда (−1;1) – интервал сходимости. При x=1ряд расходится, как обобщенный гармонический. При x=−1 получим знакочередующийся ряд. 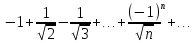 На основании признака Лейбница он сходится, т.к. 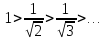 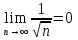 Следовательно, область сходимости −1≤x˂1 Свойства степенных рядов Пусть степенной ряд 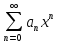 имеет интервал сходимости 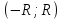 . . Тогдаряд, полученный из данного ряда почленным дифференцированием или интегрированием, имеет тот же интервал сходимости. Следовательно, на интервале сходимости степенные ряды можно почленно дифференцировать и интегрировать. Ряд Маклорена. Ряд Тейлора. Если функция 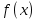 разлагается в степенной ряд по степеням разлагается в степенной ряд по степеням 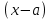 , то ряд имеет следующий вид: , то ряд имеет следующий вид: 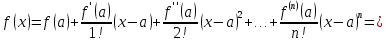 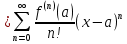 Этот ряд называется рядом Тейлора. В частном случае при a=0 ряд примет вид: 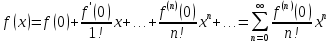 Этот ряд называется рядом Маклорена. Разложение в степенные ряды элементарных функций 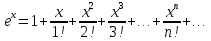 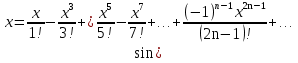 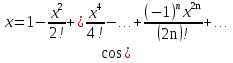 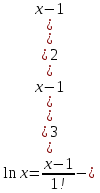 |

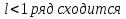
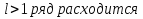
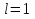 вопрос о сходимости остается открытым.
вопрос о сходимости остается открытым.