лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Лекция 17.ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И ПРАВОЙ ЧАСТЬЮ СПЕЦИАЛЬНОГО ВИДА.Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами: 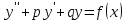 Теорема. Общее решение неоднородного дифференциального уравнения 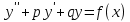 равняется сумме общего решения соответствующего однородного дифференциального уравненияyи частного решения неоднородного уравнения. равняется сумме общего решения соответствующего однородного дифференциального уравненияyи частного решения неоднородного уравнения.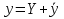 Для дифференциального уравнения второго порядка, у которого правая часть имеет специальный вид, применяются методы подбора формы записи частного решения 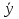 по виду по виду 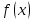 ,а затем метод неопределенных коэффициентов. ,а затем метод неопределенных коэффициентов.Возможны следующие виды 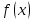 : :1. Если 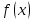 многочлен n ‒ й степени. многочлен n ‒ й степени.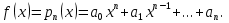 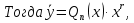 где 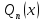 ‒ многочлен, той же степени, что и ‒ многочлен, той же степени, что и 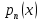 , но с неопределенными коэффициентами (A, B, C, D…), r‒ число корней характеристического уравнения, равных нулю, то есть r= 0, илиr= 1, илиr= 2. , но с неопределенными коэффициентами (A, B, C, D…), r‒ число корней характеристического уравнения, равных нулю, то есть r= 0, илиr= 1, илиr= 2.Пример. 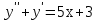 Решение: 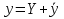 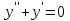 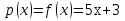 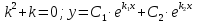 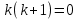 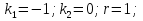 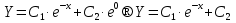 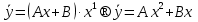 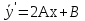 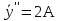 Подставим в исходное уравнение. 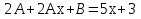 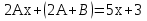 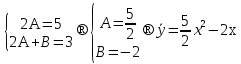 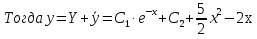 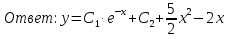 2. Если правая часть уравнения 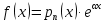 , где α ‒ любое число, тогда , где α ‒ любое число, тогда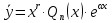 , где r ‒ число корней характеристического уравнения, равных α, то есть r= 0, илиr= 1, илиr= 2. , где r ‒ число корней характеристического уравнения, равных α, то есть r= 0, илиr= 1, илиr= 2.В частном случае 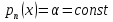 , то , то 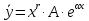 , где A‒неопределенный коэффициент. , где A‒неопределенный коэффициент.Пример. 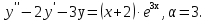 Решение: 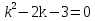 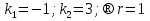 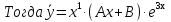 3. Если 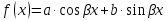 , aиb‒ действительные числа. , aиb‒ действительные числа.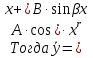 ,где r ‒ число корней характеристического уравнения, совпадающих с ,где r ‒ число корней характеристического уравнения, совпадающих с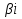 (если D< 0) и r= 0(если D≥ 0). (если D< 0) и r= 0(если D≥ 0).Пример. 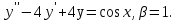 Решение: 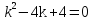 D= 0 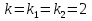 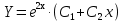 Ответ: 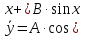 . . |
