|
|
лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
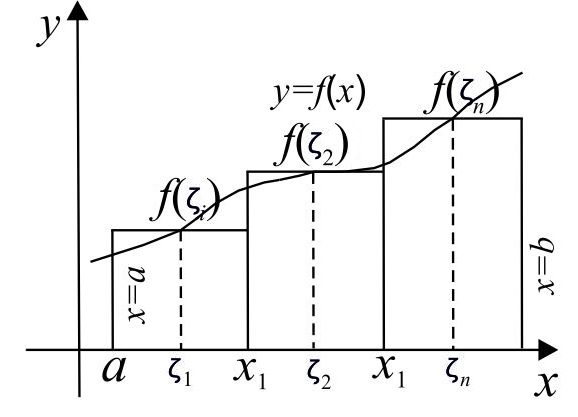
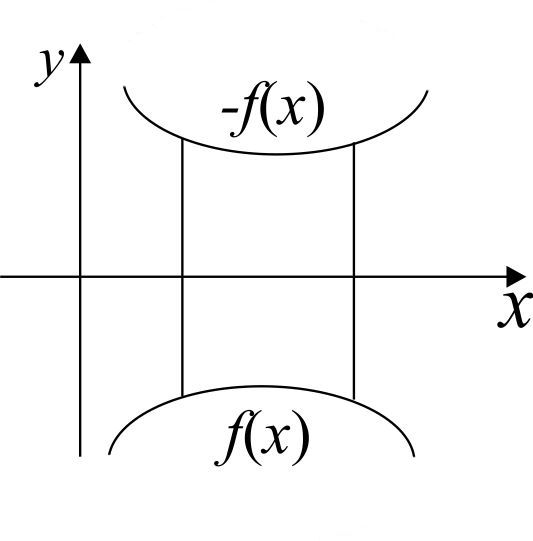
Рис. 1
Определенный интеграл, как предел интегральной суммы.
Геометрический смысл определенного интеграла.
Определенным интегралом от функции f (x) на промежутке [a; b] называется предел интегральной суммы(1).
Геометрический смысл.
Определенный интеграл от непрерывной неотрицательной функции
f(x) на промежутке [a; b] численно равен площади соответствующей криволинейной трапеции:
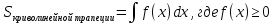
Геометрические приложения определенного интеграла.
1. Вычисление Sфигуры.
1) Если геометрическая фигура ограничена графиками двух непрерывных неотрицательных функций 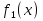 и и 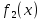 . .
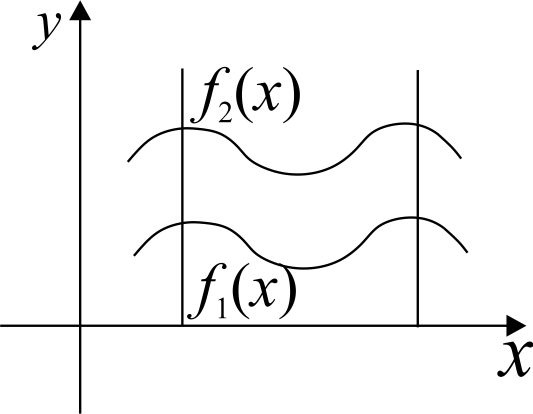
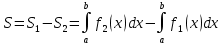
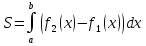
2) Если геометрическая фигура ограничена графиком 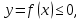
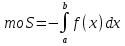
3) Если 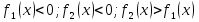
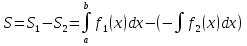
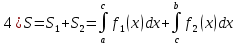
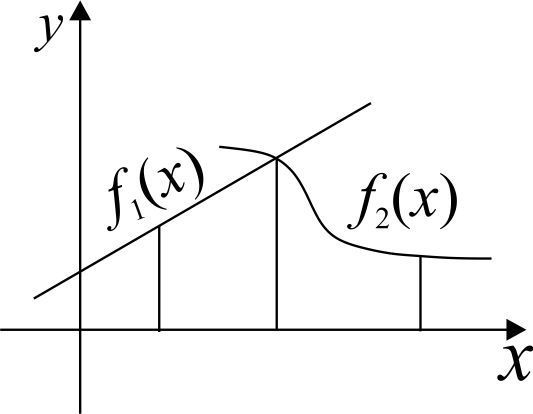
Пример.
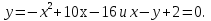
Решение:
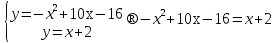
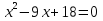
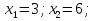
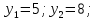
(3; 5), (6; 8) ‒ точки пересечения линии.
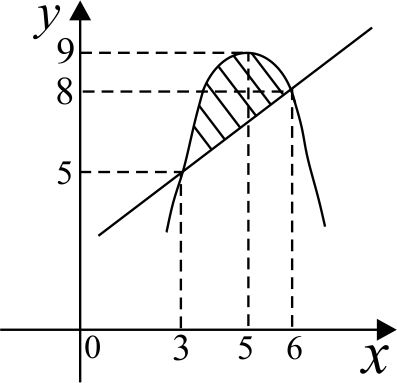
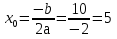
Второйспособ:
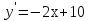
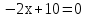
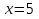
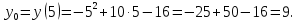
(5; 9) ‒ вершина параболы.
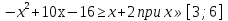
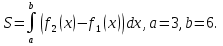
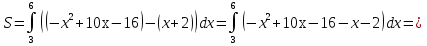
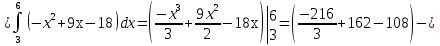
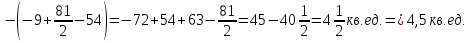
Лекция 13. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
.
Задачи, приводящие к дифференциальным уравнениям.
1. Задача о нахождении закона движения материальной точки.
Обозначив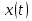 ‒ путь в момент времени ‒ путь в момент времени 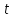 , , 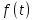 ‒скорость, тогда из физического смысла производной следует, что ‒скорость, тогда из физического смысла производной следует, что
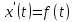
или
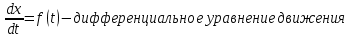
Если 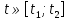 , то получим , то получим 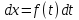 , проинтегрировав это равенство, получим закон движения: , проинтегрировав это равенство, получим закон движения:
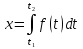
2. Задача о размножении бактерий.
Пусть 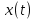 ‒ число бактерий в момент времени ‒ число бактерий в момент времени 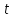 .Так как скорость размножения бактерий пропорциональна их количеству, то по аналогии с предыдущим. .Так как скорость размножения бактерий пропорциональна их количеству, то по аналогии с предыдущим.
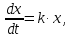
где 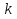 ‒ коэффициент пропорциональности. ‒ коэффициент пропорциональности.
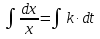
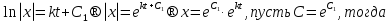
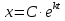
|
|
|
 Скачать 12.08 Mb.
Скачать 12.08 Mb.