лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Лекция 11.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА ‒ ЛЕЙБНИЦА.Определенным интегралом от функции f(x)на промежутке[a;b] называется приращение первообразной функции F(x) при изменении аргумента от x = aдо x = b. Обозначается 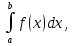 где a ‒ нижний предел интегрирования, а b‒верхний предел интегрирования. Из определения следует: 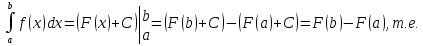 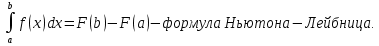 Пример. 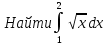 Решение: 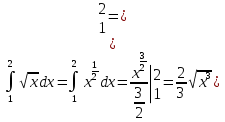 Свойства определенного интеграла.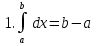 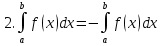 3. Если функции y = f(x)иy = g(x) интегрируемы на отрезке[a, b], то 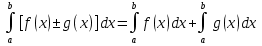 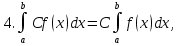 то есть постоянный множитель можно вынести за знак определенного интеграла. 5. Если 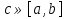 , то , то 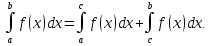 Приемы вычисления определенного интеграла такие же, как и неопределенного интеграла. Метод замены переменной в определенном интеграле.При выполнении замены переменной в определенном интеграле надо:1. под знаком интеграла заменить старую переменную на новую; 2. пересчитать пределы интегрирования. Пример 1. 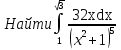 Решение: 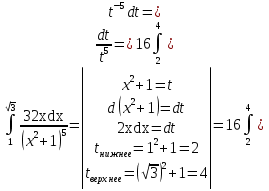 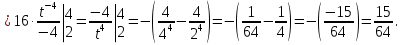 Пример 2. 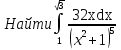 Решение: 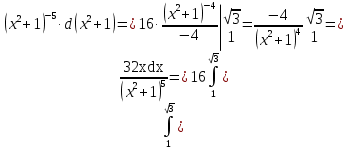 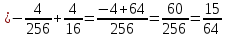 Интегрирование по частям в определенном интеграле.Воспользовавшись формулой интегрирования по частям в неопределенном интеграле 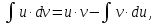 получим формулу интегрирования по частям в определенном интеграле.Которая примет вид: 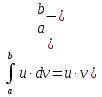 Пример1. 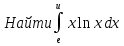 Решение: 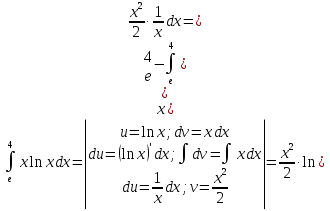 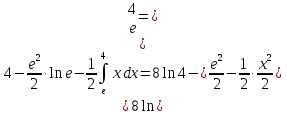 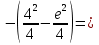 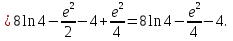 Пример 2. 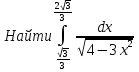 Решение: 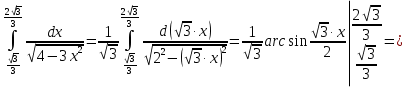 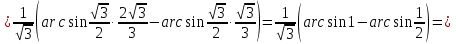 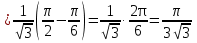 Лекция 12.КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ, КАК ПРЕДЕЛ ИНТЕГРАЛЬНОЙ СУММЫ.ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.Криволинейной трапецией называется геометрическая фигура,ограниченная графиком непрерывной неотрицательной функции y = f (x), отрезками прямых x = a иx = bи отрезком [a; b] осиOX. Разобьем отрезок [a; b] на n‒ отрезков точками 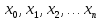 . На каждом отрезке . На каждом отрезке 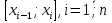 выбираем точку выбираем точку 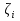 (кси), (кси), 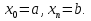 Построим прямоугольники с основанием: 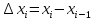 и высотой и высотой f( 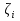 ), тогда ), тогда 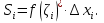 Сумма Сумма 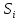 называется интегральной суммой. называется интегральной суммой. 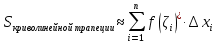 при 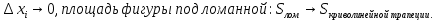 Получим: Получим: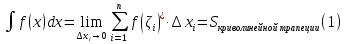 |
