лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Элементы теории множеств. Операции над множествами.Определение 1.Множеством называется совокупность некоторых объектов, объединенных в одно целое по какому ‒ либо признаку. Объекты, из которых состоит множество, называются его элементами. Обозначаются заглавными буквами латинского алфавита A, B, …, X, Y, …, а их элементы обозначаются малыми буквами a, b, …, x, y. Определение 1.1.Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø. Множество можно задать пересечением и описанием. Пример: 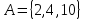 ; ; 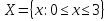 . .Определение 1.2.Множеством Aназывается подмножеством B, если каждый элемент множества A является элементом множестваB. Символически это обозначают так: A 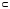 B(A содержится вB). B(A содержится вB).Определение 1.3.Два множества A иB называются равными, если они состоят из одних и тех же элементов (A =B). Операции над множествами. Определение 1.4.Объединением или суммой множеств A иB называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение множеств обозначаютA 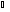 B(или A +B). Кратко можно записать A B(или A +B). Кратко можно записать A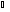 B = B = 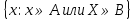 . .A 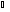 B= A +B B= A +BЕслиB 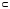 A, тоA +B=A A, тоA +B=A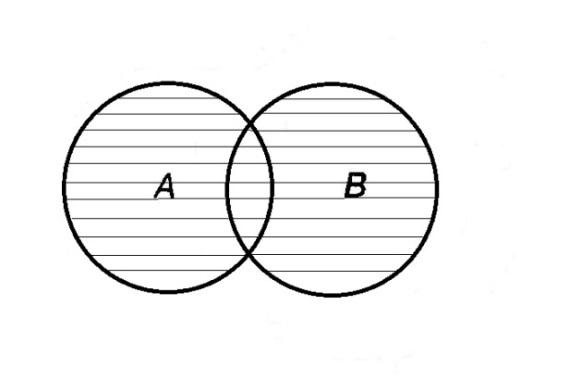 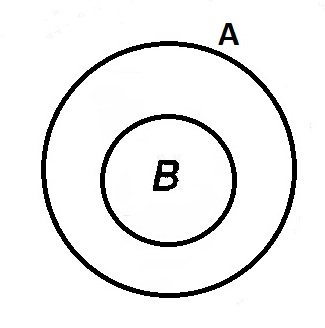 Определение 1.5.Пересечением или произведением множеств A иB называется множество, состоящее из элементов, каждый из которых принадлежит множеству A и множествуBодновременно. Пересечение множеств обозначают A 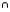 B (илиA·B). Кратко можно записать: B (илиA·B). Кратко можно записать:A 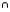 B = B =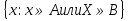 . .A 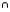 B =A ·B B =A ·BЕслиB 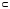 A, тоA · B= B A, тоA · B= B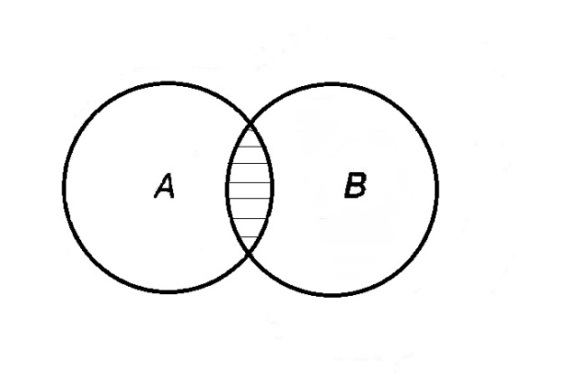 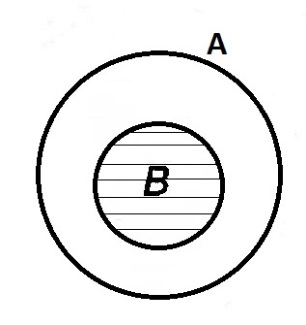 Определение 1.6. Разностью множеств A иB называется множество, каждый элемент которого является элементом множества Aи не является элементом множестваB. Разность множеств обозначают A/B. По определению A/B = 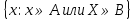 . .A/B =A–B 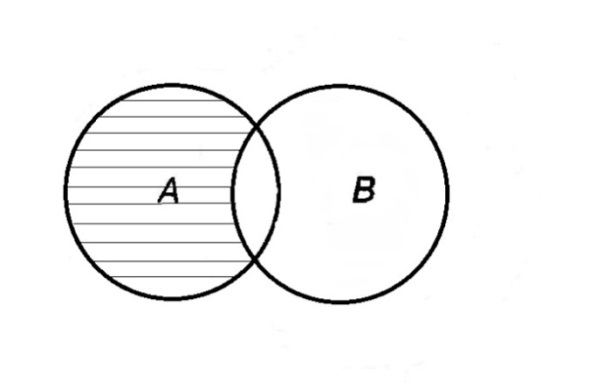 Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются: N = 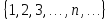 - множество натуральных чисел. - множество натуральных чисел.Z= 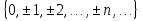 - множество целых чисел. - множество целых чисел.Q= 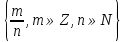 - множество рациональных чисел. - множество рациональных чисел.R‒ множество действительных чисел. Множество Rсодержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, 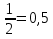 ; ; 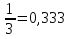 … ‒ рациональные числа. … ‒ рациональные числа.Иррациональное число выражается бесконечной непериодической десятичной дробью. Так, 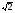 = 1,41421356...; = 1,41421356...; 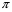 = 3,14159265.... – иррациональное число. = 3,14159265.... – иррациональное число.K– множество комплексных чисел (вида Z=a+bi) R 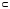 K KОпределение 1.7.Ɛ ‒ окрестностью точки x0 называется симметричный интервал (x0 – Ɛ; x0 + Ɛ), содержащий точку x0. В частности, если интервал (x0 –Ɛ; x0 +Ɛ), то выполнятся неравенство x0 –Ɛ<x<x0 +Ɛ, или, что то же, │x– x0 │<Ɛ. Выполнение последнего означает попадание точки xв Ɛ – окрестность точки x0. Пример 1: 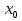 = 2, Ɛ = 0,1. = 2, Ɛ = 0,1.(2 – 0,1; 2 + 0,1) или (1,9; 2,1) – Ɛ– окрестность. 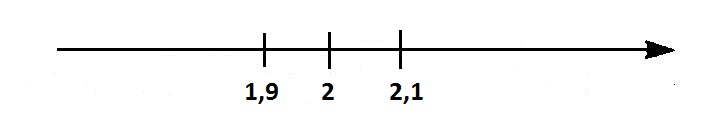 │x– 2│< 0,1 –0,1<x – 2<0,1 2 –0,1<x< 2 + 0,1 1,9<x< 2,1 Пример 2: A– множество делителей 24; B– множество делителей 18. A= 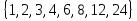 . .B= 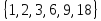 . .A  B= A +B = B= A +B = 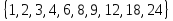 A 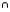 B =A ·B = B =A ·B = 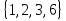 A /B =A –B = 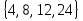 |
