лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Лекция 2. ФУНКЦИЯПонятие функции. Основные свойства функции.Определение 1. Пусть даны два непустых множестваХ и Y.Соответствие f, при котором каждому элементу x  Хсоответствует один единственный элемент у Хсоответствует один единственный элемент у Y, называется функцией и записывается у = f(x), Y, называется функцией и записывается у = f(x), x  Хили f:x→ у (x → у). Хили f:x→ у (x → у).x— аргумент функции; у — значение функции. Пример: y = 2 x – 1 X0 – 1 2 3 – 1Y –3 3 5 Множество Хназывается областью определения функцииfи обозначается D(f). Множество всех у  Yназывается множеством значений функцииfи обозначается E(f). Yназывается множеством значений функцииfи обозначается E(f).Если элементами множеств Х и Yявляются действительные числа, то функцию fназывают числовой функцией. Основные элементарные функции и их графики.Определение 2. Основными элементарными функциями принято называть степенную, показательную, логарифмическую, тригонометрические и обратные тригонометрические функции. Ниже приведены графики этих функций, которые наглядно характеризуют их основные свойства. 1) Показательная функция y = αx, a>0, a 1; 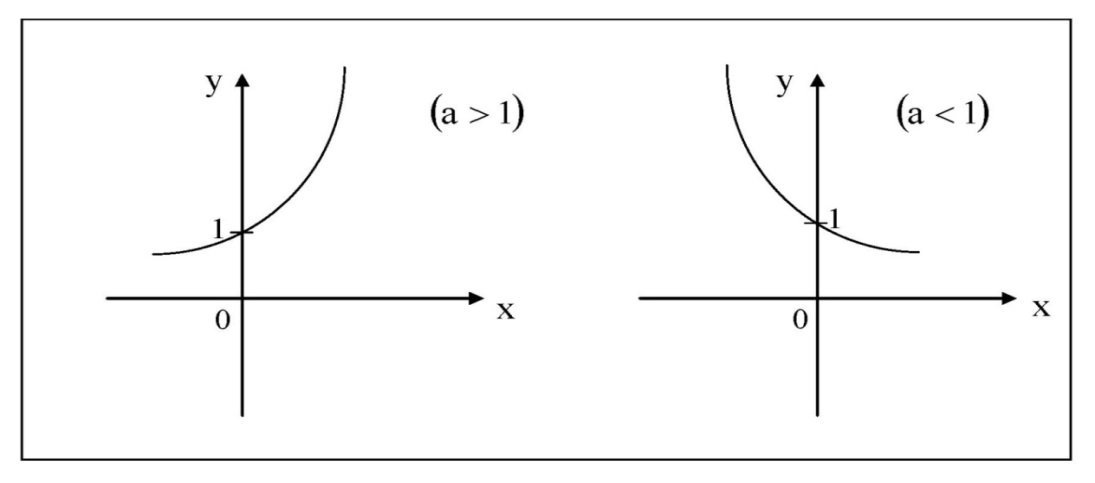 Рис. 1 2) Степенная функция y = x α , α ∈ R . Графики степенных функций, соответствующих различным показателям степени, представлены на рис. 2 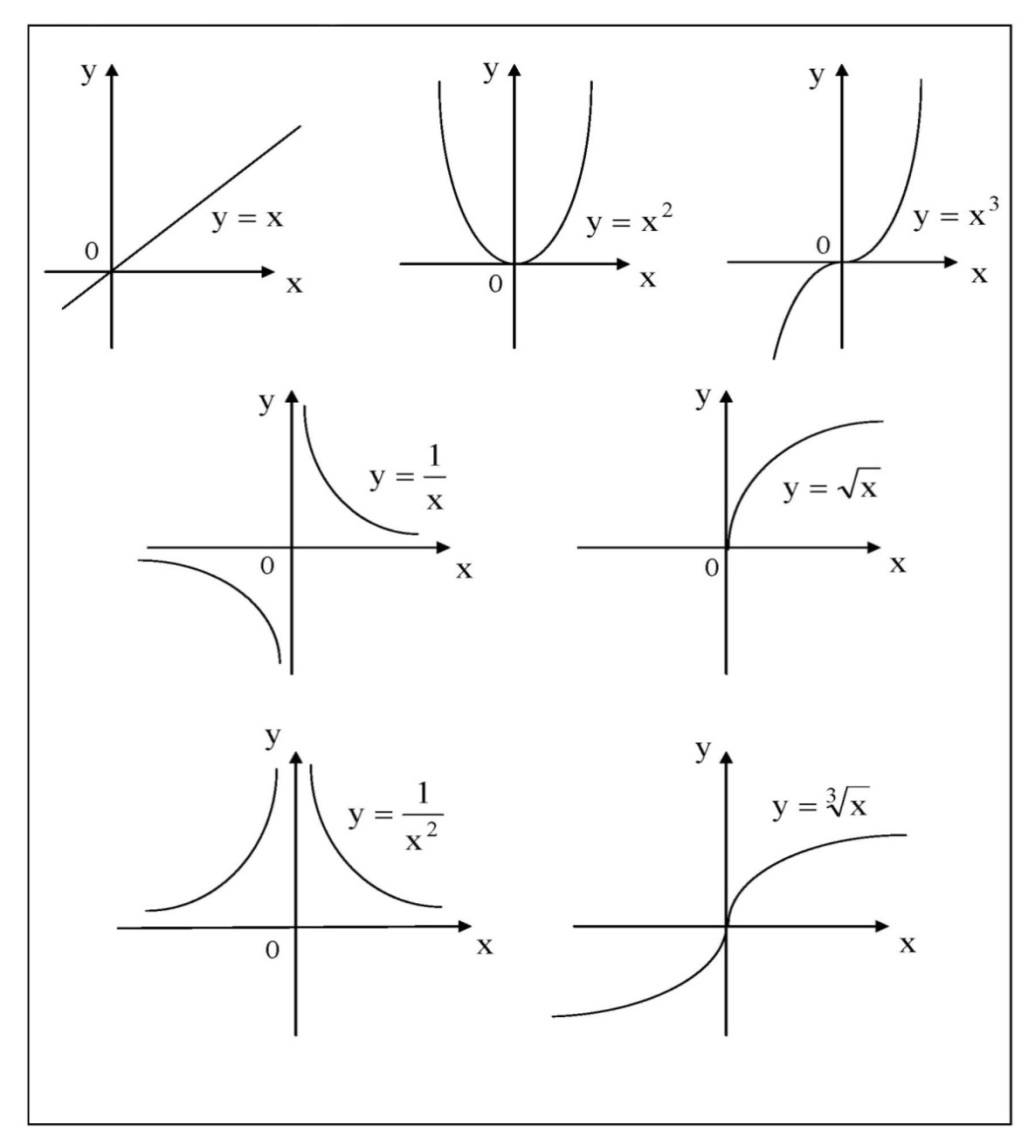 Рис. 2 3) Логарифмическая функция y = logax, a> 0, a 1; 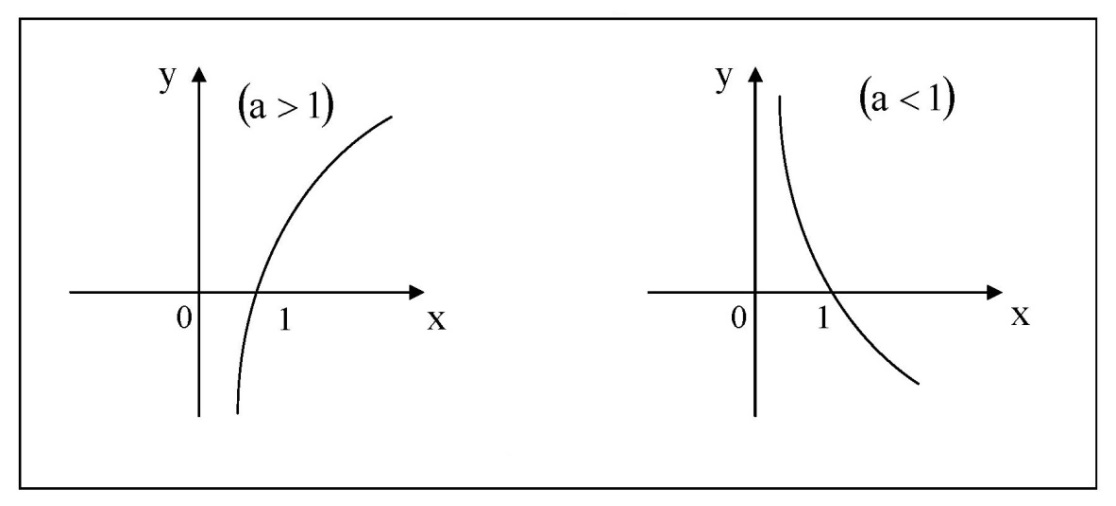 Рис. 3 4) Тригонометрические функцииy = sinx, y = cosx, 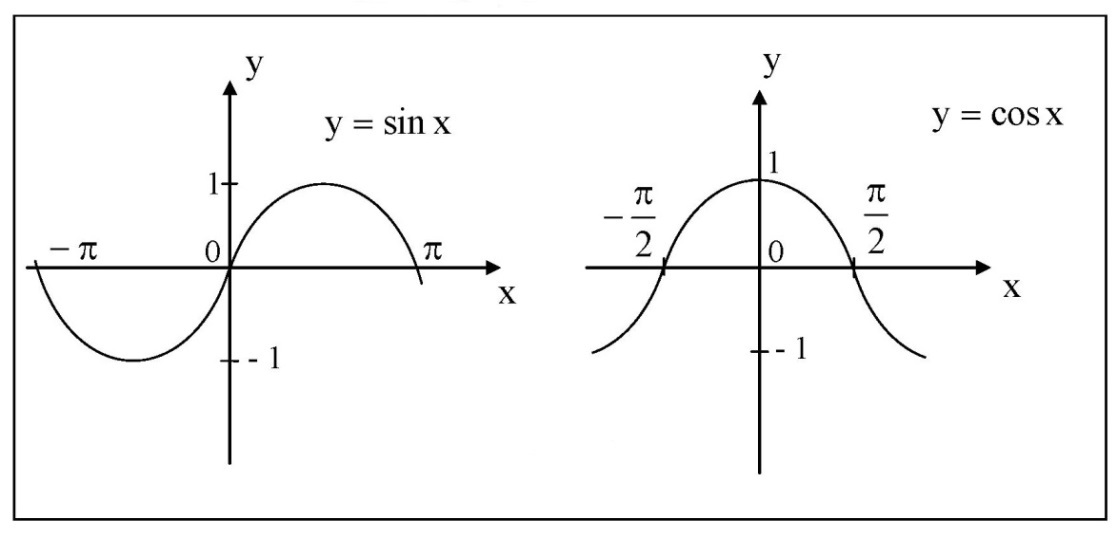 Рис. 4 y = tgx, y = ctgx 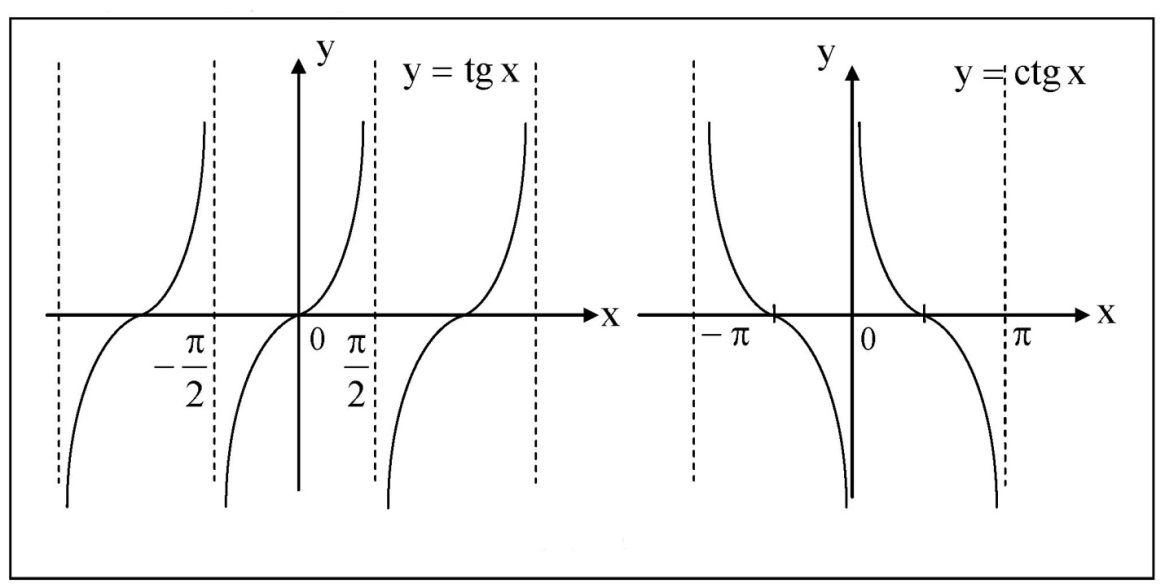 Рис. 5 5) Обратные тригонометрические функции y = arcsinx, D (f) = [-1; 1], E (f) = 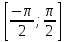 ; ;y = arccos x, D (f ) = [- 1; l], E (f) = 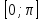 ; ;y = arctg x, D (f) = R, E (f) = 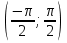 ; ;y = arcctg x, D (f) = R, E (f) = 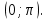 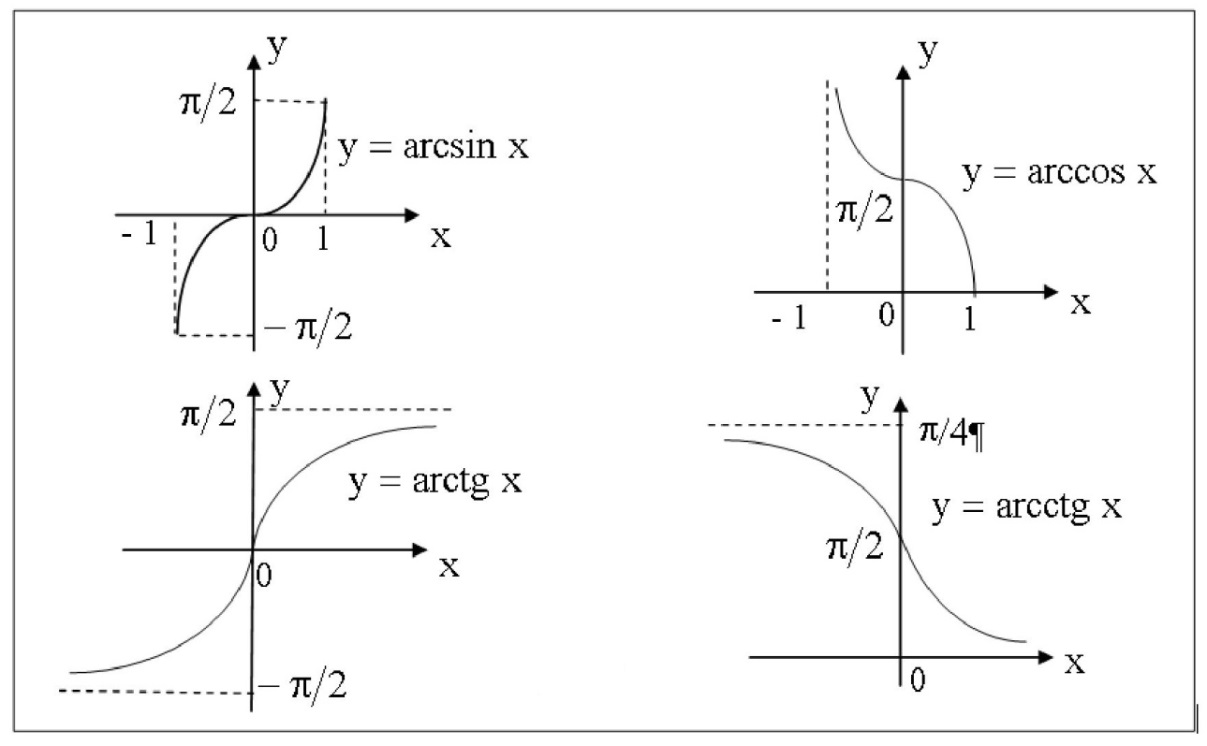 Рис. 6 Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных величин с помощью конечного числа арифметических операций сложения, вычитания, умножения, деления и операций взятия функции от функции, называется элементарной функцией. Примерами элементарных функций являются: у = ax + b–линейная функция a,b∈ R; у = ax + bx + c– квадратичная функция a, b, с ∈ R; у = 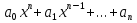 – целая рациональная функция или многочлен степениn, – целая рациональная функция или многочлен степениn,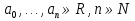 ; ;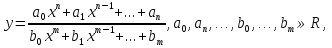 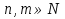 – дробно‒рациональная функция; частным случаем дробно‒рациональной функции является дробно‒линейная функция – дробно‒рациональная функция; частным случаем дробно‒рациональной функции является дробно‒линейная функция 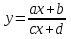 , , 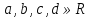 . .Примерами неэлементарных функций могут служить у =sinx = 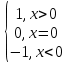 , у = , у =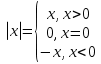 |
