лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Примеры применения производной в экономике.Рассмотрим примеры применения производной в экономике. Задача 1. Зависимость между издержками производства 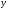 и объемом выпускаемой продукции и объемом выпускаемой продукции 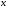 выражается функцией выражается функцией 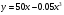 (ден.ед.) Определить средние и предельные издержки при объеме продукции 10 единиц. (ден.ед.) Определить средние и предельные издержки при объеме продукции 10 единиц.Решение: Средние издержки (на единицу продукции) выражаются отношением: 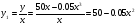 , при , при 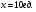 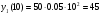 (д.е.) – средние издержки. (д.е.) – средние издержки.Предельные издержки выражаются функцией 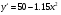 при 10 ед. получим при 10 ед. получим 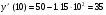 (д.е) – предельные издержки. (д.е) – предельные издержки.Таким образом, средние издержки на производство единицы продукции составляют 45ден.ед., но предельные издержки (т.е. дополнительные затраты на производство дополнительной единицы продукции при данном уровне производства) составляют 35ден.ед. Задача 2. Зависимость между себестоимостью единицы продукции 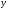 (тыс.руб.) и выпуском продукции (тыс.руб.) и выпуском продукции 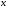 (млрд.руб.) выражается функцией: (млрд.руб.) выражается функцией: 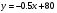 . Найти эластичность себестоимости при выпуске продукции, равном 60 млрд.руб. . Найти эластичность себестоимости при выпуске продукции, равном 60 млрд.руб.Решение: По формуле 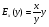 , , 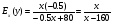 При 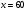 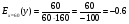 То есть при выпуске продукции, равном 60 млрд.руб., увеличение выпуска на1% приводит к снижению себестоимости на 0.6%. Задача 3. Опытным путем установлены функции спроса 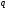 и предложения и предложения 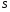 . . 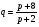 , , 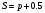 , , где 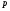 ‒ цена товара, ‒ цена товара, 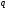 ‒ количество покупаемого товара; ‒ количество покупаемого товара; 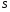 ‒ количество товара, предлагаемого на продажу в единицу времени. ‒ количество товара, предлагаемого на продажу в единицу времени.Найти: а) равновесную цену (т.е. цену, когда спрос равен предложению); б) эластичность спроса и предложения для этой цены; в) изменение спроса при увеличении цены на 5% от равновесной. Решение: а) равновесная цена определяется из условия: 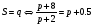 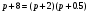 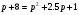 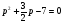 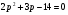 ; ; 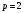 ‒ равновесная цена. ‒ равновесная цена.б) эластичность по спросу и предложению 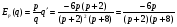 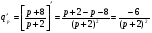 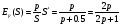 Для равновесной цены 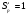 ; ; 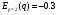 ; ; 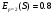 Так как 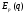 , , 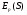 по абсолютной величине <1, то и спрос, и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это значит, что изменение цены не приведет к резкому изменению спроса и предложения. Т.е. при увеличении цены по абсолютной величине <1, то и спрос, и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это значит, что изменение цены не приведет к резкому изменению спроса и предложения. Т.е. при увеличении цены 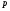 на 1% спрос уменьшится на 0,3%, а предложение увеличится на 0,8%. на 1% спрос уменьшится на 0,3%, а предложение увеличится на 0,8%.в) При увеличении цены p на 5% от равновесной спрос уменьшится на 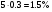 , а, следовательно, доход возрастает на 5%‒1,5%=3,5%. , а, следовательно, доход возрастает на 5%‒1,5%=3,5%.Лекция 7. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ.Исследование функции на монотонность (возрастание и убывание функции)Теорема. Для того чтобы, дифференцируемая в интервале (a, b), функция y = f (x) возрастала (убывала) на интервале (a, b)необходимо и достаточно, чтобы ее производная f ′(x) ≥ 0 (f ′(x) ≤ 0)для∀ x ∈ (a,b). 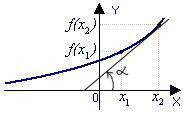 Рис. 1 График возрастающей функции f ′(x) = kкас = tgα> 0, т. к. α – острый угол. 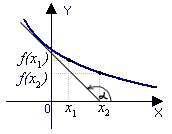 Рис. 2 График убывающей функции tgα< 0, т. к. α – тупой угол. |
