лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Лекция 3.ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИЧисловые последовательности. Пределчисловойпоследовательности.Пусть каждому натуральному числу nпоставлено в соответствие действительное число xп. Тогда говорят, что задана последовательность чисел x1, x2, x3, …, xn, … . Числа x1, x2, x3, …, xn, будем называть элементами (или членами)последовательности, xn–общимчленомпоследовательности. Сокращенно последовательность обозначается 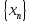 . .Например: 1) 1, 3, 5, …, 2n – 1 – арифметическая прогрессия. d = 2;xn= 2n – 1; x100 = 2 ·100 – 1 = 199. d =x2 – x1 = x3– x2 = … – разность прогрессии. 2) 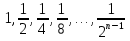 – геометрическая прогрессия. – геометрическая прогрессия.q= 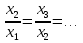 – знаменатель прогрессии. – знаменатель прогрессии.x5= 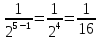 ; ;3) 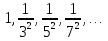 xn= 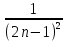 ; ;Определение 1. Последова тельность {xn} называется ограниченной, если она ограничена и сверху и снизу, то есть существуют числа mиMтакие, что любой элемент этой последовательности удовлетворяет неравенствам: 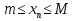 Пример: 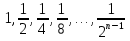 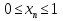 В противном случаи последова тельность {xn} называется неограниченной. Пример: 1, 2, 3, …, n – неограниченная последовательность. Определение 2. Числоa называется пределом числовой последовательности {xn}, если для любого сколь угодно малого ε> 0найдетсячисло N (номер), зависящее от ε, такое, что для всех натуральных чисел n>Nвыполняется неравенство: 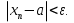 Тогда последовательность {xn} называется сходя щейся,и в этом случае пишут: 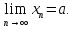 Пример: 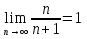 Для любого 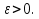 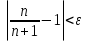 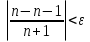 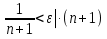 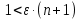 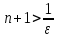 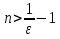 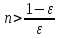 Так как 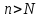 , то , то 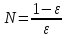 Пусть 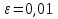 , тогда , тогда 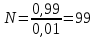 . .Следовательно 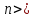 99. 99.Например: 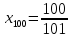 , тогда , тогда 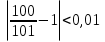 . .Лекция 4.ПРЕДЕЛ ФУНКЦИИПредел функции в точке и в бесконечности. Основные теоремы о пределах.Бесконечно малые и бесконечно большие функции.Пусть функция y =f(x) определена в некоторойокрестностиx0,кроме, может быть, самой точки x0. Определение. ЧислоA называется пределом функцииy =f(x) в точке x0 (или при х →x0), если для любого сколь угодно малого числа ε> 0найдетсятакоечисло δ> 0, что для всех х x0, удовлетворяющих неравенству │ х –x0│< δ, выполняется неравенство│f(x) –А│<ε. Или кратко: 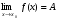 Геометрический смысл предела функции заключается в следующем: число 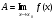 , если для любой ε – окрестности точкиAнайдется такая δ – окрестность точки x0, что для всех х x0 из этой окрестности соответствующие значения функции f(x) лежат в ε – окрестности точки А. , если для любой ε – окрестности точкиAнайдется такая δ – окрестность точки x0, что для всех х x0 из этой окрестности соответствующие значения функции f(x) лежат в ε – окрестности точки А. 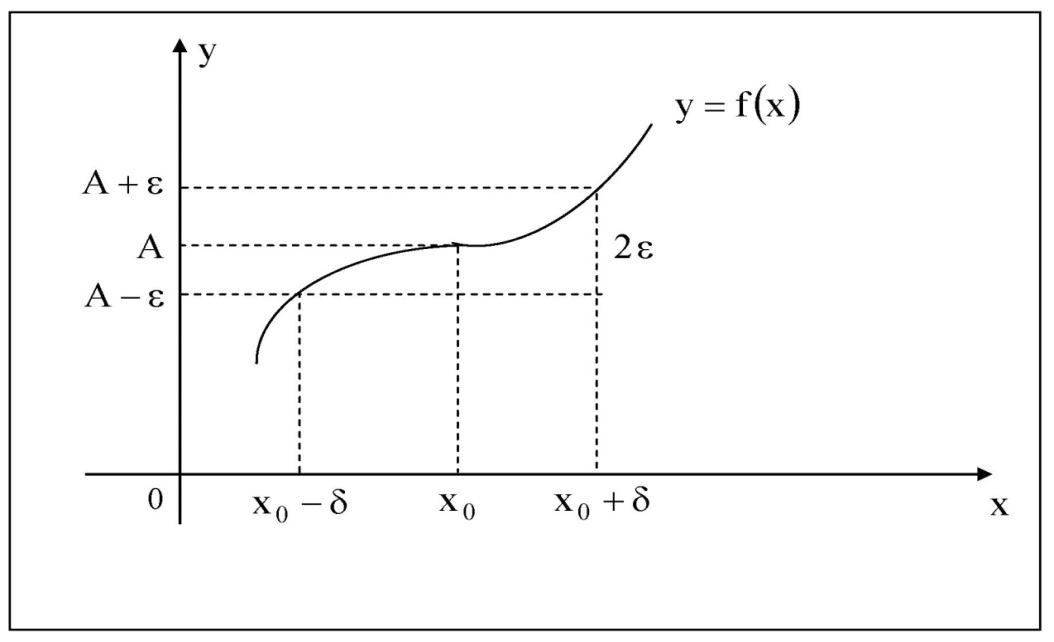 Рис. 1 Пример:Доказать, что 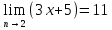 Решение. Возьмем произвольное 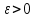 и найдем и найдем 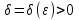 такое, что для всех x, удовлетворяющих неравенству, такое, что для всех x, удовлетворяющих неравенству, 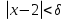 , выполняется неравенство , выполняется неравенство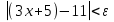 , то есть , то есть 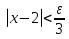 . . Взяв 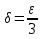 , видим, что для всех x, удовлетворяющих неравенству, , видим, что для всех x, удовлетворяющих неравенству, 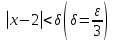 , выполняется неравенство , выполняется неравенство 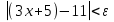 , следовательно, , следовательно,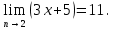 Пусть функция y =f(x) определена в промежутке (–  ; + ; + ). ). Определение. ЧислоA называется пределом функцииf(x) при х 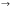  , если для любого числа ε > 0существуеттакоечисло M = M (ε) > 0, что для всех значений x, удовлетворяющих неравенству │x│>M,выполняется неравенство │f(x) – А│< ε. В этом случае пишут , если для любого числа ε > 0существуеттакоечисло M = M (ε) > 0, что для всех значений x, удовлетворяющих неравенству │x│>M,выполняется неравенство │f(x) – А│< ε. В этом случае пишут 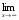 f(x) = А. f(x) = А.Или кратко: 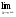 f(x) = А. f(x) = А.Бесконечно малые и бесконечно большие функции. Определение 1. Функция f(x) называется бесконечно большойфункцией при х →x0, если 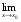 f(x) = f(x) = 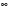 . .Определение 2. Функцияf(x) называется бесконечно малой функцией при х →x0, если 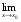 f(x) = 0. f(x) = 0.Основные теоремы о пределах функций. Теорема 1. Предел постоянной величины равен самой постоянной: 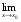 c = c. c = c.Теорема 2. Пределсуммы (разности) двух функций равен сумме (разности) их пределов: 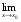 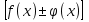 = = 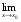 f(x) f(x)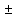 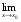 φ(x). φ(x).Теорема 3.Пределпроизведения двух функций равен произведению их пределов: 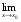 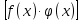 = = 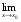 f(x) f(x) 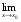 φ(x). φ(x).Теорема 4. Предел дроби равен пределу числителя, деленному на передел знаменателя, если предел знаменателя не равен нулю: 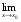 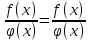 , , 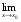 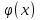 0. 0.Теорема 5. (О пределе промежуточной функции) Если в окрестности точки x0выполняются неравенства: 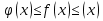 и и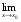 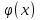 = = 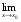 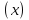 = А, то = А, то 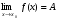 . . |
