лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Лекция 6. ПРОИЗВОДНАЯ ФУНКЦИИ.МЕХАНИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.Производная функции называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю. Производная функции в общем виде: Производная функции в точке x0: Операция нахождения производной называется дифференцированием. Пример 1. y = C; где С = const ∆y = C – C = 0; 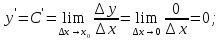 Пример2. 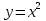 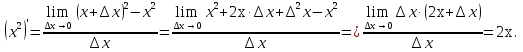 Производная степенной функции: 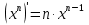 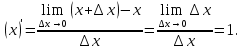 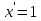 Механический смысл производной связан с производной от пути. Производная от пути в некоторый момент времени равняется скорости в этот момент времени. Sʹ (t0) = U (t0)или Sʹt = U Sʹʹ (t0) = Uʹ (t0) = a (t0) Пример 3. 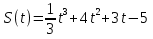 , ,t0 = 1c, Решение: 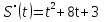 U (t0 = 1) = 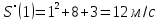 Sʹʹ (t) = 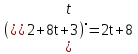 a (t0 = 1) = Sʹʹ (1) = 2 · 1 + 8 = 10 м/с2 Вывод: Производная – это скорость изменения функции. Геометрический смысл производной. 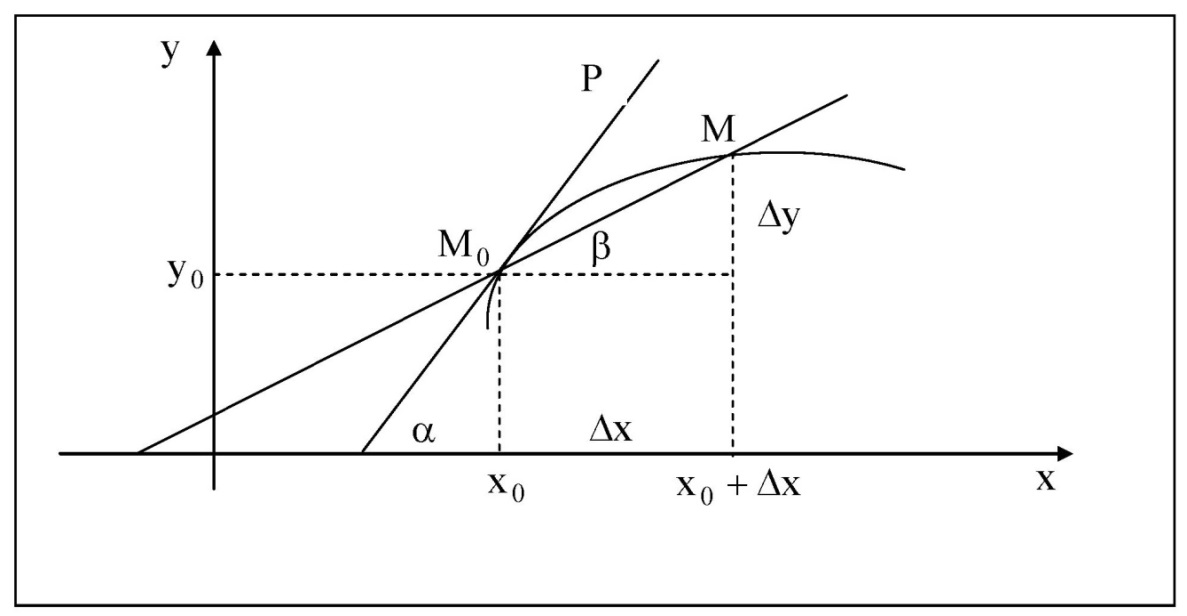 Рис. 1 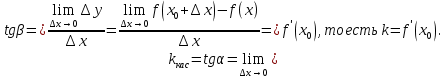 Значение производной функции y = f (x)в точке 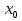 равно угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна равно угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна 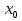 . .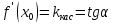 Воспользовавшись уравнением прямой 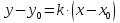 , получим уравнение касательной: , получим уравнение касательной: 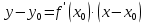 Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой. Из условия перпендикулярности двух прямых 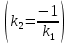 , получим уравнение нормали. Так как , получим уравнение нормали. Так как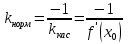 Тогда уравнение нормали имеет вид: 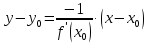 Пример 4. Найти уравнение нормали и касательной к параболе. 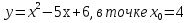 Решение: 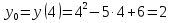 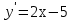 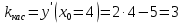 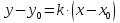 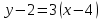 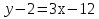 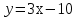 – уравнение касательной. – уравнение касательной.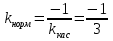 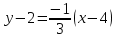 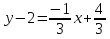 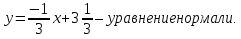 Теорема. Пусть функции 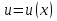 и и 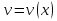 – дифференцируемы в точке x. Тогда: – дифференцируемы в точке x. Тогда:1) Производная суммы (разности) двух функций: 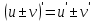 2) Производная произведения двух функций: 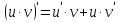 3) Производная частного двух функций: 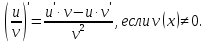 4) Производная от переменной равна единице: 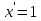 5) Производная сложной функции Пусть 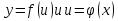 , тогда , тогда 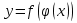 является сложной функцией переменной x, а переменную и называют промежуточным аргументом. является сложной функцией переменной x, а переменную и называют промежуточным аргументом.Сложная функция– это зависимость двух и более функций друг от друга. Производная сложной функции находится по формуле: 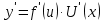 и и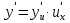 Пример_2_.___Пример_3'>Пример 5. 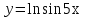 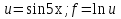 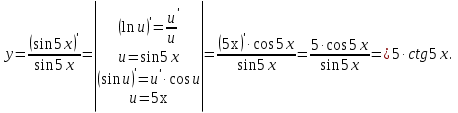 6) Производная обратной функции Пусть функция 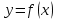 строго монотонна в интервале строго монотонна в интервале 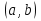 , тогда для нее существует обратная функция , тогда для нее существует обратная функция 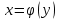 . .Находится по формуле: 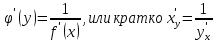 Пример 6. 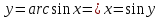 Так как 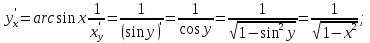 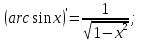 Аналогично выводятся производные других функций. 7) Производные гиперболических функций. Гиперболические функции определяются следующими формулами: 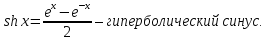 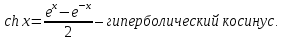 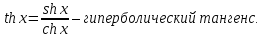 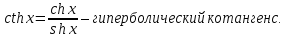 Производные гиперболические функции находятся по формулам: 1. 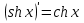 2. 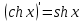 3. 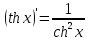 4. 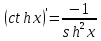 Техника дифференцирования: Пример 1. 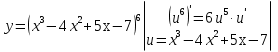 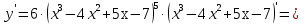 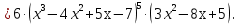 Пример2. 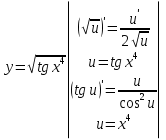 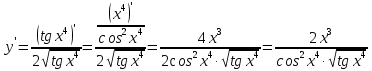 Пример3. 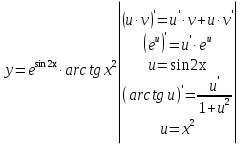 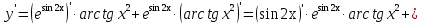 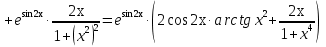 Пример4. 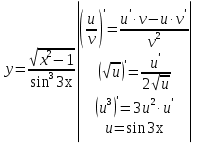 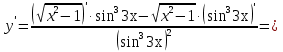 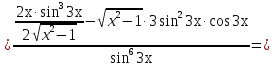 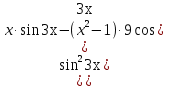 |
