лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Исследование функции на выпуклость и точку перегиба.Функция y = f (x) называется выпуклойвверх на промежутке (a, b), если ее график лежит под касательной, проведенной в любой точке этого промежутка, и называется выпуклой вниз (вогнутой), если ее график лежит над касательной. Точка, при переходе через которую выпуклость сменяется вогнутостью или наоборот, называется точкой перегиба. Алгоритм исследования на выпуклость и точку перегиба: 1. Найдем 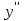 и критические точки второго рода, то есть точки в которых вторая производная равна нулю или не существует. и критические точки второго рода, то есть точки в которых вторая производная равна нулю или не существует.2. Нанести критические точки на числовую прямую, разбивая ее на промежутки. Найти знак второй производной на каждом промежутке; если 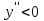 , то функция выпуклая вверх, если , то функция выпуклая вверх, если 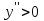 , то функция выпуклая вниз. , то функция выпуклая вниз.3. Если при переходе через критическую точку второго рода 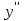 поменяет знак и в этой точке вторая производная равна нулю, то эта точка ‒ абсцисса точки перегиба. Найти ее ординату поменяет знак и в этой точке вторая производная равна нулю, то эта точка ‒ абсцисса точки перегиба. Найти ее ординату 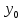 . .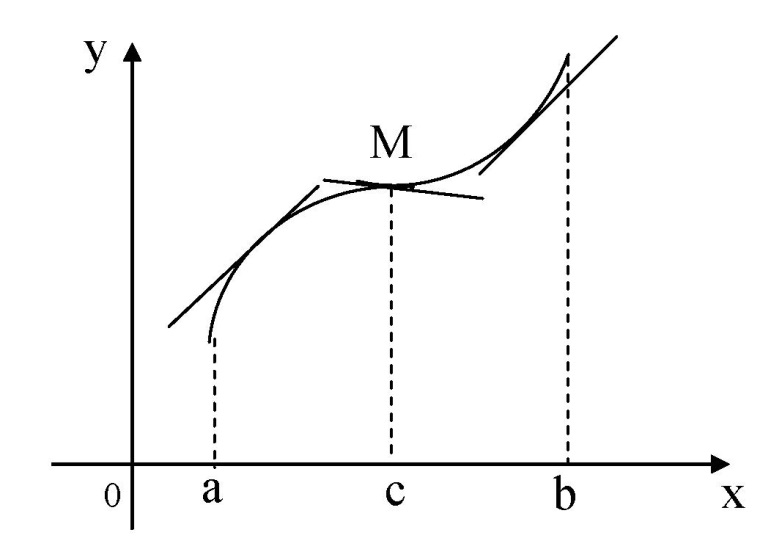 Рис.5 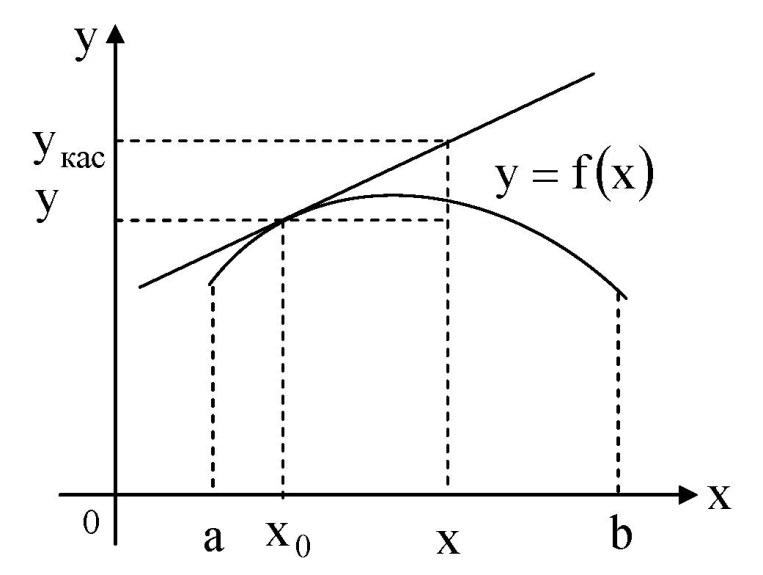 Рис. 6 Асимптоты графика функции. Исследование функции на асимптоты.Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от любой точки графика до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. 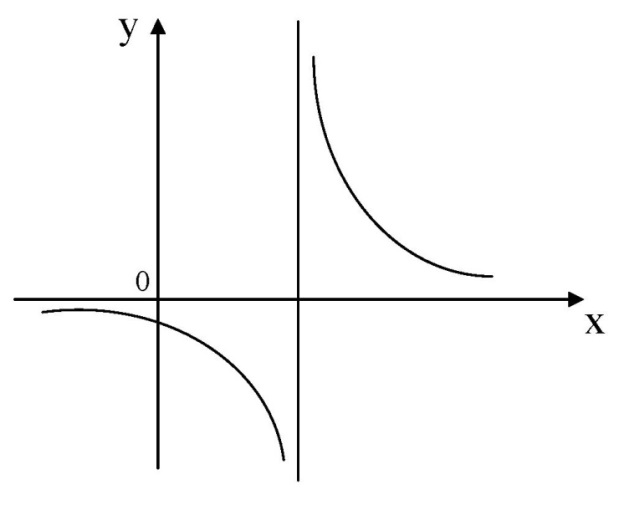 Рис. 7 Существуют три вида асимптот: вертикальные, горизонтальные и наклонные. Определение. Прямая 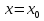 называется вертикальной асимптотойграфика функции у = f (х), если хотя бы один из односторонних пределов функции в этой точке равен бесконечности, то есть называется вертикальной асимптотойграфика функции у = f (х), если хотя бы один из односторонних пределов функции в этой точке равен бесконечности, то есть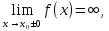 где 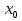 ‒ точка разрыва функции, то есть ‒ точка разрыва функции, то есть 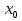 не принадлежит области определения. не принадлежит области определения.Пример. 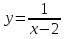 D (y) = (‒ ∞; 2) 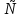 (2; + ∞) (2; + ∞)x= 2 ‒ точка разрыва. 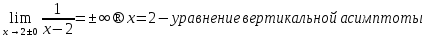 Определение.Прямая у = A называется горизонтальной асимптотой графика функции у = f(х) при 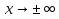 , если , если 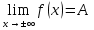 Пример. 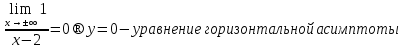
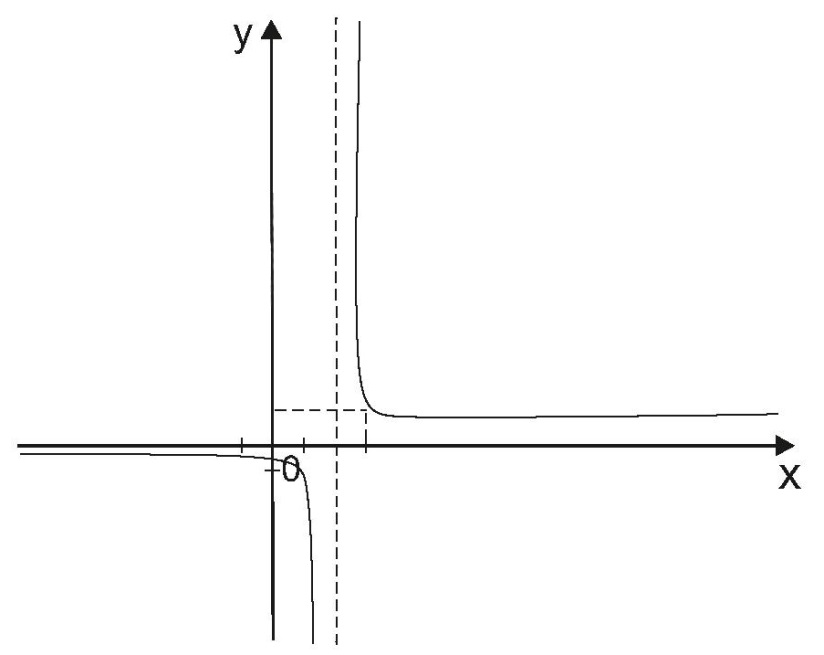 Определение. Прямая у = kх + b (k≠ 0) называется наклонной асимптотой графика функции у = f (х) при 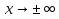 , где , где 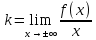 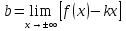 |