лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Экстремум функции (исследование функции на экстремум)Определение. Точка x0называется точкой максимума (минимума) функции y = f (x), если существует δ − окрестность точки x0, такая, что для всех x ≠ x0 из этой окрестности выполняется неравенствоf (x)< f (x0), (f (x)< f (x0)). Определение.Значение функции в точках максимума (минимума) называют экстремумами функции (extmax, extmin). 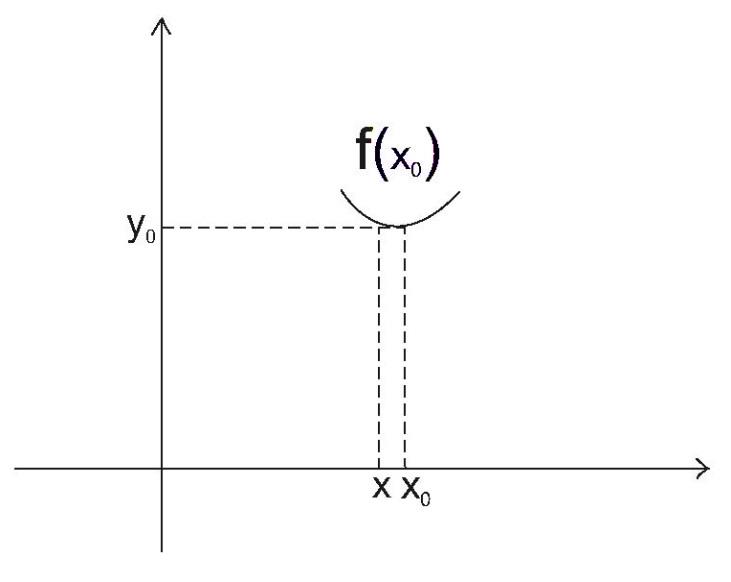 Рис. 3 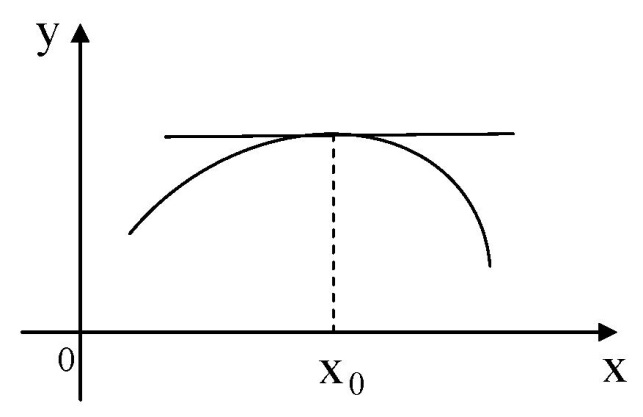 Рис. 4 Теорема (необходимое условие экстремума). Если дифференцируемая функция у = f(х) в точке 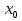 имеет экстремум, то ее производная в этой точке равна нулю, то есть имеет экстремум, то ее производная в этой точке равна нулю, то есть 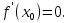 Теорема (достаточное условие экстремума). Если функция у = f (х) дифференцируема в некоторой окрестности критической точки 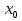 (кроме, быть может, самой точки (кроме, быть может, самой точки 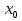 ) и при переходе аргументаx через нее слева направо производная ) и при переходе аргументаx через нее слева направо производная 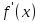 меняет знак с плюса на минус, то меняет знак с плюса на минус, то 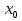 ‒ точка максимума; если ‒ точка максимума; если 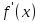 меняет знак с минуса на плюс, то меняет знак с минуса на плюс, то 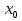 ‒ точка минимума. ‒ точка минимума.Определение. Точки, в которых производная 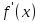 равна нулю или не существует, называются критическими точками функции. равна нулю или не существует, называются критическими точками функции.Пример.Исследовать функцию на монотонность и экстремумы. 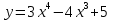 Решение: 1) D (y) = R, то есть 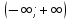 . .2) 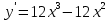 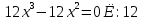 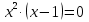 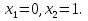 Эти критические точки разбивают всю область определения функции на интервалы: (˗∞; 0), (0; 1) и (1; +∞). Полученные результаты удобно представить в виде следующей таблицы: Эти критические точки разбивают всю область определения функции на интервалы: (˗∞; 0), (0; 1) и (1; +∞). Полученные результаты удобно представить в виде следующей таблицы:
Из таблицы видно, что в точке х = 0 нет экстремума, а х = 1 ‒ точка минимума. Минимум этой функции равен: 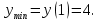 Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на знаке второй производной. 3) y(0) = 5, (0; 5) ˗ точка пересечения с OY. Наибольшее и наименьшее значение функции на отрезке.Пусть функция у = f (х) непрерывна на отрезке [a, b]. Как известно, такая функция на этом отрезке достигает наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке отрезка [a, b], либо на границе отрезка. Для нахождения наибольшего и наименьшего значений функции на отрезке [a, b] необходимо: 1)найти критические точки функции в интервале (a, b); 2)вычислить значения функции в найденных критических точках; 3) вычислить значения функции на концах отрезка, то есть при x= а и х = b; 4)из всех вычисленных значений функции выбрать наибольшее и наименьшее. Пример. Найти наибольшее и наименьшее значения функции 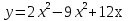 на отрезке [0; 3]. на отрезке [0; 3].Находим критические точки: 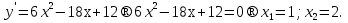 Эти точки лежат внутри отрезка [0; 3]; y(1) = ‒ 3; y(2) = ‒ 4; y(0) = ‒ 8; y(3) = 1; Эти точки лежат внутри отрезка [0; 3]; y(1) = ‒ 3; y(2) = ‒ 4; y(0) = ‒ 8; y(3) = 1;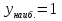 в точке x = 3 и в точке x = 3 и 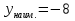 в точке x = 0. в точке x = 0. |