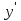лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
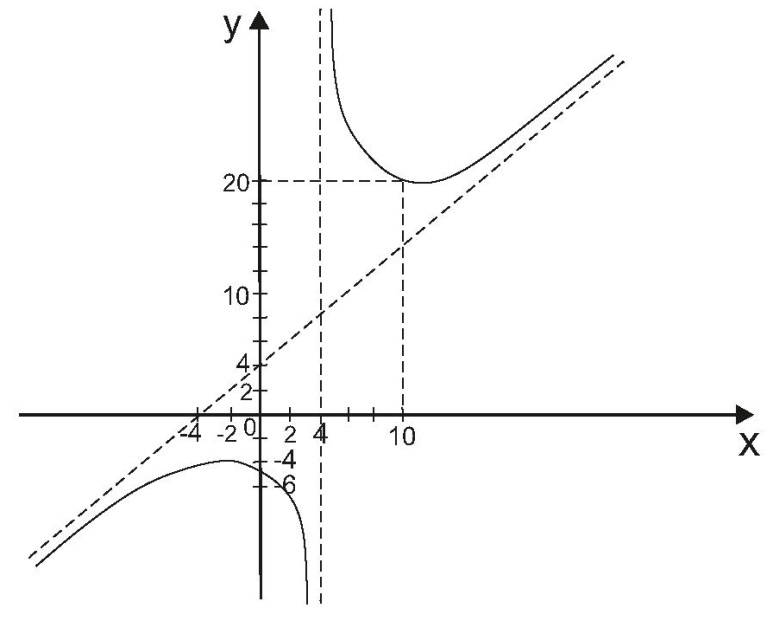
Общая схема исследования функций и построения графиков.Алгоритм исследования функции у = f (х): 1. Найти область определения функцииD (y). 2. Найти (если это можно) точки пересечения графика с осями координат (при x = 0 и при y = 0). 3. Исследовать на четность и нечетность функции(y (‒x) = y (x) ‒четность; y(‒x) = ‒y (x) ‒нечетность). 4. Найти асимптоты графика функции. 5. Найти интервалы монотонности функции. 6. Найти экстремумы функции. 7. Найти интервалы выпуклости (вогнутости) и точки перегиба графика функции. 8. На основании проведенных исследований построить график функции. Пример. Исследовать функцию и построить ее график. 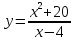 1) D (y) = 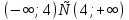 x = 4 ‒ точка разрыва. 2) При x = 0, 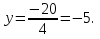 (0; ‒ 5) ‒ точка пересечения с oy. При y = 0, 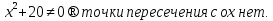 3) y(‒ x)= 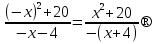 функция общего вида (ни четная, ни нечетная). функция общего вида (ни четная, ни нечетная).4) Исследуем на асимптоты. а) вертикальные 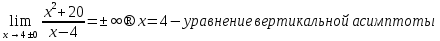 б) горизонтальные 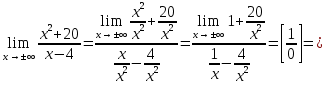 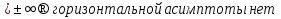 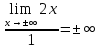 в) найдем наклонные асимптоты 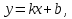 где где 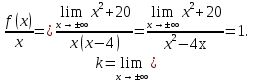 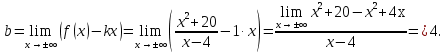 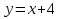 ‒ уравнение наклонной асимптоты ‒ уравнение наклонной асимптоты5) В данном уравнении не требуется найти интервалы монотонности функции. 6)  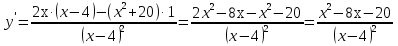 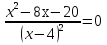 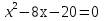 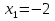 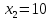 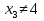 Эти критические точки разбивают всю область определения функции на интервале (˗∞; ˗2), (˗2; 4), (4; 10)и (10; +∞). Полученные результаты удобно представить в виде следующей таблицы:
Из таблицы видно, что точках = ‒2‒точка максимума, в точкех = 4‒нет экстремума, х = 10 ‒точка минимума. Подставим значение (‒ 3) в уравнение: 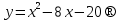 9 + 24 ‒ 20 > 0 9 + 24 ‒ 20 > 00 ‒ 20 < 0 25 ‒ 40 ‒ 20 < 0 121 ‒ 88 ‒ 20 > 0 Максимум этой функции равен 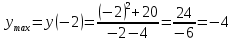 (‒ 2; ‒ 4) ‒ экстремум максимальный. Минимум этой функции равен 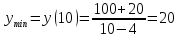 (10; 20) ‒ экстремум минимальный. 7) исследуем на выпуклость и точку перегиба графика функции 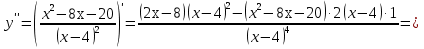 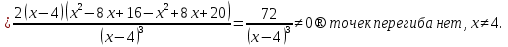 8) 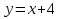
 |