лекции по математическому анализу. кубанский государственный аграрный университет мультимедийные лекции
 Скачать 12.08 Mb. Скачать 12.08 Mb.
|
Лекция 14.ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯПЕРВОГО ПОРЯДКА.Это дифференциальные уравнения вида: 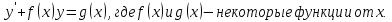 Решается подстановкой: 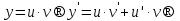 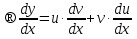 Подставим полученное в уравнение 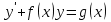 : :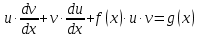 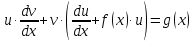 Подставив в равенство 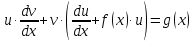 значение функции u, получим дифференциальное уравнениес разделяющимся переменными.Решив которое, найдем функцию v, а затем и функцию y. значение функции u, получим дифференциальное уравнениес разделяющимся переменными.Решив которое, найдем функцию v, а затем и функцию y.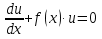 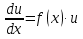 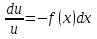 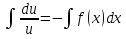 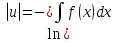 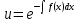 Пример. 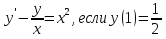 Решение: 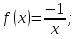 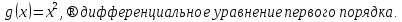 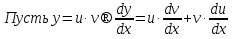 Подставим в уравнение 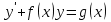 , ,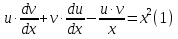 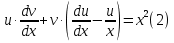 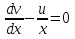 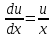 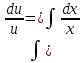 Подставим значения uв равенство (2), получим: 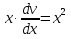 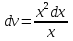 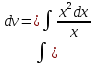 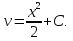 Тогда, 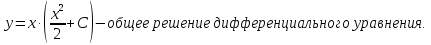 Так как при x=1, 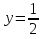 , то подставив в общее решение, получим: , то подставив в общее решение, получим: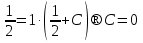 Подставим значение Cв общее решение, получим: 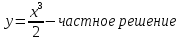 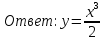 Проверка: 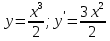 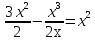 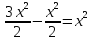 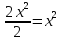 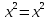 Лекция 15.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА.Иногда решение дифференциальных уравнений второго порядка можно свести к последовательному решению двух дифференциальных уравненийпервого порядка. Тогда говорят, что дифференциальное уравнение допускает понижение порядка. Это дифференциальные уравнения вида: 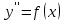 или 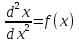 Пример 1. 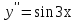 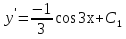 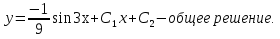 Пример 2. 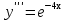 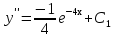 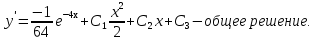 Уравнения этого типа решаются заменой переменной 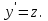 Следовательно, Следовательно,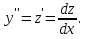 Подставим в дифференциальное уравнение 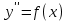 . .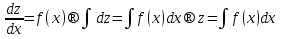 Подставив значение zв дифференциальное уравнение 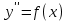 , найдем функцию y. , найдем функцию y. Пример. 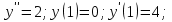 Решение: 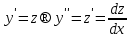 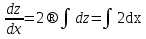 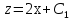 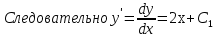 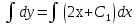 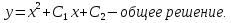 Так как при x= 1, y = 0 и при x = 1, 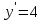 , то , то 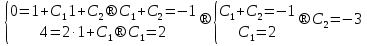 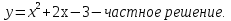 Ответ:  . . |
