|
|
Курс лекций НЭ_ч4-ч5_Богач_2013. Курс лекций " Основы наноэлектроники"
В твердых растворах пересыщенных определенным компонентом, при последующей термообработке возможно образование множества зародышей, которые в дальнейшем превращаются в более равновесные включения новой фазы. Процесс зародышеобразования как правило протекает равномерно по объему (или по поверхности) твердого тела. Такие процессы оказываются проще технологий на основе литографий. Спонтанная кристаллизация широко используется для создания структур с квантовыми точками без использования литографических методов. Этим методом формируют нанокристаллиты в неорганических и органических материалах.
4.5.1.Самосборка в объемных материалах.
Движущей силой самоорганизующихся процессов является стремление атомной системы принять конфигурацию, соответствующую минимуму ее потенциальной энергии. Из таких процессов в твердых телах наиболее значимым и часто используемым является процесс спонтанной кристаллизации. Кристаллическое состояние вещества является более устойчивым, чем аморфное. Поэтому любая аморфная фаза предрасположена к кристаллизации. Закономерности этого процесса определяются как индивидуальными физикохимическими свойствами самой среды, в которой он протекает, так и внешними условиями, в которых эта среда находится. Главной характеристикой среды является температура.
Образование кристаллических зародышей понижает энергию системы на Δg= gam - gcr , где кристаллическая фаза характеризуется энергией gcr , а аморфная энергией gam . Этому снижению энергии противостоит увеличение поверхностной энергии растущих зародышей. Для Δg , рассчитываемого на единицу объема новой фазы, появление зародышей с радиусом r и удельной поверхностной энергией σ* приводит к общему изменению свободной энергии системы на величину
ΔG = 4∙π∙r2∙σ* - (4/3)∙π∙r3∙Δg. (4.1)
Изменение свободной энергии происходит с ростом размера (радиуса) зародыша немонотонно, как это показано на рис. 4.2.
Образование поверхности зародышей требует совершения работы над системой, в то время как формирование кристаллического объема зародышей освобождает энергию в системе. Изменение свободной энергии имеет максимум для кластера с критическим радиусом
rcr = 2∙ σ*/Δg. (4.2)
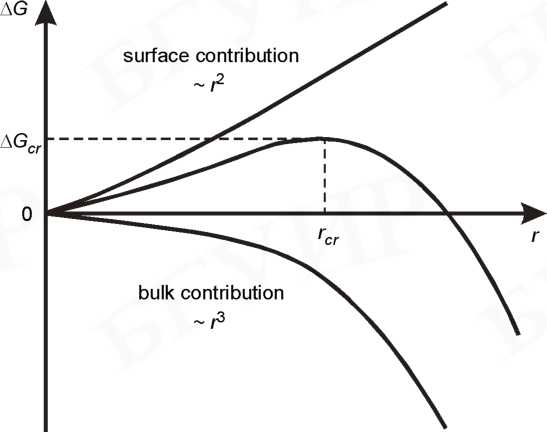
Рис. 4.2. Изменение свободной энергии кристаллического зародыша в зависимости от его радиуса.
Образование кластеров с радиусом меньше критического требует положительного изменения свободной энергии, и система в таких условиях оказывается нестабильной. При этом существует некоторое динамически равновесное количество таких кластеров. Кластеры с размером больше критического имеют благоприятные энергетические условия для роста. Скорость зарождения кристаллитов vn пропорциональна концентрации зародышей с критическим размером и скорости, с которой эти зародыши образуются:
vn exp(-ΔGcr /kBT)∙exp(-Ea/kBT), (4.3)
где ΔGcr - свободная энергия образования критического зародыша, kB - постоянная Больцмана, Т - абсолютная температура. Член exp(-Ea/kBT) представляет вклад диффузии атомов в зарождение и последующий рост зародышей. Он характеризуется энергией активации Еа. Поскольку ΔGcrобратно пропорционально T2, скорость зародышеобразования изменяется как ехр(-1/T3). Очевидно, что зарождение каждой определенной фазы происходит в узком температурном интервале, ниже которого ничего не происходит, а выше реакции протекают чрезвычайно быстро.
Примеры двуокись кремния в кремнии.
4.5.2.Самосборка при эпитаксии.
При осаждении одного материала на подложку из другого материала возможно три варианта формирования поверхностных структур. Они показаны на рис. 4.3.
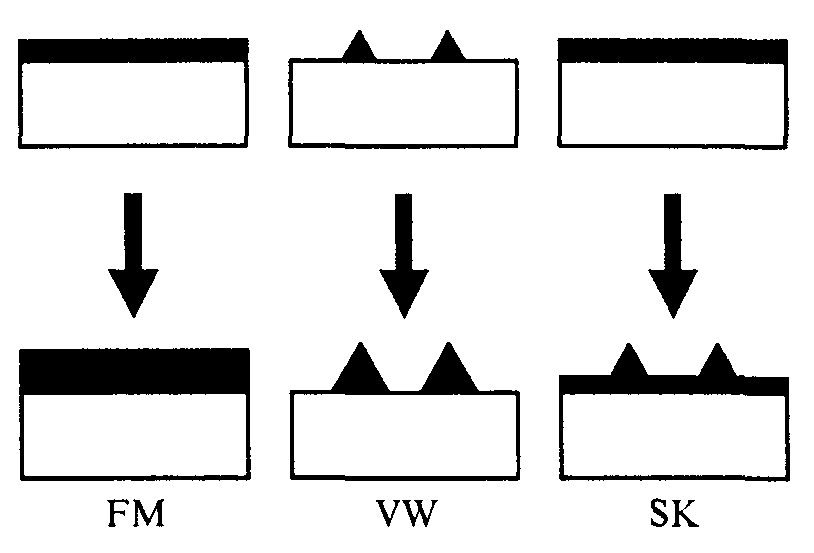
Рис. 4.3. Режимы роста тонких пленок. Схематическое изображение трех режимов роста для гетероэпитаксиальных систем: Франка—ван дер Мерве (FM), Фолмера—Вебера (VW) и Странского—Крастанова (SK).
Это послойный рост сплошной пленки (двухмерный рост) в режиме, называемом модой Франка-Ван-дер-Мерве, образование и рост островков (трехмерный рост) - мода Волмера-Вебера, и комбинированный режим - мода Странского-Крастанова, когда изначально пленка растет послойно, а затем трансформируется в островковую структуру. Режим (мода) формирования поверхностных структур определяется рассогласованием параметров решеток подложки и наносимого материала, а также соотношением поверхностной энергии и энергии границы раздела этих материалов.
Важно отметить, что все энергетические аргументы справедливы для равновесного состояния системы. Формирование же эпитаксиальных пленок происходит в условиях, отличающихся от равновесных, что затрудняет их анализ и интерпретацию по энергетическим критериям. Кинетические эффекты, контролируемые температурой подложки и скоростью осаждения материала, существенно влияют на режим формирования поверхностных структур. Тем не менее, энергетические соображения, рассматриваемые ниже, полезны для многих практических случаев, поскольку, по крайней мере, предсказывают поведение различных систем в равновесных и квазиравновесных условиях.
В системе, образованной материалами с согласованными параметрами решеток, режим роста определяется только соотношением поверхностной энергии и энергии границы раздела. Если сумма поверхностной энергии эпитаксиальной пленки и энергии границы раздела меньше, чем поверхностная энергия подложки, (осаждаемый материал смачивает подложку), имеет место послойный рост пленки в режиме Франка-Ван-дер-Мерве. При этом формируются однородные когерентные псевдоморфные и напряженные сверхрешетки. Этот режим пригоден также для создания самоорганизующихся квантовых шнуров на вицинальных поверхностях кристаллов. Вицинальными называют поверхности, которые не являются равновесными для данного кристалла (теорема Вульфа). Обычно это поверхности, слегка разориентированные относительно низкоиндексных плоскостей кристалла - на практике чаще всего используют разориентацию относительно (001) и (311) плоскостей. Рис. 4.4 иллюстрирует основные этапы формирования методом самосборки встроенных квантовых шнуров с использованием вицинальной поверхности кристалла.
Рис. 4.4. Создание квантовых шнуров самосборкой в процессе эпитаксиального роста на вицинальной поверхности: а - подготовленная вицинальная поверхность; б - нанесение материала шнура; в - нанесение половины монослоя материала шнура; г - добавление материала подложки до полного монослоя; д - встроенный квантовый шнур, созданный повторением в и г.
Подготовленная вицинальная поверхность состоит из равнодистанционно расположенных террас, плоскость которых совпадает с одной из низкоиндексных плоскостей кристалла. Высота каждой террасы соответствует одному моноатомному слою. Создание квантовых шнуров начинают с нанесения материала, из которого будет формироваться шнур. Температуру подложки выбирают таким образом, чтобы обеспечить достаточную диффузионную подвижность атомов наносимого материала на поверхности подложки. Осажденным атомам энергетически более выгодно прикрепляться к ступеньке террасы, нежели находиться на ее поверхности. Количество наносимого материала составляет лишь долю от той величины, которая необходима для покрытия подложки сплошным моноатомным слоем. Это необходимо для того, чтобы оставить место на террасе для заполнения материалом подложки, что и делается после прекращения подачи материала шнура. Нанесение материала подложки продолжают до полного восстановления террас, которые при этом становятся на один моноатомный слой толще. Нанесение материала шнура, а затем подложки повторяют несколько раз, обеспечивая, таким образом, создание квантового шнура, встроенного в подложку. Основной проблемой в практической реализации представленного подхода является волнообразный характер границ террас, что приводит к таким же волнообразным шнурам. Чтобы получить строго линейные шнуры, поверхность искусственно профилируют канавками, вдоль которых и происходит самоорганизованный рост (сборка) квантовых шнуров.
Однородные напряженные эпитаксиальные пленки начинают расти послойно, даже когда имеется рассогласование решеток наносимого материала и подложки. Накопление энергии в напряженном состоянии по мере увеличения толщины пленки неизбежно ведет к образованию островков, что понижает общую энергию в системе. Такие превращения происходят при эпитаксии в режиме Странского-Крастанова. При этом образуются самособирающиеся нанокристаллические эпитакисальные островки на монокристаллической подложке. Переход от двухмерного послойного роста сплошной пленки к трехмерному росту островков (2D →3D переход) имеет место, когда межатомные расстояния в кристаллической решетке осаждаемого материала больше, чем в решетке подложки. Островковая структура энергетически более благоприятна для релаксации напряжений, нежели слоистая. Релаксация напряжений в двухмерном слое может осуществляться только в направлении, перпендикулярном плоскости этого слоя. В островке напряжения имеют возможность релаксировать как в самом островке, так и вокруг него.
Рассмотрим поведение общей энергии системы, образуемой рассогласованными кристаллическими решетками, в зависимости от продолжительности нанесения материала, полагая, что скорость нанесения материала мала для проявления динамических эффектов. Изменение общей энергии для этого случая схематически показано на рис. 4.5. Материал, подвергающийся сжатию на подложке, наносится с постоянной скоростью вплоть до момента времени, обозначенного X. Различимы три основных периода, обозначенных А, В и С.
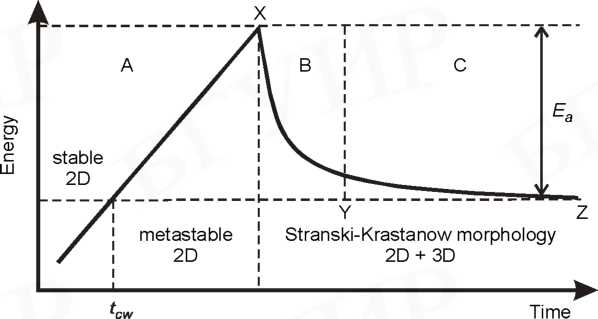
Рис. 4.5. Изменение во времени полной энергии эпитаксиальной структуры, растущей в режиме Странского-Крастанова.
В начальный период А послойным ростом формируется двухмерная эпитаксиальная пленка. Поверхность подложки идеально смочена наносимым материалом. Упругие напряжения линейно возрастают с увеличением объема нанесенного материала. В момент времени tcw смачивающий слой достигает критической толщины, когда послойный рост становится метастабильным. При дальнейшем поступлении материала создаются суперкритические условия, в которых все еще сплошной эпитаксиальный слой готов к разрыву и переходу в режим роста трехмерных островков по механизму Странского-Крастанова. Временной диапазон существования метастабильного состояния определяется высотой энергетического барьера для этого перехода Еа .
Период В, представляющий 2D →3D переход, т.е. фрагментацию суперкритического смачивающего слоя, начинается, когда накопленной упругой энергии становится достаточно для преодоления энергетического барьера этого перехода в момент времени X. Предполагается, что, уже начавшись, 2D →3D переход может продолжаться без дальнейшего поступления материала, используя материал, запасенный в суперкритическом смачивающем слое. Период В включает две стадии - зарождение островков и их последующий рост. Флуктуации толщины пленки или напряжений по поверхности подложки приводят к зарождению островков в определенных местах. Толщина смачивающего слоя, при которой начинается спонтанное зарождение островков, зависит от рассогласования параметров решеток материалов, а также от наносимого материала и от анизотропии свойств подложки. Например, при эпитаксии германия на монокристаллическом кремнии это происходит, когда толщина германия превышает несколько монослоев. Для контролируемого расположения островков в определенных местах подложки ее подвергают предварительной обработке для создания на ее поверхности неоднородностей, служащих центрами зарождения.
Стадия зарождения определяет поверхностную плотность островков. Образование первого сверхкритического зародыша немедленно приводит к фрагментации всего смачивающего слоя. Предполагаемое распределение напряжений в окрестности островка показано на рис. 4.6.
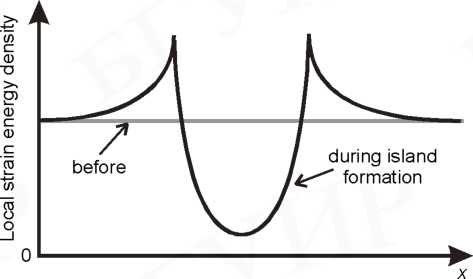
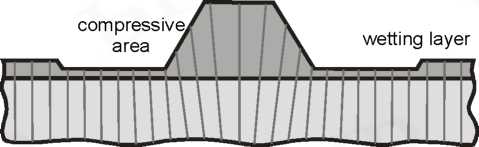
Рис. 4.6. Локальные напряжения на границе с подложкой и деформация решетки в когерентном островке.
Поверхность островка благоприятна для понижения напряжений, максимальная величина которых - у границы с подложкой. Благодаря релаксации напряжений в объеме островка, на поверхности они минимальны. Островок имеет монокристаллическую напряженную бездислокационную структуру.
Последующий рост островков стимулируется избытком материала в суперкритическом смачивающем слое, предшествовавшем фрагментации. Он характеризуется скоростями в десятки раз большими обычных скоростей роста при данной температуре. В процессе роста четко определяются низкоиндексные плоскости {1 1 n} (n = 0, 1,
3), скорость роста на которых ограничена. В результате островки приобретают пирамидальную форму с {113} или {110} гранями или форму усеченных пирамид. Хотя растущие островки когерентны с подложкой, не исключено появление некогерентных островков и дислокаций несоответствия в островках на границе с подложкой, если скорость поступления материала на подложку слишком велика.
Дальнейший рост островков в пределах периода С происходит по механизму дозревания. Система уже растратила большую часть энергии, запасенной в упругих напряжениях. Разность в свободной энергии между большими и маленькими островками приводит к медленному росту больших островков за счет поглощения маленьких. Этот процесс контролируется поверхностной диффузией.
Эпитаксиальное осаждение в режиме Странского-Крастанова успешно используется для создания квантовых точек размером 2-40 нм из полупроводников A3B5, A2B6, SiGe, Ge. Они достаточно однородны по размеру. В них нет дислокаций несоответствия, поскольку благодаря трехмерной релаксации напряжений в окрестностях островка его высота может превышать критическую толщину для псевдоморфного роста. Разработано несколько методов для наномасштабного позиционирования мест зарождения островков, использующих эпитаксиальное осаждение в окна маски, созданной электронно-лучевой или зондовой литографией.
Предложены и безмасочные методы контролируемого создания центров зарождения островков зондом сканирующего туннельного или атомного силового микроскопа. Один из них, используемый для формирования квантовых точек из In As, показан на рис. 4.7.
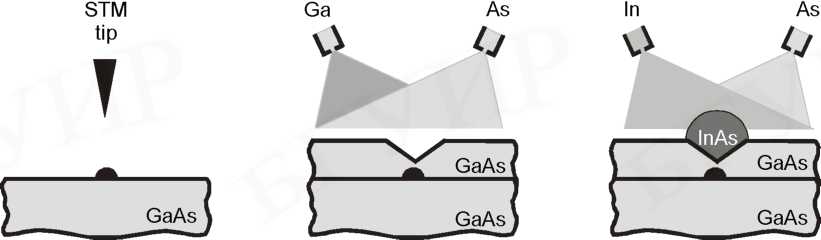
Рис. 4.7. Самосборка квантовых точек из InAs GaAs, отмеченных зондом сканирующего туннельного микроскопа, в процессе эпитаксиального осаждения в режиме Странского-Крастанова.
Процедура начинается с нанесения материала с острия вольфрамового зонда на поверхность GaAs подложки подачей на зонд нескольких импульсов напряжения. Сканируя зонд вдоль поверхности подложки, наноразмерные образования создают в местах желательного расположения квантовых точек.
Нанесенный материал должен быть стабилен в парах мышьяка при температурах до 610 °С, поскольку он действует в качестве наномаски при последующем эпитаксиальном осаждении GaAs. На начальных этапах эпитаксии GaAs сформированные ранее наноостровки остаются непокрытыми, однако при увеличении толщины осажденного GaAs они постепенно закрываются за счет бокового роста над островком. Над островками образуются пирамидальные впадины. Затем проводят эпитаксиальное осаждение InAs. Зарождение и рост самоорганизующихся островков из этого материала происходит исключительно в этих впадинах.
На рис. 4.8 представлено СТМ- изображение сформированной таким образом наноструктуры.

Рис. 4.8. Изображение в сканирующем туннельном микроскопе квантовых точек из InAs на GaAs, созданных самосборкой. Каждая точка имеет высоту 6 нм и диаметр основания 30 нм.
Повторение операций нанесения GaAs и InAs позволяет создавать многослойные структуры с квантовыми точками из InAs, встроенными в GaAs. Причем квантовые точки в них располагаются строго друг над другом в местах, обозначенных предварительным нанесением маскирующего материала с зонда.
Несмотря на то, что детали механизма, контролирующего образование наноразмерных островков, остаются объектом исследования, метод эпитаксиального осаждении материалов в режиме Странского-Крастанова найдет применение для массового производства структур с квантовыми точками, нано- и оптоэлектронных приборов на их основе.
Допматериал.
На рис.2.6 приведены результаты термодинамичского анализа.
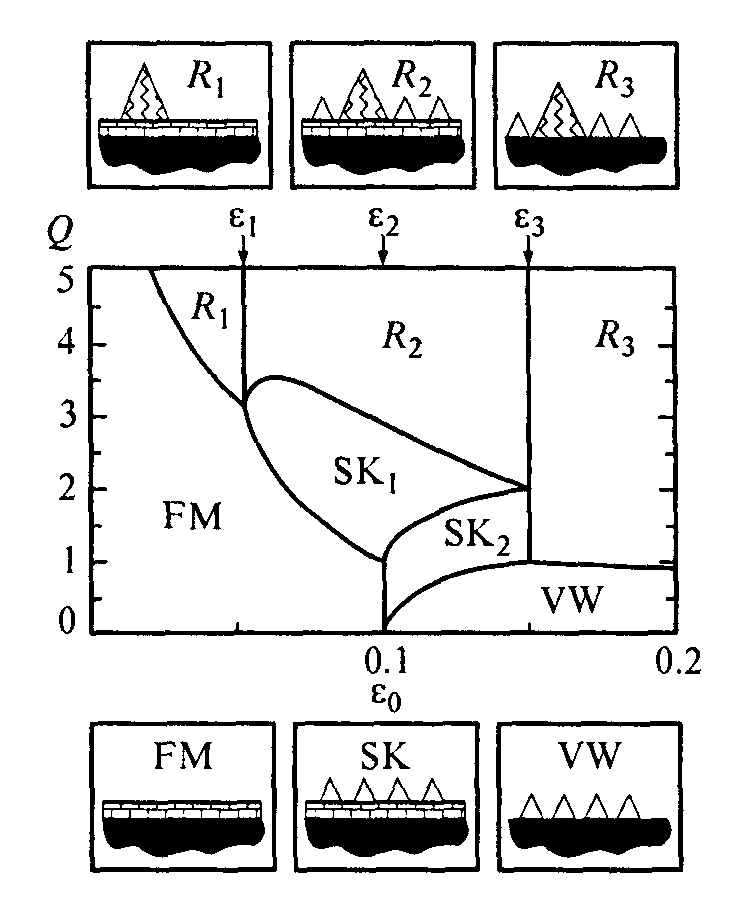
Рис. 2.6. Равновесная фазовая диаграмма гетероэпитаксиальной системы с рассогласованием решеток в осях. Q — количество монослоев осажденного материала; ε0 =Δa/a — рассогласование решеток.
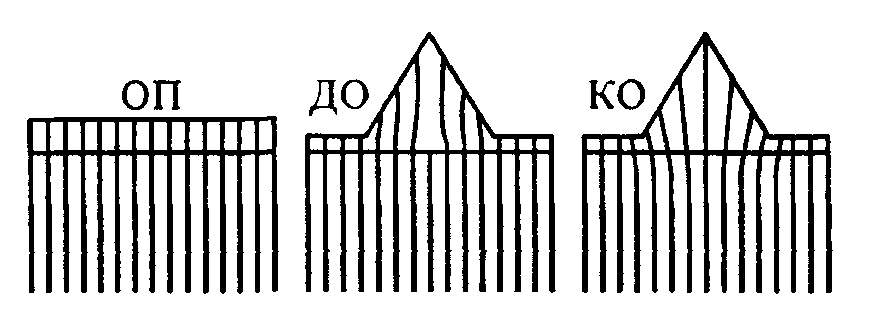
Рис. 2.10. Релаксация упругих напряжений в процессе роста в режиме Странского—Крастанова. Линии обозначают плоскости решетки. ОП — однородная пленка; ДО — дислокационный островок; КО — когерентный
островок.
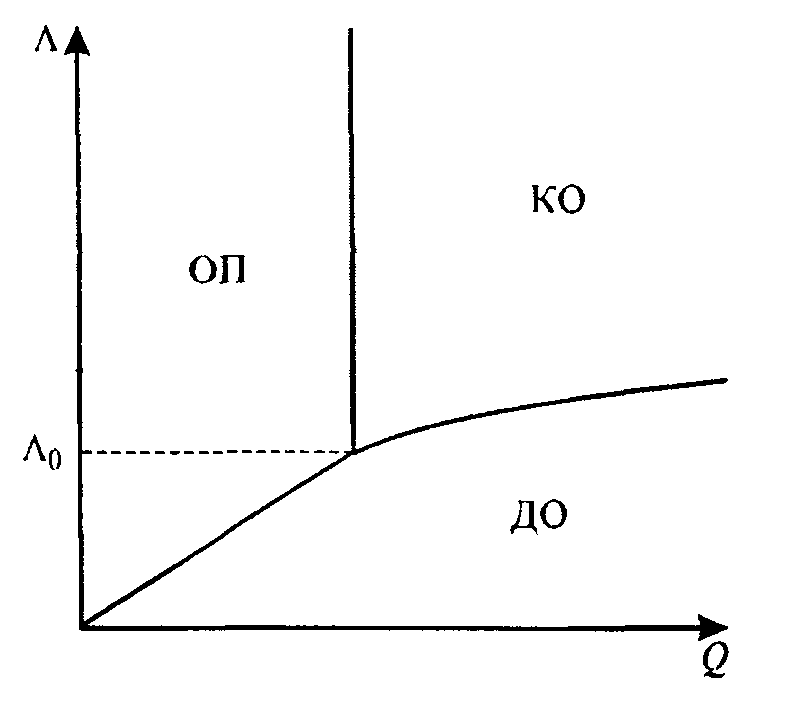
Рис. 2.11. Фазовая диаграмма, показывающая возможные типы структур. Q — количество осажденного материала; Λ — отношение энергий границы раздела с дислокациями и дополнительной поверхностной энергии.
Возможность образования когерентного островка (КО) или островка с дислокациями на границе с подложкой (ДО) определяется отношением энергий боковых поверхностей граней островка ΔЕпов (эта величина всегда положительна) и энергией границы раздела при образовании дислокаций несоответствия Едисл На фазовой диаграмме с осями Λ= Едисл /ΔЕпов и Q — количество монослоев осажденного материала изображены области образования структур разного типа, представленных на рис. 2.10 (рис. 2.11). Как видно из рисунка, если ΔЕпов велика или энергия границы раздела с образованием дислокаций относительно мала, тогда Λ оказывается меньше Λ0 и образование когерентно-напряженного островка невыгодно. В этом случае при увеличении количества осажденного материала происходит переход от однородной напряженной пленки (ОП) к островку с дислокациями на границе и когерентно-напряженные островки не образуются. Если ΔЕпов мала или энергия границы раздела с образованием дислокаций относительно велика, тогда Λ больше Λ0 и при увеличении количества осажденного материала происходит переход от однородной пленки к пленке с когерентными островками. Дальнейшее осаждение материала может привести к образованию дислокаций.
Примеры Шик с 51-53
|
|
|
 Скачать 3.44 Mb.
Скачать 3.44 Mb.









