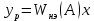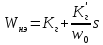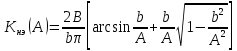Расчёт параметров регулятора. Расчет_параметров_настройки_регуляторов_59. Курсовой проект по дисциплине Теория автоматического управления (наименование дисциплины) А втоматизация технологи на тему Анализ и синтез типовой одноконтурной сар
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
| | (10) |
или
| | (11) |
где
 ,
,Уравнение (11) решаем графически. Для этого необходимо построить на одной комплексной плоскости годограф Найквиста линейной части
SCRIPT 21:
A=2.5:0.01:15;
b=2.4;
B=2.4;
Wnon=((2*B)./(pi*b)).*(asin(b./A)+(b./A).*sqrt(1-b^2./A.^2));
Z=-1./(Wnon);
Re=real(Z);
Im=imag(Z);
b3=1.993; b2=15.71; b1=6.486; b0=0.5069;
a4=120; a3=75.99; a2=30.71; a1=7.486; a0=0.5069;
w=0.05:0.01:3;
W2=( b3*(j*w).^3+b2*(j*w).^2+b1*(j*w)+b0)./(a4*(j*w).^4+a3*(j*w).^3+a2*(j*w).^2+a1*(j*w));
re=real(W2);
im=imag(W2);
 plot(re,im,Re,Im);grid
plot(re,im,Re,Im);gridПостроенные в результате выполнения Script 21 годографы приведены на рисунке 25. Видно, что годографы не пересекаются, значит, автоколебания в системе отсутствуют.
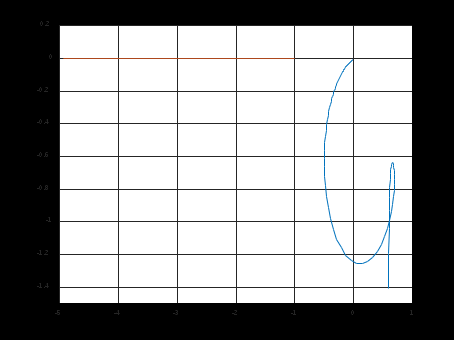
Рисунок 25 – Годографы линеаризованной САР
4.3 Моделирование нелинейной САР в Simulink
Для подтверждения сделанных выводов построим модель САР в Simulink. Схема модели изображена на рисунке 26, переходная характеристика, полученная с помощью этой модели – на рисунке 27.
Блок Transfer Fcn не позволяет задать начальные условия, воспользуемся блоком State Space, для перехода к его использованию напишем скрипт:
SCRIPT 22:
a=[0.9 7 2.2];
b=[120 74 15 1];
[A,B,C,D]=tf2ss(a,b);
Зададим начальное условие y0 = 3:
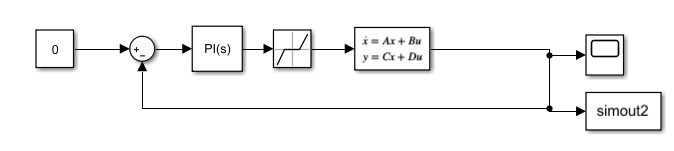
Рисунок 26 – Схема s-модели нелинейной САР
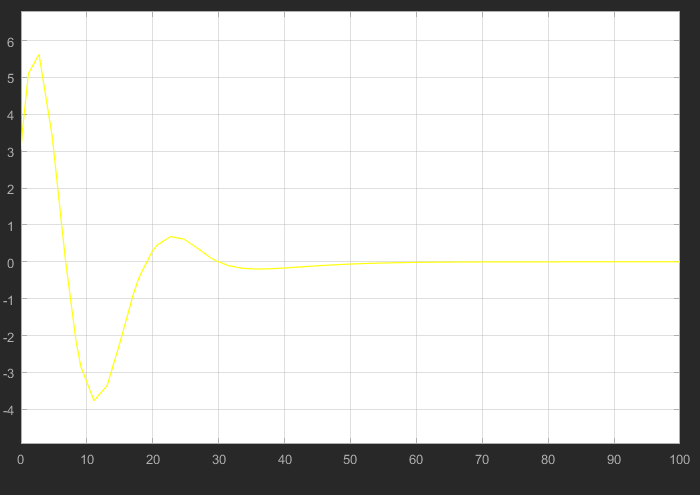
Рисунок 27 – Переходная характеристика нелинейной САР
Автоколебания в системе отсутствуют. Свободная составляющая переходного процесса носит устойчивый характер и с течением времени стремится к 0.

ЗАКЛЮЧЕНИЕ

В ходе выполнения курсового проекта был произведен анализ объекта регулирования, построена кривая разгона ОР.
В результате проведения необходимых расчетов были определены оптимальные параметры настройки П, ПИ, ПИД-регуляторов, запас устойчивости систем, оценено качество переходных процессов САР с П, ПИ, ПИД-регуляторами. Также был проведен анализ наблюдаемости и управляемости САР: система со всеми тремя регуляторами оказалась полностью наблюдаемой и управляемой.
Для случая, когда регулирующий орган имеет нелинейную характеристику был проведен анализ на возможность возникновения автоколебаний в нелинейной системе регулирования методом Гольдфарба. Установлено, что автоколебания в системе невозможны.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
 Линейные и нелинейные системы управления: Методические указания и задания на курсовой проект по курсу «Теория управления» для студентов дневной и заочной форм обучения специальности 2102 – Автоматизация технологических процессов и производств / Составители С. Г. Денисенко, Ю. Е. Кичкарь. Кубан. гос. технол. ун-т; - Краснодар: Изд-во КубГТУ, 2000. – 22 с.
Линейные и нелинейные системы управления: Методические указания и задания на курсовой проект по курсу «Теория управления» для студентов дневной и заочной форм обучения специальности 2102 – Автоматизация технологических процессов и производств / Составители С. Г. Денисенко, Ю. Е. Кичкарь. Кубан. гос. технол. ун-т; - Краснодар: Изд-во КубГТУ, 2000. – 22 с. Теория автоматического управления: Учеб. для вузов по спец. «Автоматика и телемеханика». В 2-х ч. Ч. 1. Теория линейных систем автоматического управления / Н.А. Бабаков, А.А. Воронов, А.А. Воронова и др.; Под ред. А. А. Воронова. ‑ 2-е изд., перераб. и доп. ‑ М.: Высш. шк., 1986. –367 с., ил.

 4
4 
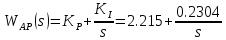

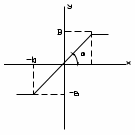
 Для оценки возможности и устойчивости автоколебаний в нелинейной САР по методу Гольдфарба необходимо линеаризовать систему. Применим к нелинейному элементу гармоническую линеаризацию. Тогда передаточная функция звена с насыщением будет иметь вид:
Для оценки возможности и устойчивости автоколебаний в нелинейной САР по методу Гольдфарба необходимо линеаризовать систему. Применим к нелинейному элементу гармоническую линеаризацию. Тогда передаточная функция звена с насыщением будет иметь вид: