Конспект лекций по экологии для заочников. Лекция Краткая история и предмет экологии
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
Смертность. Смертность характеризует гибель особей в популяции. В определенной степени это понятие является антитезой рождаемости. Подобно рождаемости, смертность можно выразить числом особей, погибших за данный период (число смертей за определенный период), или же в виде специфической смертности - по отношению к числу особей, составляющих всю популяцию или ее часть. Экологическая, или реализуемая, смертность - гибель особей в данных условиях среды - величина, которая, подобно экологической рождаемости, не остается постоянной, а изменяется в зависимости от условий среды и состояния самой популяции. Существует некоторая теоретическая минимальная смертность - постоянная величина, характеризующая гибель особей в идеальных условиях, при которых популяция не подвергается лимитирующим воздействиям. Максимальная продолжительность жизни особей в этих оптимальных условиях равна их физиологической продолжительности жизни, которая в среднем обычно намного превышает экологическую продолжительность жизни. Как и в случае рождаемости, нужно знать и минимальную величину смертности (теоретическая константа), и фактическую, или экологическую, смертность (переменная величина); первая служит основой или мерой, которая позволяет производить сравнение. Даже в идеальных условиях в любой популяции происходит гибель особей от "старости", поэтому некоторая минимальная смертность отмечается даже в самых благоприятных условиях, которые можно создать для организма; она будет определяться физиологической продолжительностью жизни особей. Разумеется, поскольку в природе в большинстве популяций средняя продолжительность жизни намного меньше, чем ее потенциальная продолжительность, фактическая величина смертности намного превышает минимальную. Однако в некоторых популяциях или в течение некоторых периодов смертность снижается до величины, которая в практических целях может рассматриваться как минимальная, что дает возможность определять ее в естественных условиях. Смертность, как и рождаемость, особенно у высших организмов, сильно варьирует с возрастом; в связи с этим большой интерес представляет определение специфической смертности для возможно большего числа возрастных групп или стадий развития, поскольку это позволит установить силы, которые лежат в основе механизмов, определяющих общую смертность в популяции. Нередко значительно больший интерес представляет не смертность, а выживание, поэтому целесообразно выражать смертность в виде величины, обратной выживанию. Если число погибших особей составляет М, то выживание равно 1- М. Кривые выживания Целостное представление о смертности в популяциях дают так называемые кривые выживания. Кривую выживания можно получить, если откладывать по оси абсцисс интервалы времени, а по оси ординат - или абсолютное число выживших особей или их процент от исходной популяции: (Число выживших/Численность исходной популяции) * 100% Такие кривые, построенные в относительной или полулогарифмической шкале, причем интервалы времени по оси абсцисс отложены в процентах средней или абсолютной продолжительности жизни, позволяют сравнивать популяции видов, значительно различающихся по длительности жизни. Кривые выживания подразделяются на три общих типа, показанных на рис.16.1. 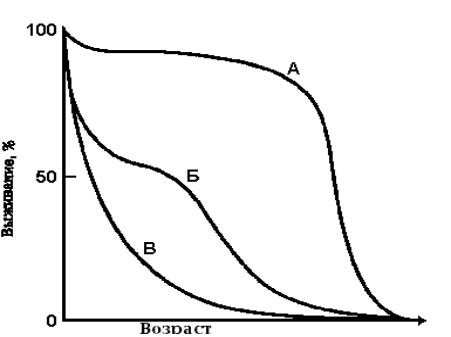 Рис.16.1. Три типа кривых выживания. По оси ординат отложен процент выживших особей от исходной популяции, а по оси абсцисс - возраст в % продолжительности жизни. А - выпуклая кривая (гибель в основном происходит в конце жизни); Б - S-образная, слабо вогнутая кривая (у взрослых особей смертность практически постоянна); В - вогнутая кривая (смертность очень высока на ранних стадиях). Большинство животных и растений подвержено старению, которое проявляется в снижении жизненности с возрастом после периода зрелости. Как только начинается старение, вероятность наступления смерти в определенный промежуток времени возрастает. Непосредственные причины смерти могут быть разными, но в основе их лежит уменьшение сопротивляемости организма к действию неблагоприятных факторов, например болезням. Кривая А на рис. 16.1 очень близка к идеальной кривой выживания для популяции, в которой старение служит главным фактором, влияющим на смертность. Примером может быть популяция человека в современной развитой стране с высоким уровнем медицинского обслуживания и рациональным питанием. Большинство людей доживает до старости, но среднюю ожидаемую продолжительность жизни почти невозможно увеличить более чем до 75 лет. Отклонение кривой от идеальной обусловлено детской смертностью, отображаемой уклоном начального участка. Хотя детская смертность в развитых странах намного ниже, однако, и здесь вероятность смерти в раннем детстве выше средней. Кроме того, на кривую выживания помимо старения влияет фактор случайной гибели, причины которой с возрастом могут изменяться. Наибольшая смертность в результате автомобильных катастроф, например, падает на возраст 20-25 лет. Кривая, сходная с кривой А, свойственна также многим видам крупных животных и однолетним культурным растениям, например пшенице, когда все растения на данном поле стареют одновременно. Прямая противоположность - сильно вогнутая кривая (рис.16.1, В) характерна для популяций организмов с высокой смертностью в ранний период жизни. Такой тип выживания характерен, например, для устриц и других моллюсков и ракообразных, а также для дуба; на стадии свободноплавающей личинки или на стадии прорастания желудя смертность чрезвычайно высока, но как только организм прочно закрепится на благоприятном для него субстрате, ожидаемая продолжительность жизни значительно возрастает. К промежуточному типу относятся кривые выживания тех видов, у которых специфичная для каждой возрастной группы величина выживания остается более или менее постоянной. Слабо вогнутая, или S-образная кривая (рис. 16.1, Б) может быть получена, если смертность постоянна в течение всей жизни организмов (50% за определенную единицу времени). Это может быть тогда, когда главным фактором, определяющим смертность, становится случай, причем особи гибнут до начала заметного старения. Очень сходная кривая характерна для популяций некоторых животных (например, гидры), не подвергающихся особой опасности в раннем возрасте. Для многих птиц, мышей, кроликов, большинства беспозвоночных и растений тоже характерна кривая такого типа, но высокая смертность среди молодых особей приводит к тому, что начальная часть кривой спускается более круто; у взрослых особей (в возрасте 1 год и старше) смертность ниже и более постоянна. "Ступенчатую" кривую выживания можно ожидать в тех случаях, когда на последовательных стадиях жизненного цикла величина выживания существенно различается, как у насекомых, относящихся к группе Holometabola (т.е. у насекомых с полным превращением, например бабочек). Форма кривой выживания связана со степенью родительской заботы или с другими механизмами защиты потомства. Так, кривые выживания для медоносной пчелы и дрозда (которые защищают свое потомство) значительно менее вогнуты, чем кривые для кузнечика и сардины (не защищают потомства). У последних видов отсутствие защиты компенсируется откладкой значительно большего числа яиц. Форма кривой выживания может изменяться в зависимости от плотности популяции. Кривая выживания для более плотной популяции имеет сильно вогнутую форму. Существуют небольшие внутривидовые различия в кривых выживания. Они могут быть обусловлены разными причинами и нередко связаны с полом. У людей, например, женщины живут несколько дольше, чем мужчины, хотя точные причины этого неизвестны. Вычерчивая кривые выживания для различных видов, можно определять смертность для особей разного возраста и таким образом выяснять, в каком возрасте данный вид наиболее уязвим. Установив причины смерти в этом возрасте, можно понять, как регулируется величина популяции. Возрастная структура популяции. Возрастная структура популяции является ее важной характеристикой, которая, оказывает влияние как на рождаемость, так и на смертность. По отношению к популяции можно выделить три экологических возраста: пререпродуктивный, репродуктивный и пострепродуктивный. Длительность этих возрастов относительно продолжительности жизни сильно варьирует у разных организмов и должна быть учтена при интерпретации данных о возрастной структуре. У современного человека эти три "возраста" более или менее одинаковы, на каждый из них приходится примерно треть жизни. Древний человек имел значительно более короткий пострепродуктивный период. Для многих растений и животных характерен очень длительный пререпродуктивный период. У некоторых животных, особенно насекомых, пререпродуктивный период чрезвычайно длителен, репродуктивный период очень короток, а пострепродуктивный период отсутствует. Классические примеры - поденки (Ephemeridae) и семнадцатилетняя саранча. У поденок личиночное развитие в воде занимает от одного до нескольких лет, а во взрослом состоянии они живут всего несколько дней. Саранча обладает чрезвычайно длительным циклом развития (впрочем, необязательно семнадцатилетним), но взрослые насекомые живут менее одного сезона. Соотношение различных возрастных групп в популяций определяет ее способность к размножению в данный момент и показывает, чего можно ожидать в этом отношении в будущем. Обычно в быстро растущих популяциях значительную часть, составляют молодые особи; в стабильных популяциях распределение возрастных групп более равномерно (для того чтобы численность популяции оставалась постоянной, в среднем только два потомка каждой пары должны доживать до репродуктивного возраста); а в популяциях с уменьшающейся численностью больше старых особей. Однако возрастная структура популяции может меняться и без изменения ее численности. Для каждой популяции характерна некоторая "нормальная", или стабильная, возрастная структура, к которой направлено изменение ее реальной возрастной, структуры. Коль скоро достигается стабильная возрастная структура, необычное увеличение рождаемости или смертности вызывает ее временное изменение, после чего при восстановлении нормальных условий происходит спонтанное возвращение - к стабильному состоянию. И только более устойчивые изменения могут привести к возникновению нового стабильного распределения возрастов. Лекция 17. Популяционная экология II Потенциальная скорость естественного роста популяции. Когда среда не оказывает ограничивающего влияния (пространство, пища, другие организмы не являются лимитирующими факторами), специфическая скорость роста (т. е. скорость роста популяции на особь) для данных микроклиматических условий постоянна и максимальна. В этих благоприятных условиях скорость роста характерна для некоторой специфической возрастной структуры популяции и служит единственным показателем наследственно обусловленной способности популяции к росту. Рост популяции в нелимитированной среде при специфических физических условиях описывает следующее дифференциальное уравнение: dN/dt =rN, где параметр r можно охарактеризовать как мгновенную скорость роста популяции. Показатель r - это фактически разность между специфической мгновенной скоростью рождений (т. e. рождаемостью в единицу времени на одну особь) и специфической мгновенной скоростью гибели организмов и может быть выражен в виде: r = b – d Общая скорость роста популяции в отсутствие лимитирующего влияния среды (r) зависит от возрастного состава и вклада в репродукцию различных возрастных групп. Таким образом, вид может характеризоваться несколькими величинами r в зависимости от структуры популяции. Когда устанавливается стационарное и стабильное распределение возрастов, специфическую скорость роста называют показателем потенциального роста популяции или rmax. Часто эту максимальную величину r называют иначе - биотический или репродуктивный потенциал. Разность между rmax, или биотическим потенциалом, и фактической скоростью роста в данных лабораторных или полевых условиях используют как меру сопротивления среды, которая характеризует сумму всех лимитирующих факторов среды, препятствующих реализации биотического потенциала. В природных популяциях в непродолжительные периоды, когда пища имеется в изобилии, отсутствуют перенаселенность, враги и т. д., экспоненциальный характер роста проявляется нередко. В таких условиях популяция в целом увеличивается с огромной скоростью, хотя размножение каждого отдельного организма происходит при этом нисколько не быстрее, чем раньше, т. е. специфическая скорость роста остается постоянной. "Цветение" планктона, взрыв численности вредителей или рост популяции бактерий в свежей культуральной среде - примеры ситуаций, в которых рост часто бывает логарифмическим. Сравнительные данные, связанные со скоростью роста популяций некоторых насекомых и грызунов приведены в таблице 17.1. Таблица 17.1 Сравнительные данные, связанные со скоростью роста популяций некоторых насекомых и грызунов
Очевидно, такой экспоненциальный процесс не может продолжаться долго, а часто и вовсе не реализуется. Взаимоотношения с другими популяциями, а также сопротивление со стороны внешней среды очень скоро снижают скорость роста и различным образом изменяют его характер. Типы роста популяций. Характер увеличения численности популяции может быть различным, и в связи с этим выделяют различные типы роста популяций. По форме кривых роста можно выделить два основных типа: рост, описываемый J-образной или S-образной кривой. Эти два противоположных типа роста в соответствии, с особенностями разных организмов и условий среды могут различным образом сочетаться и модифицироваться. При J-образной форме кривой роста плотность быстро увеличивается по экспоненте, но затем, когда начинает действовать сопротивление среды или другой лимитирующий фактор (обычно более или менее резко), рост популяции внезапно прекращается. Этот тип роста может быть описан простым дифференциальным уравнением: с определенным пределом для N. Приведенное уравнение J-образной кривой роста представляет собой то же самое экспоненциальное уравнение, которое было рассмотрено для роста популяции в нелимитированной среде, с той лишь разницей, что величина N имеет в нем предел; это означает, что относительно неограниченный рост внезапно останавливается, когда популяция исчерпывает свои ресурсы (пища, жизненное пространство), когда наступают внезапные заморозки или вмешивается другой сезонный фактор или когда внезапно заканчивается сезон размножения (например, при переходе к диапаузе). После того как верхний предел для N окажется достигнутым, плотность может либо некоторое время оставаться на этом уровне, либо, как это часто случается, сразу же резко падает (рис. 17.1, А), в связи с чем отмечаются "релаксационные осцилляции". По-видимому, они характерны для природных популяций многих организмов, таких, как "зацветающие" водоросли, однолетние растения, некоторые насекомые и др. 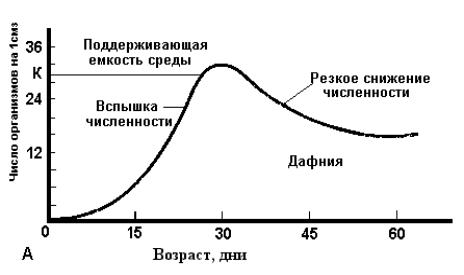 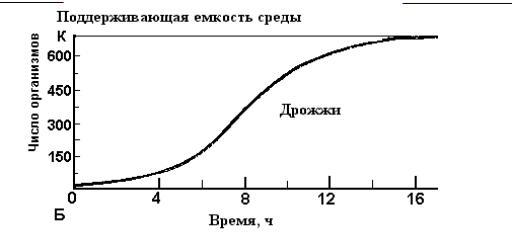 Рис. 17.1. Два типа кривых роста популяции. (А) - J-образная кривая роста дафний в культуре. Регуляция роста не связана с плотностью популяции до самого момента катастрофы. (Б) - Сигмоидная (S-образная) кривая роста дрожжей в культуре. Поддерживающая емкость среды определяется изначальным количеством доступных питательных веществ, содержащихся в среде. Сопротивление среды (в данном случае вредные факторы, обусловленные жизнедеятельностью самих организмов) линейно зависит от плотности. При описываемом S-образной кривой росте увеличение популяции вначале происходит медленно (начальная фаза, или фаза положительного ускорения), затем быстрее (фаза приближения к логарифмическому росту), но вскоре под влиянием сопротивления среды рост популяции постепенно начинает замедляться (фаза отрицательного ускорения). Это замедление по мере увеличения сопротивления становится все более выраженным, и в конце концов достигается и начинает поддерживаться более или менее устойчивое равновесие (рис.17.1, Б) . Характерная форма S-образной кривой обусловлена постепенным усилением действия неблагоприятных факторов по мере увеличения плотности популяции; в этом отношении такой тип роста является прямой противоположностью ранее рассмотренному, при котором популяция начинает испытывать сопротивление среды почти в конце своего роста. В простейшем случае усиление действия неблагоприятных факторов в зависимости от плотности является линейным. О таком простом, или "идеальном", росте говорят, что он является логическим или удовлетворяет логистическому уравнению; Дифференциальная форма логистического уравнения приведена ниже: dN/dt =rN(K- N)/K где dN/dt - скорость роста популяции (изменение численности во времени); r -специфическая скорость роста, или показатель потенциального роста; N - величина популяции (численность); K - максимальная возможная величина популяции, или "верхняя асимптота"; Приведенное уравнение отличается от экспоненциального уравнения, характеризующего рост популяции в нелимитированной среде, лишь тем, что оно содержит выражение (K - N)/K или (1-N/K). Эти последние выражения представляют собой два разных показателя, характеризующих сопротивление среды, создаваемое вследствие роста популяции, который по мере приближения к пределу вызывает все большее уменьшение скорости потенциальной репродукции. Выраженные в словесной форме, эти уравнения означают следующее:
Таким образом, описанная модель роста основывается на трех компонентах: константе скорости роста r, показателе величины популяции N и показателе влияющих на популяцию лимитирующих факторов 1- N/K. Простая ситуация, когда сопротивление среды возрастает линейно при увеличении плотности, по-видимому, имеет место только в популяциях организмов с простым жизненным циклом, например дрожжей, растущих в ограниченном пространстве, как это происходит в культуре. В популяциях более высокоорганизованных растений и животных, обладающих сложными жизненными циклами и длительными периодами индивидуального развития, изменения отсрочены во времени, в результате чего характер роста модифицируется. В таких случаях кривая роста более вогнута (требуется более длительный период для того, чтобы рождаемость оказалась эффективной), причем почти всегда популяция "перескакивает" через верхнюю асимптоту, и прежде чем численность в конце концов установится на этом уровне, она претерпевает ряд осцилляций. Для описания этого типа роста предложен модифицированный вариант логистического уравнения, которое позволяет учитывать два типа временной отсрочки в реакциях популяции: 1) время, нужное для того, чтобы в неблагоприятных условиях началось увеличение численности, 2) время, нужное для того, чтобы в неблагоприятных условиях, связанных с перенаселением, начали изменяться рождаемость и смертность. Обозначив эти промежутки времени соответственно, как t - t1 и t - t2, получаем: Исследование этого уравнения обнаруживает "выбросы" плотности и ее осцилляции с уменьшающейся во времени амплитудой. Иные многочисленные модификации основного логистического уравнения позволяют учесть сложные онтогенетические взаимодействия, характерные для высших организмов, конкуренцию, метаболические изменения в среде и общественные взаимодействия. Таблица 17.2 | ||||||||||||||||||||||||||||||||||||||
