римское право. Литература по гуманитарным и социальным дисциплинам для высшей школы и средних специальных

• Название: Литература по гуманитарным и социальным дисциплинам для высшей школы и средних специальных
• Анкор: римское право
• Дата: 14.12.2022
• Размер: 6.24 Mb.
• Имя файла: Avtonomov_V__Ananin_O__Makasheva_N_-_Istoria_ekonomicheskikh_uch.doc
• Тип: Литература; #845020
• страница: 22 из 74

3. Теория общего равновесия в XX в.:

вклад А, Вальда, Дж. фон Неймана, Дж. Хикса,

К. Эрроу и Ж. Дебре

В развитии теории общего равновесия в XX в. можно, хотя и с определенными оговорками, выделить два направления. Первое, ко торое условно можно назвать микроэкономическим, связано с и mi

Б инарность означает, что избыточный спрос на один товар уменыи.н ся точно на ту же сумму, на какую увеличился избыточный спрос на др>1 < ■ В случае если все товары — субституты и происходит бинарный сдвиг cnpuiiil оттовара J KTOBapv2, цены всех товаров относительно цены 1 возрастут iifitfl останутся неизменными, но никакое увеличение цены не будет большим,! чем увеличение цечы товара 2.

224

кмм А. Вальда, Дж. фон Неймана, Дж. Хикса, М. Алле, К. Эрроу и (, Добре¹⁰. Исследования в рамках данного направления сконцент-яроиались вокруг различных аспектов проблемы существования рав­новесия; наиболее заметные достижения были сделаны в период с jtrrw 20-х до начала 60-х годов.

Второе направление — условно макроэкономическое — возникло jttvc влиянием общего интереса к макроэкономическим проблемам и ■режде всего к проблемам безработицы и денег, анализ которых нераз-iliti [о связан с важнейшей для представителей этого направления ме-йдологической проблемой - соотношение между макро- и микропод-11ми. Называя тех, кто внес вклад в развитие этого направления, г;ловно, следовало бы начать с Дж.М. Кейнса, который, хотя и яв-•л в определенном смысле ниспровергателем равновесного подхо-федопределил проблематику будущих исследований, в том числе >бласти теории равновесия. Среди ученых, которых можно отнес-данному направлению, следует назвать О. Ланге, Д, Патинкина, шуэра, Р. Бэрроу, Г. Гроссмана. Междууказанными направлениями ■ icraeT некоторая область общих интересов, связанная с проблема­ми неопределенности, ожиданий, ограниченности информации и т.д. Строгий анализ общего равновесия начал А. Вальд. В серии ста-||< и наиболее известная из которых была опубликована в 1936 г.¹¹, он j/i.i i строгое определение равновесия и математически доказал суще-ш питание конкурентного равновесия для некоторых моделей, Ины-1м и словами, он показал, что при некоторых условиях в системе типа ||< 1'м.раса существует такой вектор неотрицательных цен, что равен-.■I I., i спроса и предложения, которое устанавливается в результате дей-■ии производителей и потребителей, максимизирующих свои це-|||гпые функции, исходя из этих цен, определит именно эти цены.

Вальд также попытался исследовать проблему единственности ре-llk-ния и выдвинул в качестве альтернативных условий существования ш;|С>ую аксиому о выявленных предпочтениях¹² для рыночных функ>

¹ К списку этих знаменитых экономистов, среди которых пять лауреа-4)11 Нобелевской премии, можно добавить Г. фон Штакельберга, Г. Нейзера Плодотворно работавших в этой области в 30-е годы.

" Wald A. Uber einige Gfeichungssysteme der mathematischen Okonomie// li-iischriftfurNationatokonotnie 1936, 7(5).

¹¹Идея выявленных предпочтений принадлежит Самуэльсону и связана с Попыткой обойтись без явного задания функции полезности и построить тео­рию спроса на основе простого наблюдения поведения потребителя. Базис­ный постулат — слабая аксиома выявленных предпочтений. Суть ее состоит в dm, что если потребитель, располагающий некоторым доходом, при некото-И)\1 векторе цен предпочел набор товаров А набору В, то и при другом векторе Ьг11 он выберет набор А, если только будет в состоянии его приобрести.

Исюряя экономкческих учений

225

ций спроса (суммы индивидуальных функций спроса для каждого то вара) и условие валовой субституции всех товаров (т.е. dEjdp > 0 для всех i^j). Оба эти условия стали центральной темой всех последую­щих работ в данной области. Доказательство достаточности последнс го условия было предложено в 1943 г. М. Алле.

Другим заметным достижением этого периода было доказательст­во существования равновесной траектории для пропорционально рас ширяющейся экономики, предложенное в 1937 г. Дж. фон Нейманом". Эта работа замечательна не только тем, что понятие равновесия в неи было использовано применительно к изменяющейся экономике, но и тем, что впервые при доказательстве существования равновесия был использован инструментарий теории игр. Тем самым был обозначен альянс теории общего равновесия и теории игр, основанный на том факте (который, однако, был строго доказан значительно позже), что модель типа Вальраса можно трактовать как игру, а следовательно, по иск равновесия есть не что иное, как нахождение решения игры.

В экономике существуют два товара, которые создаются в ходе двух производственных процессов и полностью в них потребляются (отсутствует конечное потребление). Каждый производственный про цесс характеризуется определенным уровнем интенсивности, коэф­фициенты затрат и выпуска соответствуют единичному уровню его интенсивности.

Условия сбалансированности задаются следующим образом.

Для каждого товара агрегированный выпуск должен быть не мень­ше, чем затраты, необходимые, чтобы процесс продолжался в следу­ющем периоде в расширенном масштабе:

(I)

b^ + b^Xl+giia^ + a^),

b_3]X_l + b₂₂X₂>(l+_g)(a,₁X_l+ a₁₂X₂),

где а — затраты /-го товара в процессе/ на единицу выпуска, Ь_: - вы пуск товара ;' в процессе,/ на единицу затрат, X — интенсивность про цесса/, g — темпы роста, г— процент.

Для каждого производственного процесса издержки сучетом про цента должны быть не меньше, чем получаемый доход, так как в про тивном случае соответствующий процесс расширяется, вызывая и t менение структуры цен

(II)

(1 + r)(a_lip_l+ а_2[р₂) > b_np_t + b_2]p₂, (] + г)(а_пр₁ + а_пр₂) > b_l2p_]+ Ь_пр_т

^п Упрощенный вариант модели фон Неймана представлен в khJ Niehans J. A History of Economic Theory. Classic Contributions. 1720— 1? Baltimore, L., 1990. P. 401-403.

2S6

Вопрос в том, существуют ли интенсивность производственных процессов, уровень цен, процента и темп роста, удовлетворяющие л пум группам условий, и каково их экономическое содержание?

Нейман доказал, что при некоторых условиях решение существу-п, причем максимально возможный темп роста равен минимально допустимому проценту, т.е. maxg= min r.

Это означает, что если выбран некий g, и для некоторых товаров условия (I) нарушаются, то требуется уменьшать g до тех пор, пока дня всех товаров эти условия не будут выполняться, причем для како­ю-то (одного или нескольких товаров) как равенство. Этот товар (или несколько товаров) и будет экономическим, т.е. иметь положитель­ную цену. Темп роста производства будет в этом случае максималь­ным из возможных.

Если г зафиксирован на очень низком уровне, многие процессы оказываются прибыльными - условия (II) нарушаются. Повышая г, можно добиться ситуации, когда для всех процессов условия будут иыполняться, причем по крайней мере для одного процесса - как ра-iiL-иство. Определенный в этом равенстве г и будет минимальным из допустимых.

Нейман показал, что модель расширяющейся экономики может 4>лктоваться как игра двух участников с нулевой суммой, один из гметников которой максимизирует выигрыш — темп роста эконо­мики при ограничениях на предложение, а другой — минимизирует проигрыш — процент при ограничениях на прибыль. Он доказал, что при некоторых условиях существует седловая точка (решение) такой и i ры, характеризующаяся равенством значений обеих целевых функ­ции - темпа роста и процента. Это и есть точка равновесия, задаю­щая траекторию сбалансированного роста.

Полученный фон Нейманом результат позволяет осознать важ-1М.1Й аспект равновесия, который не был выявлен в модели Вальраса, .1 именно: равновесие — это максимум выпуска в денежном выраже­нии и минимум доходов факторов. Этот вывод представляет собой ныраженное другим языком утверждение Смита о равенстве стоимо-i i и произведенной продукции и суммы доходов в экономике.

Теория игр открыла новые способы доказательства существова­ния равновесия в моделях типа Вальраса и анализа ситуаций, кото-рис традиционный равновесный подход исключал из рассмотрения. М.нав с простого случая так называемых антагонистических игр с шумя участниками, когда проигрыш одного является выигрышем Ч'угого, теория игр постепенно перешла к анализу более сложных i пгуаций -неантагонистических игр с л участниками. Применитель­но к миру экономики это, в частности, означает отказ от идеи, со-

227

гласно которой цены на рынке не зависят от поведения отдельног участника. Иными словами, игровой лодход позволяет перейти от¹ мира атомизированных и не влияющих на рынок индивидов к более реалистичной ситуации, когда от каждого участника зависит рыноч ная ситуация, например, как в случае олигополии.

Важную роль в совершенствовании методов доказательства суще ствования равновесия сыграла теорема Какутани о неподвижной точ к* (1941), которая, в частности, позволила предложить элегантную иллю страцию процесса «tatonnement» на языке современной математики"

В середине 50-х годов, основываясь на этой теореме, а также hl пользуя достижения в области линейного программирования, ряд ученых и прежде всего нобелевские лауреаты К. Эрроу (1972) и Ж. Де-бре (1983) предложили более простые и общие, чем у Вальда, теорс мы существования единственного и экономически значимого решс ния модели Вальраса. Модель Эрроу—Дебре (1954) является класс» ческой в области современной теории общего равновесия¹¹. Она пред­ставляет собой модифицированный вариант модели Вальраса, в к» торую включено множество производственных возможностей вмес­то фиксированных производственных коэффициентов, а вместо функций полезности, обладающих хорошими свойствами, введены функции предпочтения.

В модели Эрроу-Дебре фирмы трансформируют затраты в вы­пуск, причем кривые трансформации выпуклы, отсутствует эконо­мия на масштабах; домашние хозяйства предлагают труд и потребля­ют положительное количество товаров; их выбор определен функци­ей полезности, у которых кривые безразличия выпуклы; у домашних хозяйств есть положительное количество каждого товара и они пре-1 тендуют на некоторую долю прибыли.

При этих предпосылках они доказали, что существует конкурент-1 ное равновесие, которое они определили следующим образом:

максимум прибыли при заданных ценах;

максимум полезности при заданных ценах и долях в прибылях;

цены неотрицательны;

если существует избыточное предложение товара, его цена равн^ нулю.

^{1 4}Суть этой теоремы состоит в следующем: если к компактному и вь пуклому множеству применяется полунепрерывное сверху точечное отобрав жемие этого множества в себя, то по крайней мере одна точка этого множе­ства останется неподвижной, т.е. совпадет со своим отображением. Очевид» но, что именно эта неподвижная точка и будет точкой равновесия.

^is Arrow К., Debreu G Existence of an Equibibrium for a Competitive^ Economy//Econometrica. 1954 Vol. 22. № 2.

228

. При доказательстве георемы Эрроу и Дебре использовали теоре-Нэша о решении игры с п участниками и показали эквивалент-Всть понятий конкурентного равновесия и равновесия игры с п уча-Шиками.

Существовали и несколько иные подходы к доказательству рав-'шссия в модели Вальраса. Так, Л. Маккензн использовал при дока-1111^чльстве теоремы Эрроу-Дебре теорему о неподвижной точке и, что >бенно важно, предложил достаточно простую интерпретацию про­са поиска равновесия, использовав идею единичного симплекса v пространства допустимых векторов цен¹⁶. Процесс поиска рав-"■•чссиых цен он трактовал как отображение множества цен в себя, причем процесс отображения проходит промежуточную стадию ото-Чмжения цен в количества. Таким образом, процедура отображения ' i иювится интерпретацией процесса «tatonnement», неподвижная и 'чка - точкой равновесия, а ее координаты — ценами равновесия.

История проблемы существования равновесия достигла своей i v гьминации, когда в 1959 г. Ж. Дебре опубликовал итоговую работу li'opuH стоимости»", где с учетом всего сделанного ранее не только i ч,1 на изложена аксиоматика системы общего равновесия и было пред-и>ж.ено доказательство существования равновесия, но и были пред-1 i шлены доказанные в 1951 г. Дебре и Эрроу теоремы благосостоя­ния, устанавливающие (однозначное) соответствие между конкурент­ным равновесием и оптимумом по Парето. Последние выводят про-ииому равновесия в новое измерение, затрагивающее этические ос-щ'ны теории равновесия (см. гл. 14).

Наряду и порой параллельно с исследованием проблемы сущест-in шания и сопряженного с ней широкого круга проблем развивался и .шилиз проблемы устойчивости. Существование равновесия ничего in- говорит о поведении системы, т.е. о ее динамических свойствах. Мштому проблема устойчивости неотделима от проблемы динами-!■ п. В самом общем виде устойчивость ассоциируется с «притяжени-i м» системы к некоторому состоянию или траектории. Самое общее мд тематическое определение устойчивости гласит: «Линия поведения i пстемы называется устойчивой, если, начавшись внутри этой обла-

■ i и, она никогда ее не покидает». Очевидно, что конкретизация это-
i >' определения может быть различной.

"' Использовать единичный симплекс возможно, поскольку у Вальраса 'фикции спроса однородны нулевой степени от цен, т.е множитель при це-" is может быть вынесен. Если каждую цену разделить на сумму всех цен, то

■ и,пученные векторы цен будут находиться внутри единичного симплекса.

¹⁷ DebreuG. Theory of VaJue: An Axiomatic Analysis of Economic Equilibrium. ..■w Haven, 1959.

229

Дж. Хикс, П. Самуэльсон, К. Эрроу, Ф. Хан, Т. Негиши, Л. Мак-кензи, X. Узава - вот неполный перечень тех, кто в разное время ис­следовал проблему устойчивости равновесия. Но начало положили ] ЗО-е годы Дж. Хикс и П. Самуэльсон¹⁸.

Хикс предложил критерий устойчивости, представлявший, пс существу, попытку формально выразить соображения, которые уже высказывались в связи с процессом «tatonnement», а именно что уве­личение цены данного товара должно вызывать уменьшение избы­точного спроса на него, причем этот прямой эффект сильнее возмож­ного вторичного эффекта, связанного с косвенным влиянием цендру-гих товаров, изменение которых было порождено изменением спро­са на них в результате изменения цены исходного товара. Хикс со­средоточил внимание на матрице, составленной из частных произ­водных функций избыточного спроса, и пришел к выводу, что глав­ные миноры этой матрицы должны иметь меняющиеся знаки, при­чем первый минор должен быть отрицательным.

Позже Самуэльсон показал, что критерий Хикса в общем случае не является ни необходимым, ни достаточным. Он подверг критике хиксианское представление об устойчивости на том основании, что оно определено по аналогии со случаем одного рынка, и предложил собственный подход к анализу устойчивости. Самуэльсон исходил \м представления об устойчивости как о «притяжении» к некоторой точ­ке, т.е. понимал ее как свойство системы возвращаться к равновес­ной траектории после изменения исходных условий. Он обратился к динамическим характеристикам процесса «tatonnement», а именно к зависимости, связывающей скорость изменения цены товара и вели­чины избыточного спроса на него. Для наиболее простого случая — когда эта зависимость линейна, т.е. может быть представлена как dp/dt= с (А ■+ Вр), где А и В — матрицы коэффициентов, р - вектор цен, он показал, что необходимым и достаточным условием устойчи­вости системы является то, что действительные части характеристи­ческих чисел матрицы В отрицательны¹⁹. Для случая одного рынка это условие эквивалентно условию Хикса.

В конце 50-х годов, используя иные методы анализа, Эрроу и дру­гие экономисты-математики сформулировали следующие альтерна-j

С м.^- Хикс Дж. Стоимость и капитал. М., 1988. Гл. 5 и Приложение i ней; SamuelsonP. The Stability of Equilibrium: Linear and Non-Linear Systems, Econometrica. 1942. Vol. 10. January. The Relation Between Hicksian Stability and True Dynamic Stability// Econometrica. 1944. Vol. 12. July—October.

¹⁹ Характеристические корни матрицы [aj - корни уравнения степени п от л, полученного для определителя матрицы \А — хГ\, где /— единичная ма­трица.

230

тивные достаточные условия устойчивости: все товары - субституты; рынки удовлетворяют слабой аксиоме о выявленных предпочтениях; якобиан (т.е. определитель матрицы, составленной из частных про­изводных функций избыточного спроса) имеет доминантную диаго-паль, все элементы которой отрицательны. Последнее условие, оче­видно, не что иное, как утверждение о том, что увеличение цены дан­ного товара ведет к уменьшению спроса на него, независимо от воз­действия других цен.

Дискуссии, о которых шла речь выше, строго говоря, касались математической стороны теории общего равновесия, экономическая интерпретация полученных результатов часто оказывалась достаточ­но затруднительной. В этом смысле более экономически содержатель­ными были исследования в рамках того направления, которое выше было обозначено как макроэкономическое.

4. Макроэкономический аспект модели общего равновесия

Экономика Вальраса представляет собой множество индивиду­альных экономических субъектов, связанных через рынок. Хотя в модели используются агрегатные показатели, например совокупный спрос на какой-либо товар, денежное выражение совокупного спро­са и т.д., все эти показатели являются простыми арифметическими производными от переменных индивидуального уровня. По своей сути модель Вальраса — микроэкономическая и натуральная, т.е. опи­сывающая экономику в терминах относительных величин — пропор­ций, так что сама постановка вопроса о ее макроэкономической ин­терпретации и о придании ей денежного измерения может показать­ся логически несостоятельной. Причем оба вопроса тесно взаимосвя­заны, так как деньги - особый товар, выражающий некоторые об­щие свойства системы.

Эту же самую проблему можно представить и иначе — как про­блему перехода от относительных цен, определенных в модели Валь­раса, к их абсолютному уровню. Применительно к этой интерпре­тации и для обозначения того обстоятельства, что определение от­носительного уровня цен (решение модели) и определение их абсо­лютного уровня (через введение дополнительного уравнения, уста­навливающего зависимость между количеством денег в экономике, с одной стороны, и общим уровнем цен и объемом сделок — с дру­гой) являются, по существу, независимыми процедурами, в совре­менной теории существует специальный термин «классическая

231

дихотомия»²⁰. Преодоление этой дихотомии связывается с макрс экономической интерпретацией теории общего равновесия и вкль чением в нее денег.

Одна из наиболее интересных попыток решения этой проблемы модель, предложенная Д. Патинкином в работе «Деньги, процент и цены» (1956, 1965)²¹ и затронувшая целый комплекс проблем, как не­посредственно связанных с теорией общего равновесия, так и постаь-ленных кейнсианской теорией (см. гл. 29).

Модель Патинкина была получена из стандартной модели обще­го равновесия простым агрегированием соответствующих функций.¹ С помощью этой модели он пытался решить проблему дихотомии и доказать устойчивость модели равновесия, допускающей вынужден­ную безработицу. Основное нововведение Патинкина, сделавшее его модель заметным явлением в современной теории, заключается в том, что деньгам была придана самостоятельная роль страхового фонда, и это послужило оправданием включения денег в форме реальных (т.е. с учетом покупательной способности) кассовых остатков в индивиду­альные функции спроса и предложения. Влияние изменения вели­чины реальных кассовых остатков на уровень индивидуального (и аг­регированного) спроса — эффект реальных кассовых остатков — ста­ло еще одним, наряду с ценами, равновесным механизмом. Суть это­го эффекта состоит втом, что субъекты стремятся поддерживать кас­совые остатки на некоем оптимальном уровне, отражающем их пред­ставления о регулярности финансовых поступлений и необходимой обеспеченности средствами обращения. Индивиды реагируют на из-менения величины своих реальных кассовых остатков, изменяя ве­личину индивидуального спроса и предложения.

Чтобы «оправдать» существование денег, Патинкин допускаа возможность несовпадения во времени платежей и поступлений, что в действительности означает отход от идеи аукциониста или, говоря

С уть проблемы состоит в том, что попытки объединить модель Валь-раса с уравнением денежного обращения оказались несостоятельными.

Если к обычной системе Вальраса добавить уравнение спроса на деньги, например, соответственно изменив балансовое тождество, то окажется, что функция спроса на деньги должна одновременно быть линейно однородной от цен и линейно однородной от цен и количества денег. Именно это фор­мальное противоречие заставило поставить вопрос о включении денег и функции спроса.

^ Patinkin D. Money, Interest, and Prices. N.Y., 1956; 2nd ed. N.Y., 1965.

Впервые идею влияния изменения стоимости накопленных активов на потребление высказал А. Пигу в работе «Занятость и равновесие» (1949). Он связывал этот эффект с так называемыми внешними деньгами — чистой задолженностью правительства частному сектору.

232

современным языком, от предпосылки о полной информированнос­ти экономических субъектов, или о мгновенной реакции цен на из­менение рыночных условий.

В самой простой модели действуют три группы участников: по­требители, предъявляющие спрос на товары и предлагающие труд, фирмы, предлагающие товары и предъявляющие спрос на труд, и го­сударство, осуществляющее эмиссию денег. Формально такая модель может быть представлена следующим образом:

Y=E(Y,M/p)

L*(W/P) = V(W/P),

где Е— совокупный спрос; Р — индекс цен; К— совокупное предло­жение (доход в натуральном выражении); М масса денег в обраще­нии; L'', L^s— спрос и предложение труда; L - уровень занятости; W— номинальная заработная плата.



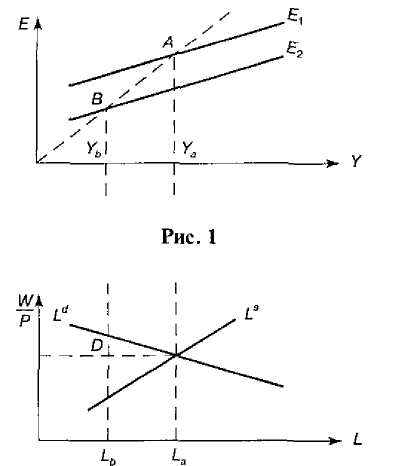
Рис.2

Графическая интерпретация модели может быть представлена следующим образом (рис. 1 и 2). Допустим, что сократился сово­купный спрос (E_tсдвигается вниз до Е₂). Точка макроэкономичес­кого равновесия перемещается из А в В. Если цены абсолютно по­движны, то можно ожидать мгновенного восстановления равнове-

233

сия на рынке товаров благодаря эффекту реальных кассовых остат ков. Но если иены недостаточно подвижны, то возникает ситуация избыточного предложения товаров, на которую фирмы реагирую) сокращением производства и спроса на рабочую силу. Эта ситуация отражается точкой D, в которой ни фирмы, ни работники не нахо дятся в положении равновесия, так как при W/Р = (ЩР)₀у фирм нарушено условие максимальной прибыли, и они будут стремиться к расширению производства, а на рынке рабочей силы возникае! ситуация избыточного предложения. Если цены и заработная плата изменяются, а объем совокупного спроса — нет, ситуация вынуж­денности сохраняется. Восстановление равновесия предполагает, во-первых, подвижность цен и заработной платы, а во-вторых, нали­чие эффекта реальных кассовых остатков, который «сдвинет» ли­нию совокупного спроса вверх. В результате прежний объем произ­водства восстанавливается, но при более низком значении номи­нальных цен и заработной платы.

Подобная модель вызвала широкую дискуссию, в ходе которой обсуждались следующие проблемы: относительной скорости реакции цен и количеств на сокращение спроса; относительной силы (направ­ленного на восстановление равновесия с полной занятостью) эффекта реальных кассовых остатков и механизма движения к равновесию при более низком уровне производства; характера ситуации вынужден­ной безработицы (относить ли эту ситуацию к равновесной или не­равновесной). Была также поставлена проблема ожиданий и связан­ная с ней проблема неопределенности.

Интерес к этим проблемам возник еще в конце 20-х годов, когда многие теоретики, стремясь преодолеть статический характер моде­ли общего равновесия, обращались к идее последовательности рав­новесных состояний, связующим звеном между которыми были ожи-дания³¹. В 1927 г. Г. Мюрдаль, развивая идеи Викселля (см. гл. 16), обратился к рассмотрению межвременного равновесия, отражающе­го влияние текущих изменений рыночной ситуации на будущие цены и, наоборот, влияние ожиданий будущих изменений на текущие цены. Он ввел понятия «ex ante» и «ex post», выражающие различия между ситуацией, которую определяют планы и ожидания, и ситуацией, которая фиксирует их реализацию, и использовал эти понятия при объяснении парадокса несовпадения совокупных инвестиций и сбе­режений, столь важного в кейнсианской модели (см, гл. 29).

^{3 1} Об исследовании роли ожиданий п модели общего равновесия см., например: Phelps E. Equilibrium: as Expectation! Concept // New Palgrave. Vol. I.L., 1989.

234

Проблема ожиданий и их влияния на текущую ситуацию, так же v ,ik и реакция экономических субъектов, прежде всего инвесторов, ил степень реализации ожиданий, была одной из центральных тем у Кгйнса. Почти одновременно эта тема прозвучала у Дж. Хикса в ра-1м>ге «Стоимость и капитал» (1939)²⁴. Хикс пытался преодолеть ста-i пчность равновесной модели и предложил модель последовательных р мшовесных состояний — так называемую «многопериодную модель», и которой особое внимание уделил взаимовлиянию настоящего и бу-чмцего через механизм ожиданий цен. Позднее в рамках этого на­правления поисков была поставлена проблема ограниченности зна­ния экономических индивидов и в связи с ней уточнялись понятия р.шновесия и рациональности.

Проблема интеграции ожиданий и расширения временного го™ рм-юнта, а в более общей формулировке проблема динамизации мо-ш равновесия была осознана и представителями первого направ-кия, занимающимися усовершенствованием классических моделей иновесия. Среди работ такого рода следует указать «многопериод-ц\ ю» модель Р. Раднера, В этой модели была использована идея сроч-и их сделок, т.е. таких, которые пересматриваются перед началом но-imio временного интервала на базе накопленной информации. Рад-iii'P показал, что с помощью такой модели можно изучать вопрос о * |>гласовании ожиданий и планов участников, а также дать более об­щее определение равновесия, включающее в числе переменных на-рмду с текущими ценами ожидания и планы участников²⁵.

Теория общего равновесия является абстрактным ответом на аб-

' фактный вопрос о том, может ли децентрализованная система, в

i и горой значима только информация, представленная ценами, быть

\ моридоченной? Теория общего равновесия дает на этот вопрос ут-

iii рдительный ответ, но не пытается ответить на вопрос, в какой мере

рг.шистична подобная система. Поэтому и эмпирическая проверка

ишотез, и обращение к историческому опыту в строгом смысле не

м<иуг давать основание для подтверждения или опровержения этой

нории, хотя многие представители указанной теории стремились

■ ч казаться от наиболее нереалистичных предпосылок. Осознавая аб-

рактный характер теории общего равновесия, нельзя не признать

юдотворности ее как инструмента решения многих проблем, часто

входящих за первоначально обозначенные рамки анализа. Нетоль-

i развитие теории общего равновесия, но и ее критика способство-

^м Хикс Дж. Стоимость и капитал. М.: Прогресс, 1988. " См.¹ Вайнтрауб Э.Р. Теория общего равновесия // Современная эко-очическая мысль М.: Прогресс, 1981.

235

вали появлению новых самостоятельных теоретических направлений Так, критика оптимизационного подхода как способа описания по ведения субъекта в условиях неопределенности стимулировала фор мирование эволюционной теории, а попытки затронуть проблему распределения дали толчок развитию экономической теории благо состояния.

Рекомендуемая литература

Негиши Т. История экономической теории. М.: Аспект-пресс, 1995. Гл.7.

Селигмен Б. Основные течения современной экономической мыс­ли. М.: Прогресс, 1968. Гл. 4.

Современная экономическая мысль. М.: Прогресс, 1981. Гл. 3.

Энтов Р. У истоков «чистой экономической теории»: Вальрас // Во просьг экономики. 1990. № 1.

Arrow К. Economic equilibrium // The New Palgrave. Vol. 1. L.: The Mac-millan Press, 1987.