мат мет-лекции-ИНТЕРНЕТ. Математические методы в психологии
 Скачать 2.19 Mb. Скачать 2.19 Mb.
|
Тема 12 Дисперсионный анализОбщие принципы дисперсионного анализаДисперсионный анализ – это анализ изменчивости признака под влиянием какого-либо фактора или совокупности факторов. Метод основан на разложении общей дисперсии (вариативности) на составляющие компоненты, сравнивая которые можно определить долю общей вариации изучаемого признака, обусловленную действием на него как регулируемых, так и неучтенных в опыте факторов. При проведении дисперсионного анализа результаты наблюдений группируются с учетом градаций влияющего фактора. Если фактор оказывает влияние на признак, средние арифметические значения результирующего признака изменяются в соответствии с градациями фактора. Внутри каждой такой группы обнаруживается своя дисперсия, связанная с действиями других факторов. Нулевая гипотеза сводится к предположению о равенстве межгрупповых средних и дисперсий (то есть, считается, что никакого систематического действия факторов на результативный признак нет, наблюдаемые различия в групповых средних являются случайными). Для принятия-отвержения отвержения нулевой гипотезы используется таблица критических значений F-критерия Фишера. При этом применяется стандартный принцип: Fэмп Fкр Н1. Дисперсионный анализ не следует путать с факторным анализом. При помощи факторного анализа мы выделяем из множества измеряемых характеристик новые факторы, скрытые ранее. Дисперсионный анализ свидетельствует о степени влияния уже известных и выделенных факторов. Принято выделять однофакторный и многофакторный виды дисперсионного анализа. В однофакторном анализе дисперсия разлагается на две составные части: дисперсию, связанную с изменением внутригрупповых средних значений и случайную дисперсию. В многофакторном – на ряд частей: дисперсии, обусловленные воздействием каждого фактора по отдельности; дисперсии, обусловленные воздействием парных сочетаний факторов; случайную дисперсию. Проведение дисперсионного анализа реализовано в программах Statistica и последних версиях Excel. Однако, как показывает практика, не каждый студент умеет ими пользоваться. Поэтому в данном пособии дан конкретный алгоритм проведения как однофакторного, так и двухфакторного дисперсионного анализа. Е.В. Сидоренко отмечает, что для проведения данного вида анализа все разряды испытуемых должны содержать одинаковое количество оптантов и результативные показатели должны подчиняться закону нормального распределения. Однако, это является хотя и желательным, но не обязательным условием Предварительно вводятся ряд специфических обозначений: SSобщ -общая сумма квадратов SSмг – межгрупповая сумма квадратов, обусловленная взаимодействием факторов. SSвг - внутригрупповая сумма квадратов, рассчитывается для каждого фактора. SSслуч – сумма квадратов соответствующая случайному рассеиванию MS – средняя сумма квадратов Однофакторный дисперсионный анализПостановка задачи: зависит ли уровень удовлетворенности профессией у учителей от длительности работы в данной сфере деятельности? В школе были отобраны 3 группы учителей (6+6+5 человек) по одному и тому же предмету, все мужчины. Принадлежность к то или иной группе зависела от стажа работы в школе. Затем была исследована методом самоотчета степень удовлетворенности профессией (максимальный показатель = 10 баллам, минимальный – 0). Данные занесены в таблицу:
Дальнейший этап - выдвижение гипотез. Но : различия между градациями фактора достоверно не превосходят случайные различия внутри группы (то есть исследуемый фактор не влияет на результативный признак). Н1 : различия между градациями фактора достоверно превосходят случайные различия внутри группы (то есть исследуемый фактор влияет на результативный признак). Затем необходимо определить объем разрядов, возвести в квадрат все значения и определить общую сумму квадратов.
Теперь необходимо произвести вычисления по следующим формулам: В указанные формулы подставляются соответствующие значения. Таблицы для определения критических значений отличаются от других таблиц (столбцы не соответствуют уровням критической значимости) и составлены по другому принципу: столбцы расположены в соответствии со степенями свободы между группами, а строки – в соответствии со степенями свободы внутри групп. В связи с этим, для фиксации критических значений рекомендуется составить следующюю таблицу:
Fэмп>Fкр (р=0,05) H1 ст.зн. 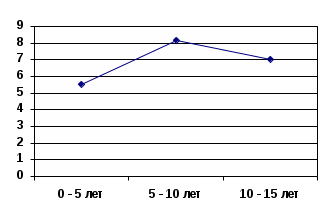 Таким образом, мы можем сказать, что исследуемый фактор (стаж работы в школе) влияет на степень удовлетворенности профессией. Для ответа на вопрос о характере этого влияния необходимо определить средние арифметические значения для каждого разряда и построить график.
При анализе гистограммы можно увидеть, что на первом этапе удовлетворенность работой педагога низка, на отрезке 5 – 10 лет она имеет максимальные значения и в последующие 5 лет несколько снижается. |
