мат мет-лекции-ИНТЕРНЕТ. Математические методы в психологии

• Название: Математические методы в психологии
• Дата: 01.06.2022
• Размер: 2.19 Mb.
• Имя файла: мат мет-лекции-ИНТЕРНЕТ.doc
• Тип: Документы; #561290
• страница: 18 из 35

Тема 9 Оценка достоверности различий

t-критерий для несвязанных (независимых) измерений

Для оценки достоверности различий в выборках, то есть фактически для их сравнения, при работе с данными, измеренными в метрических шкалах, чаще всего используют t-критерий Стьюдента. Это мощный параметрический критерий, дающий достоверные результаты даже если выборка мала. Данный критерий встречается в 2-х вариантах: для связанных выборок (о нем речь пойдет в следующем разделе) и для несвязанных. При работе с обоими вариантами критерия используется одна и та же таблица критических значений, но формулы расчета отличаются.

Формула t-критерий Стьюдента для несвязанных выборок имеет следующий вид: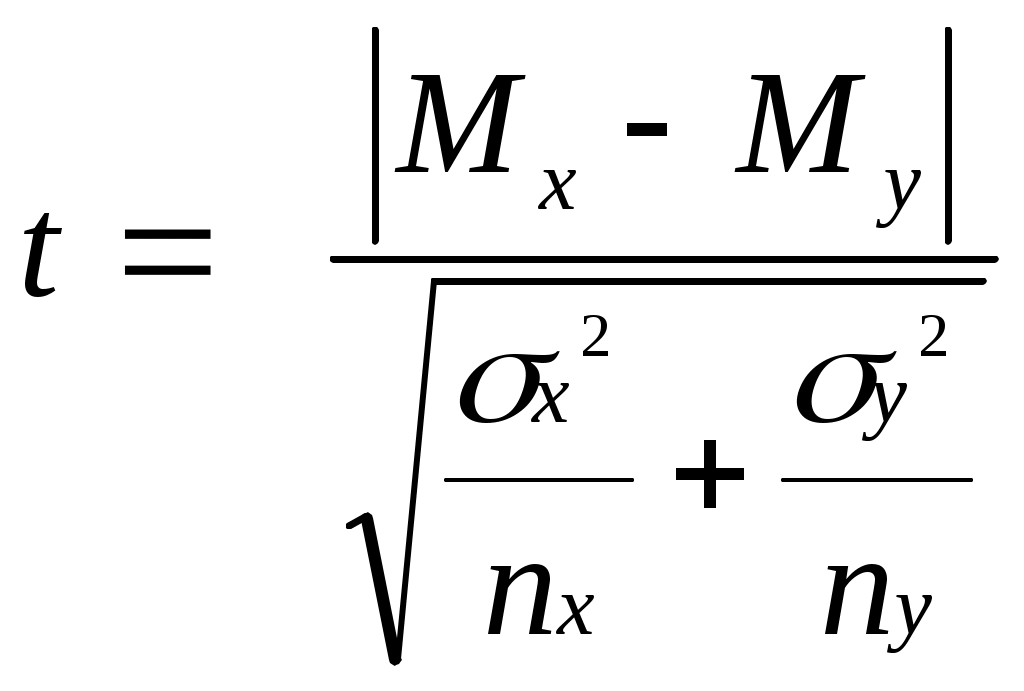



Допустим, школьники в двух разных классах в течение года занимались по двум различным методикам. Известно, что начальный уровень в этих классах был примерно одинаков. В конце учебного года были сделаны замеры показателей интеллекта. Насколько различается уровень умственного развития в этих двух классах? Данные заносятся в таблицу.

	Класс А	Класс Б
n	24	20
M	108	101
	10	11

Гипотезы:

Н₀: достоверность различий между показателями интеллекта у школьников класса А и класса Б значимо не отличается от нуля.

Н₁: достоверность различий между показателями интеллекта у школьников класса А и класса Б значимо отличается от нуля.

Подстановка значений в формулу дает следующий результат: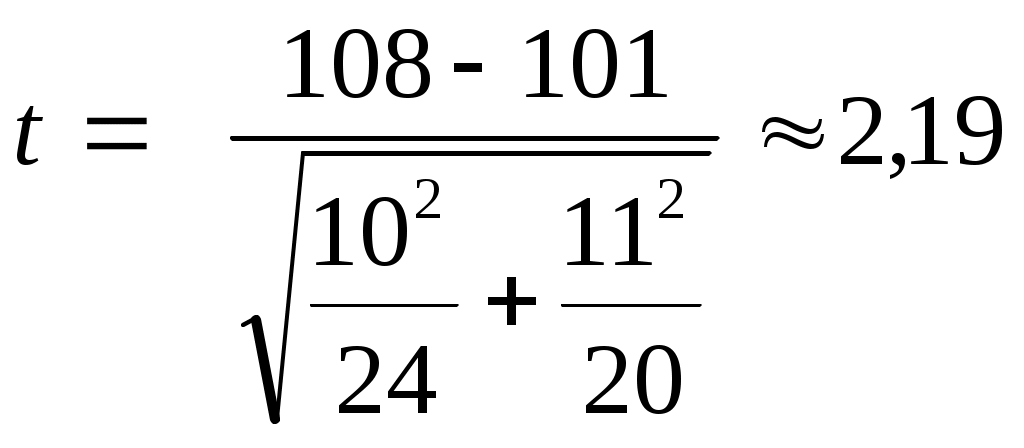



Для того, чтобы воспользоваться таблицами критических значений необходимо вычислить степень свободы. Для данного критерия df= n₁+n₂-2. У нас df = 42.

df	р = 0,1	р = 0,05	р = 0,01	р = 0,001
42	1,682	2,018	2,698	3,538

Эмпирическое значение занимает промежуточное положение между р-уровнями р = 0,05 и р = 0,01. Таким образом, t_эмп > t_кр (p ≤ 0,05) H_0,  Н₁! ст. зн.

Мы можем уверенно опровергнуть нулевую гипотезу и констатировать, что обнаружена достоверность различий на уровне статистической значимости.

U-критерий Манна-Уитни

Непараметрический U-критерий Манна-Уитни позволяет оценить достоверность различий в независимых выборках, если данные в них представлены в ранговой шкале. Данный критерий следует применять и в том случае, если данные представлены в метрических шкалах, но не укладываются в кривую нормального распределения. При этом следует обратить на ограничения в использовании критерия: в каждой выборке должно быть не менее 3 и не более 60 наблюдений.

Обе выборки объединяются, осуществляется ранжирование по принципу «меньшему значению – меньший ранг», затем объединенная выборка снова расщепляется, но с сохранением значений рангов присвоенных при объединенном ранжировании.

В качестве примера предлагается проанализировать первые 20 значений из Таблицы I Приложения с целью выяснить: существуют ли для мальчиков и девочек достоверные различия между результатами субтестов на осведомленность.

Формулируются статистические гипотезы.

Н₀: разница между показателями субтеста осведомленности у мальчиков и девочек значимо не отличается от нуля.

Н₁: разница между показателями субтеста осведомленности у мальчиков и девочек значимо отличается от нуля.

Исходная таблица			Ранжирование	объединенной	выборки
пол	осведомленность		пол	осведомленность	Ранг
ж	12		ж	7	1
ж	10		ж	8	2
м	11		м	9	3,5
ж	14		м	9	3,5
ж	12		ж	10	5,5
ж	10		ж	10	5,5
м	9		м	11	7,5
ж	14		м	11	7,5
ж	14		ж	12	10
ж	15		ж	12	10
ж	13		м	12	10
м	9		ж	13	12,5
ж	16		м	13	12,5
ж	14		ж	14	16
м	11		ж	14	16
ж	7		ж	14	16
м	13		ж	14	16
ж	8		м	14	16
м	12		ж	15	19
м	14		ж	16	20

Повторное расщепление с сохранением рангов и подсчет ранговых сумм

Осв М	Ранг М	Осв Ж	Ранг Ж
14	16	16	20
13	12,5	15	19
12	10	14	16
11	7,5	14	16
11	7,5	14	16
9	3,5	14	16
9	3,5	13	12,5
		12	10
		12	10
		10	5,5
		10	5,5
		8	2
		7	1
	м = 60,5		ж = 149,5

Значение U определяется по формуле:



где n₁ – объем первой выборки;

n₂ – объем второй выборки;

Т_х – большая из ранговых сумм;

n_x – объем группы с большей суммой рангов.

В нашем случае U_эмп = (13*7) + - 149,5 = 32,5

Согласно таблицам критических значений, при n₁=13 и n₂=7, U_кр (для p ≤ 0,05) = 20 и U_кр (для р ≤ 0,01) = 13.

Критерий Манна-Уитни отличается от большинства других критериев тем, что для опровержения нулевой гипотезы эмпирическое значение должно быть меньше или равно критическому (подобная закономерность типична также для Т-критерия Вилкоксона и критерия знаков G). То есть, используется следующий принцип: U_эмп ≤ U_кр  Н₁!

В нашем случае U_эмп = 32,5. То есть, U_эмп ≥ U_кр (p ≤ 0,05)  Н₀! Таким образом, достоверность различий между показателями осведомленности у мальчиков и у девочек не установлена.

Задания для самостоятельной работы.

1. 
   Определить достоверность различий между показателями среднего балла интеллекта у мальчиков и у девочек. Значения брать из Таблицы I Приложения. Использовать t-критерий Стьюдента.
   
2. 
   Определить достоверность различий между показателями успеваемости у мальчиков и у девочек. Значения брать из Таблицы I Приложения. Использовать t-критерий Стьюдента.
   
3. 
   Определить достоверность различий между показателями субтеста «арифметика» у мальчиков и у девочек. Значения брать из Таблицы I Приложения. Использовать U-критерий Манна-Уитни.
   
4. 
   Определить достоверность различий между показателями субтеста «понятливость» у мальчиков и у девочек. Значения брать из Таблицы I Приложения. Использовать U-критерий Манна-Уитни.