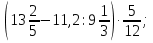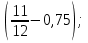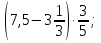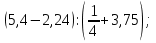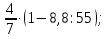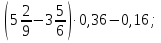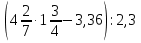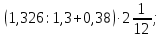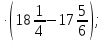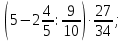ВСР математика. Методические рекомендации по выполнению внеаудиторной самостоятельной работы по дисциплине оуд. 04 Математика алгебра и начала математического анализа геометрия для студентов I курса
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЕЖИ РЕСПУБЛИКИ КРЫМ ГБПОУ РК «КЕРЧЕНСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
Методические рекомендации по выполнению внеаудиторной самостоятельной работы по дисциплине ОУД.04 Математика: алгебра и начала математического анализа; геометрия для студентов I курса специальность: 15.02.08 Технология машиностроения 38.02.01 Экономика и бухгалтерский учет (по отраслям) 15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям) 21.02.05 « Земельно-имущественные отношения» 40.02.01 «Право и организация социального обеспечения»
Пояснительная записка Методические указания являются составной частью учебно-методического комплекса дисциплины ОУД.04 Математика: алгебра и начала математического анализа; геометрия, содержат рекомендации по ее самостоятельному изучению, имеют целью дать учащимся углубленное понимание математики и научить сознательно пользоваться основными понятиями, формулами, законами, теоремами при решении практических задач. При самостоятельной работе над учебниками и учебными пособиями рекомендуется придерживаться определенной последовательности. Читая и конспектируя тот или иной раздел учебника, необходимо твердо усвоить основные определения, формулы, теоремы, которыми определяется связь и зависимость одних величин от других. Формулировки законов и методику вывода их математических выражений надо знать на память. После усвоения соответствующих понятий и закономерностей следует решить примеры и задачи, закрепляя тем самым проработанный теоретический материал, а затем приступить к решению задач. Изучая материал по учебнику, следует переходить к следующему вопросу только после правильного понимания предыдущего, проделывая на бумаге все вычисления (в том числе и те, которые по их простоте опущены в учебнике), воспроизводя имеющиеся в учебнике чертежи. Особое внимание следует обратить на определение основных понятий. Студент должен подробно разобрать примеры, которые поясняют такие определения, и уметь привести аналогичные примеры самостоятельно. Необходимо помнить, что каждая теорема состоит из предположений и утверждения. Все предположения должны обязательно использоваться в доказательстве. Нужно добиваться точного представления о том, в каком месте доказательства использовано каждое предположение теоремы. Полезно составлять схемы доказательства сложных теорем. Правильному пониманию многих теорем помогает разбор примеров математических объектов, обладающих и не обладающих свойствами, указанными в предположениях и утверждениях теорем. Письменное оформление работы имеет важное значение. Записи в конспекте должны вестись аккуратно, поскольку это не только приучит студентов к необходимому порядку в работе, но и позволит избежать многочисленных ошибок, происходящих из-за небрежных, беспорядочных записей. Выводы, полученные в виде формул, рекомендуется подчеркивать или обводить рамкой, чтобы они выделялись и лучше запоминались. При решении задач нужно обосновывать каждый этап, исходя из теоретических положений. Если существует несколько способов решения, то необходимо выбрать самый удобный. Решения задач и примеров необходимо записывать подробно, вычисления располагать в строгом порядке, отделяя вспомогательные вычисления от основных. Ошибочные записи следует не стирать или замазывать, а зачеркивать. Чертежи необходимо выполнять аккуратно и в соответствии с данными условиями. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие, и по возможности в общем виде с выводом формулы, в которую затем подставить числовые значения (если они даны) входящих в нее величин. В промежуточные вычисления не следует вводить приближенные значения корней, числа π и т. д. Полученный ответ следует проверять способами, вытекающими из смысла задачи или же решить ее несколькими способами и сравнить результаты. Если студент не разобрался в теоретическом материале, он может обратиться к преподавателю за консультацией, указав, в каком учебнике и на какой странице рассмотрен затрудняющий его вопрос, и что именно его затрудняет. Если же затруднение вызвало решение задачи, то следует указать характер этого затруднения и привести предполагаемый план решения. Памятка 1. Решение задач по теме. Цели работы: учиться использовать основные алгоритмы для решения задач по теме, учиться анализировать условие задачи, сопоставлять его с изученными алгоритмами и выбирать из них необходимый, использовать математический язык для записи выполненных заданий, учится контролировать качество выполнения работы, учиться планировать и контролировать время на выполнение работы. Прочтите тему работы и предложенные задания. Ознакомьтесь со сроками сдачи работы и с критериями оценивания. Ознакомившись с задачами, подберите алгоритмы их решения (из конспекта лекции, практического занятия, основного учебника). При решении задач используйте формы записи, предложенные в лекциях и в аудиторных практикумах. Работу выполняйте в тетради для домашних заданий, записывая задания в том порядке, в котором они предложены в тексте работы. Все вычисления, выполняемые вручную, записывайте в тетради. Подготовьте вопросы по тем заданиям, которые вызвали у Вас затруднения, для консультации с преподавателем. Проанализируйте, какую отметку вы можете получить в соответствии с предложенными критериями оценивания. Не бросайте трудные или непонятные, на первый взгляд, задачи. Постарайтесь найти аналогичные задания в лекциях, практических занятиях или учебнике. Работу сдавайте в указанный срок. Памятка 2. Составление конспекта по теме. Цели работы: учиться выделять главное по теме в учебной и научной литературе, учиться структурировать отобранный материал, использовать математический язык для записи отобранного материала, контролировать качество выполнения работы, планировать и контролировать время на выполнение работы. Прочтите предложенный материал по указанному источнику. Ознакомьтесь со сроками сдачи работы и с критериями оценивания. Выделите ключевые вопросы (основные формулы), рассмотренные в тексте по данной теме. Ознакомьтесь с вопросами по предложенной теме. Выпишите только то, что считаете необходимым. Не забывайте, что составить конспект – это не списать текст из источника, а отобрать главное! Если составляете таблицу с формулами, обдумайте, какие формулы боле важные, их выпишите в первую очередь! Проверьте, содержит ли Ваш конспект ответы на все поставленные вопросы (все необходимые формулы). Проанализируйте, какую отметку вы можете получить в соответствии с предложенными критериями оценивания. Работу сдавайте в указанный срок. Памятка 3. Реферат (письменный доклад), сообщение по теме. Цели работы: учиться отбирать источники информации в соответствии с выбранной темой, учиться выделять главное по теме в отобранных источниках информации, учиться структурировать отобранный материал, использовать математический язык для записи отобранного материала, учится контролировать качество выполнения работы, учиться планировать и контролировать время на выполнение работы.
Приложение. Оформление титульного листа МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЁЖИ РЕСПУБЛИКИ КРЫМ ГБПОУ РК «КЕРЧЕНСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ» РЕФЕРАТ по дисциплине: « Математика» «_______________________________» тема
г. Керчь 20___ г. Критерии оценивания
Перечень тем, которые выносятся на самостоятельное изучение
Раздел 1. Развитие понятия о числе. ВСР 1. «Действия над рациональными числами. Преобразование алгебраических, рациональных, иррациональных выражений». Цель: Уметь выполнять действия над рациональными числами, преобразования алгебраических и рациональных выражений Методические рекомендации: Алгебраическим выражением называется совокупность конечного количества чисел, обозначенных буквами или цифрами, соединенных между собой знаками алгебраических действий и знаками последовательности этих действий (скобками). Алгебраическое выражение, в котором указаны только действия сложения, вычитания, умножения и возведения в степень с натуральным показателем, называют целым рациональным выражением. Если кроме указанных действий входит действие деления, то выражение называют дробно-рациональным. Целые рациональные и дробно-рациональные выражения вместе называются рациональными. Если входит еще и действие извлечения корня, то такое выражение называют иррациональным. При выполнении данной работы необходимо вспомнить основное свойство дроби и действия над дробями: 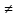 0, с 0, с 0; 0;При решении примеров на совместные действия с обыкновенными и десятичными дробями часть действий можно выполнять в десятичных дробях, а часть - в обыкновенных. Надо иметь в виду, что не всегда обыкновенная дробь может быть превращена в конечную десятичную дробь. Поэтому записывать десятичной дробью можно только тогда, когда проверено, что такое преобразование возможно. Умножение десятичных дробей. Чтобы перемножить две десятичные дроби, достаточно, не обращая внимания на запятые, перемножить их как целые числа и в произведении отделить запятой справа столько десятичных знаков, сколько их было во множимом и множителе вместе. Деление десятичной дроби на целое число выполняется так же, как и деление целых чисел; получаемые остатки раздробляют последовательно в меньшие десятичные части и продолжают деление до тех пор, пока в остатке будет нуль.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||