Литература:
Письменный Д.Т. Конспект лекций по высшей математике: полный курс. - Москва: Айрис-пресс, 2002, ( . .
Яковлев Г.Н. Математика для техникумов. Геометрия. - Москва: Наука, 1982, ( . .
Раздел 8. Прямые и плоскости в пространстве
ВСР 27. Опорные факты планиметрии. Аксиомы планиметрии. Углы и параллельные прямые
Цель: Повторить опорные факты планиметрии, aксиомы планиметрии, виды углов и свойства параллельных прямых
Методические рекомендации:
I. Изучить теоретический материал и письменно ответить на вопросы, выполнить рисунки с обозначениями:
Что такое геометрия?
Что такое планиметрия?
Что такое аксиома?
Что такое теорема?
Назовите основные фигуры планиметрии
Сформулируйте основное свойство принадлежности точек и прямых
Сформулируйте основное свойство расположения точек на прямой
Сформулируйте основное свойство измерения отрезков
Сформулируйте основное свойство расположения точек относительно прямой
Сформулируйте основное свойство измерения углов
Сформулируйте основное свойство откладывания отрезков
Сформулируйте основное свойство откладывания углов
Сформулируйте основное свойство параллельных прямых
Что такое луч?
Что такое отрезок?
Что такое угол?
Перечислите виды углов
Какие прямые наз. параллельными?
Какие углы называют смежными?
Сформулируйте основное свойство смежных углов
Какие углы называют вертикальными?
Сформулируйте основное свойство вертикальных углов
Какие прямые наз. перпендикулярными?
Что такое биссектриса угла?
Сформулируйте свойства параллельных прямых
Какие углы называют внутренними накрест лежащими?
Какие углы называют внутренними односторонними?
Какие углы называют соответственными?
Сформулируйте признак параллельности прямых
Литература:
А.Д. Александров, Геометрия 10 кл., М.: Просвещение, 2014
Л.С. Атанасян, Геометрия 10-11, М.: Просвещение, 2014
Погорелов А.В. Геометрия: Учебник для 7-11классов средней школы.- Москва: Просвещение, 1993
ВСР 28. Треугольники, окружность. Четырехугольники, многоугольники
Цель: Повторить определения, основные свойства и формулы, изученные по указанным темам в школе
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы, выполнить рисунки с обозначениями:
Что такое треугольник
Виды треугольников (в зависимисти от углов, от сторон).
Какие треугольники равны?
Сформулируйте теорему о сумме углов треугольника.
Что такое внешний угол треугольника и каким свойством он обладает?
Как называются стороны прямоугольного треугольника?
Что такое высота, медиана ,биссектриса треугольника?
Какой треугольник называют равнобедренным? Его свойства.
Какой треугольник называют равносторонним? Его свойства
Сформулируйте признаки равенства треугольников
Сформулируйте признаки подобия треугольников
Запишите формулы вычисления площади треугольника
Что такое окружность? Радиус, диаметр?
Дайте определение касательной к окружности
Запишите формулы длины окружности
Дайте определение круга
Запишите формулу вычисления площади круга
Дайте определение кругового сектора
Дайте определения окружности, вписанной в треугольник, и описанной около треугольника. Где находятся их центры?
Дайте определение четырехугольника.
Дайте определение параллелограмма
Сформулируйте признак и свойства параллелограмма. Запишите формулы вычисления его периметра и площади
Дайте определение прямоугольника
Сформулируйте свойства прямоугольника. Запишите формулы вычисления его периметра и площади
Дайте определение ромба.
Сформулируйте свойства ромба. Запишите формулы вычисления его периметра и площади
Дайте определение квадрата
Сформулируйте свойства квадрата. Запишите формулы вычисления его периметра и площади
Дайте определение многоугольника, правильного многоугольника.
Дайте определение вписанного в окружность многоугольника.
Дайте определение описанного около окружности многоугольника.
Запишите формулы вычисления радиусов вписанного в окружность и описанного около окружности правильного многоугольника
Сформулируйте свойства сторон и углов правильного многоугольника
Литература:
А.Д. Александров, Геометрия 10 кл., М.: Просвещение, 2014
Л.С. Атанасян, Геометрия 10-11, М.: Просвещение, 2014
Погорелов А.В. Геометрия: Учебник для 7-11классов средней школы.- Москва: Просвещение, 1993
ВСР 29. Решение задач на параллельность прямых и плоскостей в пространстве
Цель: Сформировать умения решать задачи на параллельность прямых и плоскостей в пространстве.
Методические рекомендации:
При выполнении работы необходимо знать признаки параллельности прямых, прямой и плоскости, теоремы о параллельных прямых и о параллельных плоскостях
Выполнить письменное задание:
Вариант 1
Каково взаимное расположение прямых АВ1 и ВD1 в прямоугольном параллелепипеде АВСDA1B1C1D1?
Каково взаимное расположение прямой A1С1 и плоскости ВDA в кубе АВСDA1B1C1D1?
Даны три параллельные плоскости. Расстояние между 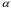 и и 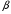 равно 3, а между равно 3, а между 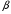 и и 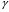 равно 5. Чему равно расстояние между равно 5. Чему равно расстояние между 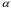 и и 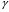 ? ?
Из точки А, не лежащей в параллельных плоскостях α и β, проведены две прямые, пересекающие α и β в точках В1 и В2, С1 и С2 соответственно. Найти длину В1В2, если С1С2 = 15м, АВ2 : В2С2 = 1 : 2.
Конец В отрезка АВ лежит в плоскости α. Точка С делит АВ в отношении АС:СD=3:4. Отрезок СD || α и равен 12см. Прямая АD пересекает α в точке Е. Найти длину ВЕ.
Вариант 2
ABCDA1B1C1D1 – куб. Каково взаимное расположение прямых В1В и А1С?
Каково взаимное расположение прямой ВС1 и плоскости A1B1D1 в прямоугольном параллелепипеде АВСDA1B1C1D1?
Даны три параллельные плоскости. Расстояние между 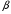 и и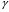 равно 7см, а между равно 7см, а между 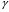 и и 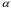 равно 9см. Чему равно расстояние между равно 9см. Чему равно расстояние между 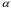 и и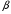 ? ?
Из точки М, не принадлежащей 2 параллельным плоскостям, проведены 2 прямые, пересекающие эти плоскости в точках А1 и А2; В1 и В2 соответственно, причем МА1=4см, В1В2=9см, А1А2=МВ1. Найти МА2 и МВ2.
Через конец А отрезка АВ проведена плоскость. Через конец В и т.С этого отрезка проведены параллельные прямые, пересекающие плоскость в т.В1 и С1. Найти длину ВВ1, если: СС1 = 15 см и АС : ВС = 2 : 3
Вариант 3
ABCDA1B1C1D1 – куб. Каково взаимное расположение прямых D1D и АС?
Каково взаимное расположение прямой D1A и плоскости ВCB1 в прямоугольном параллелепипеде АВСDA1B1C1D1?
Даны три параллельные плоскости. Расстояние между 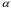 и и 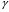 равно 13м, а между равно 13м, а между 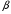 и и 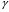 равно 6м. Чему равно расстояние между равно 6м. Чему равно расстояние между 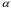 и и 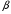 ? ?
Из точки D, не лежащей в параллельных плоскостях α и β, проведены 2 луча, пересекающие α и β в точках А1 и В1; А2 и В2 соответственно. Найти длину А 2В2, если А2D : А1 А2 = 7 : 2, А1 В1 = 15м.
Через конец А отрезка АВ проведена плоскость. Через конец В и т.С этого отрезка проведены параллельные прямые, пересекающие плоскость в т.В1 и С1. Найти длину ВВ1, если СС1 = 8,1 см и АВ : АС = 11 : 9
Вариант 4
Каково взаимное расположение прямых BD1 и A1C1 в прямоугольном параллелепипеде АВСDA1B1C1D1?
Каково взаимное расположение прямой ВС и плоскости ВDA в кубе АВСDA1B1C1D1?
Даны три параллельные плоскости. Расстояние между 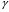 и и 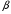 равно 4, а между равно 4, а между 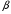 и и 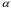 равно 2. Чему равно расстояние между равно 2. Чему равно расстояние между 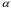 и и 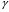 ? ?
Плоскость, параллельная прямой АВ треугольника АВС, пересекает сторону АС в точке А1, сторону ВС – в точке В1. Найти длину А1В1, если АВ=25см, А1А:А1С= 2:3
Через конец А отрезка АВ проведена плоскость. Через конец В и т.С этого отрезка проведены параллельные прямые, пересекающие плоскость в т.В1 и С1. Найти длину ВВ1, если АВ=6см, АС:СС1= 2:5
ВСР 30. Геометрические преобразования пространства
Цель: Иметь представление о геометрических преобразованиях пространства
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы, выполнить рисунки с обозначениями:
Дайте определение движения
Сформулируйте общие свойства движений
Дайте определение центральной симметрии
Дайте определение осевой симметрии
Дайте определение зеркальной симметрии
Дайте определение параллельного переноса
Дайте определение поворота
Дайте определение преобразования подобия
Приведите примеры, рис.
Выполнить письменное задание:
Вариант 1.
Какая из данных точек симметрична относительно начала координат точке A(2;-1;6)
а) (-2;-1;6); б) (2;1;6); в) (-2;1;-6)?
Какая из данных точек симметрична относительно оси Oy точкеA(3;-6;8)
а) (-3;6;-8); б) (-3;-6;-8); в) (3;6;8)?
Какая из данных фигур имеет центр симметрии:
а) шар; б) конус; в) куб?
Какие координаты имеет точка, симметричная точкеA(2;-1;6) относительно плоскости xy
а) (-2;1;-6); б) (2;-1;-6); в) (2;1;6)?
Какие координаты имеет точка, симметричная точке M(2;-1;5) относительно плоскости xz
а) (-2;1;-5); б) (2;1;5); в) (-2;-1;-5)?
Какая из данных фигур имеет только одну плоскость симметрии:
а) равнобедренный треугольник; б) параллелограмм; в) прямоугольник;
г) равнобокая трапеция?
Сколько плоскостей симметрии имеет прямоугольный параллелепипед
а) 3; б) 5; в) 9?
Имеет ли тело вращения плоскость симметрии:
а) да; б) нет; в) не всякое?
Сколько центров симметрии имеет правильная треугольная призма:
а) 1; б) 3; в) не имеет?
Сколько центров симметрии имеет отрезок:
а)1; б) бесконечно много; в) не имеет?
Сколько осей симметрии имеет правильный треугольник:
а) 1; б) 3; в) не имеет?
Сколько плоскостей симметрии имеет правильная четырехугольная призма:
а) 5; б) 3; в)1?
Вариант 2.
Какая из данных точек симметрична относительно начала координат точке B(-3;1;5)
а) (-3;1;-5); б) (3;-1;-5); в) (-3;-1;-5)?
Какая из данных точек симметрична относительно оси Oy точкеB(-1;5;-4)
а) (1;5;4); б) (-1;-5;-4); в) (1;-5;4)?
Какая из данных фигур имеет ось симметрии:
а) цилиндр; б) шар; в) наклонная призма?
Какие координаты имеет точка, симметричная точкеA(2;-1;6) относительно плоскости xz
а) (-2;1;-6); б) (2;1;-6); в) (2;-1;-6)?
Какие координаты имеет точка, симметричная точке A(2;-1;6) относительно плоскости yz
а) (-2;-1;6); б) (2;1;6); в) (2;-1;-6)?
Где находится центр симметрии прямоугольного параллелепипеда:
а) в точке пересечения диагоналей; б) в вершине; в) вне параллелепипеда?
Сколько плоскостей симметрии имеет прямоугольный параллелепипед, у которого два линейных размера равны:
а) 5; б) 7; в) 3?
Сколько центров симметрии имеет параллелепипед:
а) 1; б) 3; в) не имеет?
Сколько центров симметрии имеет двугранный угол:
а) 1; б) 3; в) не имеет?
Сколько осей симметрии имеет отрезок:
а)1; б) бесконечно много; в) не имеет?
Сколько плоскостей симметрии имеет правильная четырехугольная пирамида:
а) 4; б) 3; в) 1?
Сколько плоскостей симметрии имеет треугольная пирамида:
а) 3; б) 6; в) 1?
Литература:
1. А.Д. Александров, Геометрия 11 кл., М.: Просвещение, 2014, гл. IX
2. Л.С. Атанасян, Геометрия 10-11, М.: Просвещение, 2014, гл. V,  3 3
3. Погорелов А.В. Геометрия: Учебник для 7-11классов средней школы.- Москва: Просвещение, 1993,  18 18
Раздел 9. Многогранники
ВСР 31. Изготовление моделей правильных многогранников
Цель: Развитие интереса к предмету. Закрепить понятия правильных многогранников и их элементов при изготовлении моделей
Методические рекомендации:
Изготовить модель правильного многогранника, используя развертки, изображенные на стр. 80 в учебнике Л.С. Атанасяна, Геометрия 10-11, М.: Просвещение, 2014
ВСР 32. Изготовление моделей призмы
Цель: Развитие интереса к предмету. Закрепить понятие призмы и ее элементов при изготовлении модели
Методические рекомендации:
Изготовить модель призмы, используя инструкции и развертки, изображенные на страницах:
http://constryctor.ru/specialnoe-risovanie/postroenie-razvertki-prizmy/
http://mash-xxl.info/info/232540/
https://yandex.ru/images/search?text=развертка%20призмы&stype=image&lr=11464&noreask=1&source=wiz
ВСР 33. Изготовление моделей пирамиды
Цель: Развитие интереса к предмету. Закрепить понятие пирамиды и ее элементов при изготовлении модели
Методические рекомендации:
Изготовить модель пирамиды, используя инструкции и развертки, изображенные на страницах:
http://fb.ru/article/143219/piramida---razvertka-razvertka-piramidyi-dlya-skleivaniya-razvertki-iz-bumagi#image418641
http://www.trivida.ru/chertezhi_view_post.php?id=29
https://yandex.ru/images/search?text=развертка%20пирамиды&stype=image&lr=11464&noreask=1&source=wiz
ВСР 34. Симметрии в кубе, в параллелепипеде, в призме и пирамиде.
Цель: иметь представление о симметрии в кубе, в параллелепипеде, в призме и пирамиде
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы, выполнить рисунки с обозначениями:
Дайте определения точек, симметричных относительно точки, прямой, плоскости
Дайте определения центра, оси, плоскости симметрии
Ск. центров (осей, плоскостей) симметрии может иметь фигура?
Приведите примеры симметрии в природе, архитектуре, технике, быту (можно с рис.)
Что наз. элементами симметрии многогранника?
Перечислите элементами симметрии правильных многогранников,параллелепипеда, призмы, пирамиды
Выполнить письменное задание:
Вариант 1.
Сколько плоскостей симметрии имеет прямоугольный параллелепипед, у которого два линейных размера равны:
а) 5; б) 7; в) 3?
Сколько центров симметрии имеет параллелепипед:
а) 1; б) 3; в) не имеет?
Сколько центров симметрии имеет двугранный угол:
а) 1; б) 3; в) не имеет?
Сколько осей симметрии имеет отрезок:
а)1; б) бесконечно много; в) не имеет?
Сколько плоскостей симметрии имеет правильная четырехугольная пирамида:
а) 4; б) 3; в) 1?
Сколько плоскостей симметрии имеет треугольная пирамида:
а) 3; б) 6; в) 1?
Вариант 2.
Сколько плоскостей симметрии имеет прямоугольный параллелепипед
а) 3; б) 5; в) 9?
Имеет ли тело вращения плоскость симметрии:
а) да; б) нет; в) не всякое?
Сколько центров симметрии имеет правильная треугольная призма:
а) 1; б) 3; в) не имеет?
Сколько центров симметрии имеет отрезок:
а)1; б) бесконечно много; в) не имеет?
Сколько осей симметрии имеет правильный треугольник:
а) 1; б) 3; в) не имеет?
Сколько плоскостей симметрии имеет правильная четырехугольная призма:
а) 5; б) 3; в)1?
Литература:
1. А.Д. Александров, Геометрия 11 кл., М.: Просвещение, 2014, гл.V, §§ 22, 23, 26
2. Л.С. Атанасян, Геометрия 10-11, М.: Просвещение, 2014, гл. III, 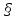 3 3
3. Погорелов А.В. Геометрия: Учебник для 7-11классов средней школы.- Москва: Просвещение, 1993,  18 18
ВСР 35. Построение сечений многогранников
Цель: Формировать умения строить сечения многогранников методом следов
Методические рекомендации:
Сечением называется пересечение фигуры с данной плоскостью.
Существует три основных метода построения сечений многогранников: метод следов, метод вспомогательных сечений, комбинированный метод.
Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения следа секущей плоскости на плоскости основания многогранника.
В основе построения сечения методом следов лежат две теоремы:
1. если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости;
2. если плоскость проходит через прямую, параллельную другой плоскости, и эти плоскости пересекаются, то линия их пересечения параллельна первой прямой.
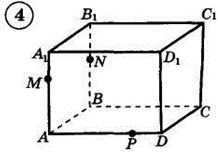
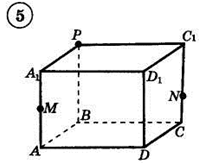
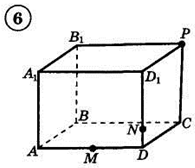
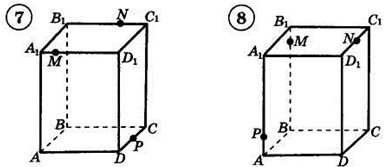
Например: Построить сечение (PQR) параллелепипеда.
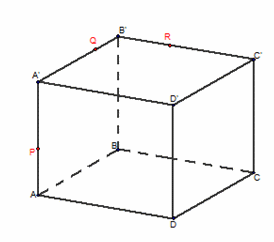 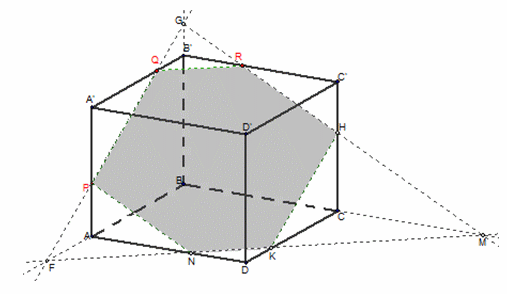
Построение:
1) Строим PQ и QR;2) PQ ∩ BA = F, PQ ∩ BB' = G;3) GR ∩ CC' = H, GR ∩ BC = M;4) FM ∩ AD = N, FM ∩ DC = K;5) PQRHKN — искомое сечение.
Выполнить письменное задание:
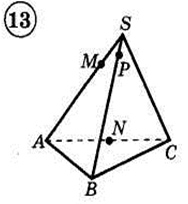
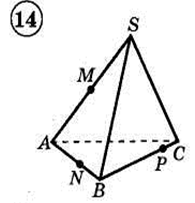
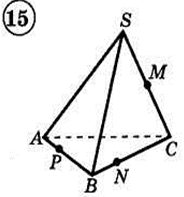
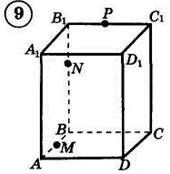
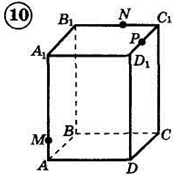
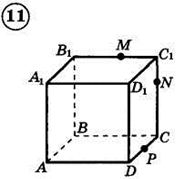
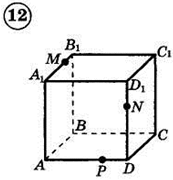
1. Построить сечение треугольной пирамиды плоскостью, проходя�щей через три указанные точки(увеличить рис.):
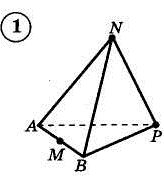 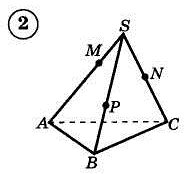 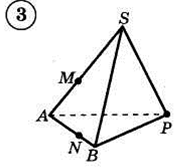 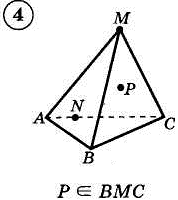 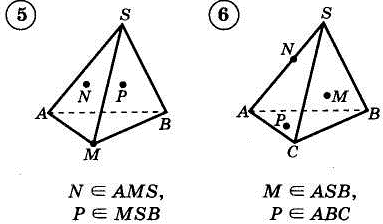
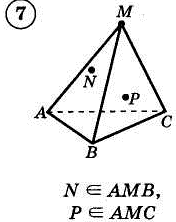 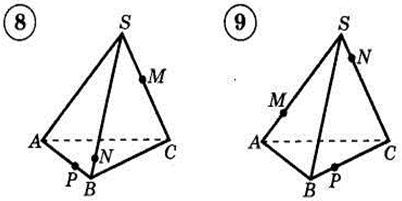 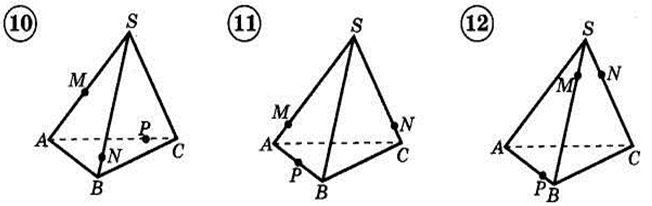   
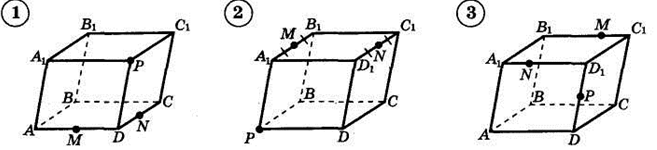
2. Построить сечение параллелепипеда плоскостью, проходя�щей через три указанные точки(увеличить рис.):
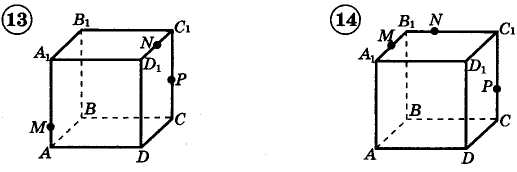
Раздел 10. Тела и поверхности вращения
ВСР 36. Изготовление моделей цилиндра и конуса
Цель: Развитие интереса к предмету. Закрепить понятия тел вращения и их элементов при изготовлении моделей
Методические рекомендации:
Изготовить модели цилиндра и конуса, используя инструкции и развертки, изображенные на страницах:
http://tepka.ru/Cherchenie_7-8/15.html
http://www.kakprosto.ru/kak-66910-kak-nachertit-razvertku-konusa
https://yandex.ru/images/search?text=развёртка%20конуса&stype=image&lr=11464&noreask=1&source=wiz
http://tvlad.ru/geometriya/vkroyka-dlya-konusa.html
https://yandex.ru/images/search?text=развёртка%20цилиндра&stype=image&lr=11464&noreask=1&source=wiz
ВСР 37. Шар и сфера, их сечения. Касательная плоскость к сфере.
Цель: Иметь представление о шаре и сфере, их сечениях, касательной плоскости к сфере, уметь применять полученные знания к решению задач
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы, выполнить рисунки с обозначениями:
Дайте определения сферы, шара, выполните рис.
Дайте определения центра, радиуса, диаметра сферы, шара, выполните рис.
Какие точки шара наз. диаметрально противоположными?
Сформулируйте теорему о сечении шара плоскостью, выполните рис.[3]
Сформулируйте теорему о пересечении шара и сферы с плоскостью, выполните рис.[1]
Дайте определение диаметральной плоскости шара
Дайте определения большого круга и большой окружности
Дайте определения касательная плоскости к сфере и точки касания
Сформулируйте теорему о касании сферы и плоскости
Выполнить письменное задание: № 580, 592[2]
Литература:
1. А.Д. Александров, Геометрия 10 кл., М.: Просвещение, 2014, гл. IV, § 15
2. Л.С. Атанасян, Геометрия 10-11, М.: Просвещение, 2014, гл. VI,  3 3
3. Погорелов А.В. Геометрия: Учебник для 7-11классов средней школы.- Москва: Просвещение, 1993,  20 20
ВСР 38. Решение задач на нахождение элементов тел вращения
Цель: Формировать умения находить элементы тел вращения.
Методические рекомендации:
|
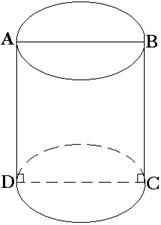
Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Прямой круговой цилиндр как тело вращения получается при вращении прямоугольника вокруг одной из его сторон.
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
|
|
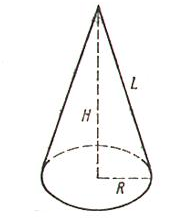
Конусом называется тело, которое состоит из круга – основание конуса; точки, не лежащей в плоскости этого круга – вершины конуса, и всех отрезков, соединяющих вершину конуса с точками основания.
Конус называется прямым, если прямая соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
Прямой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.
Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением.
|
Решить задачи:
Высота конуса 6 см, а образующая 10см. Найти радиус основания конуса, площадь осевого сечения и площадь боковой поверхности.
Высота цилиндра 8 см, а диагональ его осевого сечения образует с плоскостью основания угол 30 . Найти радиус цилиндра, площадь осевого сечения и площадь боковой поверхности. . Найти радиус цилиндра, площадь осевого сечения и площадь боковой поверхности.
Радиус шара 17см. Найти площадь сечения шара, проведенного на расстоянии 15см от центра шара.
Высота цилиндра 8дм, радиус основания 5дм. В цилиндре проведено сечение, параллельное его оси так, что получился квадрат. Найти расстояние от этого сечения до оси цилиндра.
Раздел 11. Измерения в геометрии
ВСР 39. Объем и его измерение. Интегральная формула объема
Цель:Иметь представление об объеме тела, знать интегральную формулу объема, уметь применять ее при решении задач.
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы:
Дать определение простого тела [3]
Дать определение объема [3]
Записать общую формулу для объемов тел вращения
Вывести формулу для нахождения объема шара
Выполнить письменное задание № 647, 674[1]
|
 Скачать 1.69 Mb.
Скачать 1.69 Mb. 3
3 18
18 3
3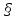 18
18





















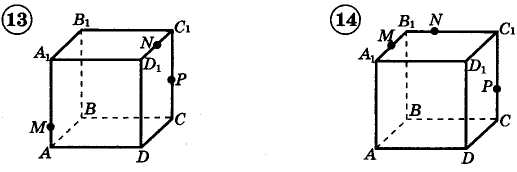
 3
3 20
20
 .
.  .
.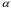 и
и 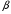 равно 3, а между
равно 3, а между 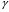 равно 5. Чему равно расстояние между
равно 5. Чему равно расстояние между 



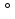 .
.