Литература:
Никольский С.М., Алгебра и начала математического анализа,11 класс, М.: Просвещение, 2014
Яковлев Г.Н. Математика для техникумов. Алгебра и начала анализа ч.1. Москва «Наука»
Интернет-ресурсы http://uztest.ru/abstracts/?idabstract=183948
ВСР 10. Обратные функции. График обратной функции. Арифметические операции над функциями. Сложная функция.
Цель: Знатьопределениеобратной функции, сложной функции, графика обратной функции, арифметические операции над функциями.
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы:
Дать определение обратной функции
Перечислить основные элементарные функции
Дать определение сложной функции
Дать определение графика обратной функции
Знать арифметические операции над функциями
Литература:
Никольский С.М., Алгебра и начала математического анализа,11 класс, М.: Просвещение, 2014,§§1,3
Яковлев Г.Н. Математика для техникумов. Алгебра и начала анализа ч.1. Москва «Наука» ,§16
М.Я. Пратусевич, Алгебра и начала математического анализа, 10 класс, М.: Просвещение, 2014,§23
Интернет-ресурсы http://df-dt.com/%D0%BE%D0%BF%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D0%B8-%D0%BD%D0%B0%D0%B4-%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F%D0%BC%D0%B8.html
ВСР 11. Преобразование графиков функций.
Цель: Знатьосновные способы преобразования графиков функций.
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы:
В чем заключается способ симметрии относительно осей координат?
В чем заключается способ сдвига вдоль осей координат?
В чем заключается способ растяжения и сжатия вдоль осей координат?
В чем заключается способ построения графика функции 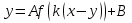 по графику функции по графику функции 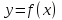 ? ?
В чем заключается способ симметрии относительно прямой 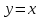 ? ?
Разобрать примеры № 1-3, записать решение
Литература:
Никольский С.М., Алгебра и начала математического анализа,11 класс, М.: Просвещение, 2014,§§1(6)
ВСР 12. «Радианная мера угла. Тригонометрические функции произвольного аргумента. Основные тригонометрические тождества».
Цель: На основе известных сведений о длине дуги окружности рассмотреть определение радианной меры угла, изучить правила перевода радианной меры в градусную и обратно, нахождения значения тригонометрических функций по известному значению одной из них, применения основных тригонометрических формул к преобразованию выражений и доказательству тождеств.
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы:
Дать определение единичной окружности
Дать определение радианной меры дуги окружности
Записать формулы перехода от радианной меры угла к градусной и наоборот
Разобрать примеры № 1,2, записать решение [2]
Как построено соответствие между действительными числами и точками единичной окружности (рис.65)? [2]
Дать определение синуса, косинуса, тангенса и котангенса произвольного аргумента (действительного числа)
Записать основные тригонометрические тождества
Разобрать примеры № 1-3, записать решение [2]
Перерисовать рис.71 (знаки тригонометрических функций) [2]
Разобрать пример № 1, записать решение [2]
Перерисовать таблицу со стр.234 [2]
Разобрать примеры № 2-6, записать решение [2]
II. Выполнить письменное задание № 5.40, 5.42 [2]
Литература:
Никольский С.М., Алгебра и начала математического анализа,10 класс, М.: Просвещение, 2014,§§7,8
Яковлев Г.Н. Математика для техникумов. Алгебра и начала анализа ч.1. Москва «Наука» ,§24
ВСР 13. «Тригонометрические функции, их свойства».
Цель: Знать свойства тригонометрических функций, с понятия знаков, периодичности, четности и нечетности тригонометрических функций; уметь
определять знаки выражения тригонометрических функций используя свойства тригонометрических функций.
Методические рекомендации:
Выполнить письменное задание:
Вариант 1
1. Найдите значение:
а) sin (–765°); б) tg .
2. Определите знак выражения
sin a × cos a × tg a × сtg a:
а) a = 160°; б) a = – .
3. Оцените выражение:
6 – 4sin x.
|
Вариант 2
1. Найдите значение:
а) cos 1050°; б) 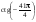 . .
2. Определите знак выражения
sin a × cos a × tg a × сtg a:
а) a = –240°; б) a = 2,2.
3. Оцените выражение:
3cos x + 1.
|
Вариант 3
1. Найдите значение:
а) tg ; б) cos (–1755°).
2. Определите знак выражения
sin a × cos a × tg a × сtg a:
а) a = –70°; б) a = .
3. Оцените выражение:
7sin2 x – 5.
|
Вариант 4
1. Найдите значение:
а) 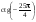 ; б) sin 1410°. ; б) sin 1410°.
2. Определите знак выражения
sin a × cos a × tg a × сtg a:
а) a = 198°; б) a = – 6,4.
3. Оцените выражение:
2cos x – 4.
|
Вариант 5
1. Найдите значение:
а) cos 1500°; б) 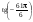 . .
2. Определите знак выражения
sin a × cos a × tg a × сtg a:
а) a = 256°; б) a = – .
3. Оцените выражение:
1 – 2sin2 x.
|
Вариант 6
1. Найдите значение:
а) 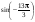 ; б) сtg 1125°. ; б) сtg 1125°.
2. Определите знак выражения
sin a × cos a × tg a × сtg a:
а) a = – 170°; б) a = 6,1.
3. Оцените выражение:
2 + 5cos x.
|
ВСР 14. «Формулы сложения».
Цель: Знать формулы сложения тригонометрических функций, формулы приведения и двойных аргументов, основные тригонометрические тождества, уметь применять их для преобразований тригонометрических выражений.
Методические рекомендации:
При выполнении работы необходимо использовать основные тригонометрические тождества, формулы сложения тригонометрических функций, формулы приведения и двойных аргументов:
Основные тригонометрические тождества:
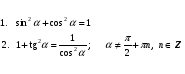 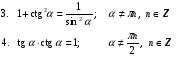
Формулы сложения:
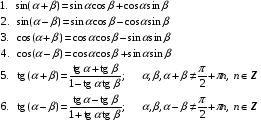
Формулы двойного и половинного аргументов:
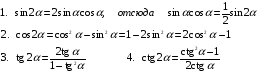
Например:
Найти cos a, tg a, сtg a, если известно, что
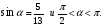
Решение: заметим, что 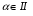 четверти и четверти и 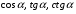 - отрицательны. - отрицательны.
Из формулы 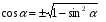 имеем: имеем:
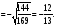 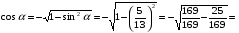
Из формулы 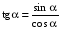 : : 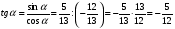 . .
Из формулы 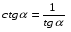 : : 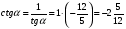 . .
Ответ: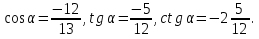
Заметим, что если известно значение 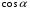 , то вычисления аналогичны. , то вычисления аналогичны.
Упростите выражения:
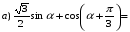 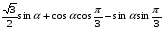 = =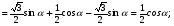
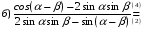 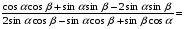
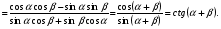
3. Известно, что 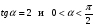 . Вычислите . Вычислите . .
Решение:  четверти, значит четверти, значит 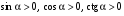 . .
Из формулы 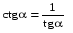 : : 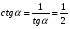 . .
Из формулы 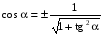 : : 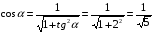 . .
Из формулы 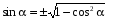 : :
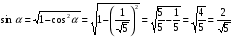
Ответ: 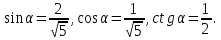
Выполнить письменное задание: №1 нужно найти значения выражения,
в №3 нужно найти значения sin2α, cos2α и tg2α, а все выражения упрощать до получения одночлена
Вариант 1
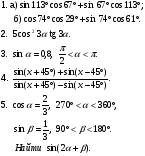
|
Вариант 2
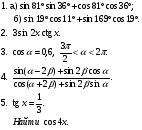
|
Вариант 3
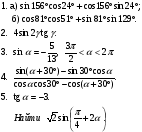
|
Вариант 4
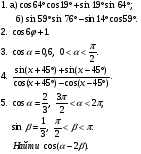
|
ВСР 15. «Решение тригонометрических уравнений».
Цель:Знать методы решения тригонометрических уравнений, уметь применять их при решении уравнений.
Методические рекомендации:
Уравнение
|
Формулы решения
|
Частные случаи
|
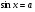
|
при 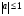 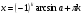 , , 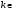 Z Z
при 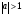 - решений нет - решений нет
|
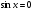 ; ; 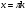 , , 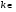 Z Z
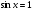 ; ; 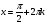 , , 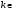 Z Z
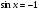 , , 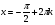 , ,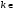 Z Z
|
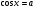
|
при 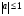 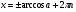 , , 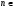 Z Z
при 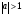 - решений нет - решений нет
|
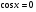 ; ; 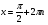 , , 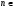 Z Z
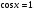 ; ; 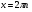 , , 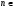 Z Z
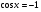 ; ; 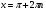 , , 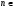 Z Z
|
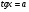
|
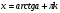 , , 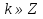
|
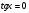 ; ; 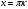 , ,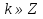
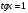 ; ; 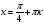 , ,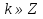
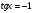 ; ;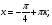 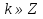
|
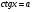
|
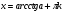 , , 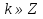
|
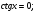 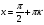 , ,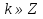
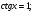 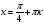 , ,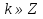
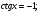 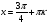 , ,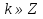
|
|
|
|
Основные методы решения
Любое тригонометрическое уравнение в процессе решения с помощью надлежащих преобразований должно быть приведено к простейшим. Наиболее часто при решении тригонометрических уравнений применяются следующие методы:
разложение на множители;
способ замены (сведение к алгебраическим уравнениям);
сведение к уравнениям, однородным относительно и ;
преобразование суммы тригонометрических функций в произведение;
преобразование произведения тригонометрических функций в сумму;
использование формул понижения степени;
равенство одноименных тригонометрических функций;
равенство одноименных тригонометрических функций
введение вспомогательного аргумента.
При этом, как правило, в процессе решения тригонометрического уравнения приходится использовать не один, а несколько из указанных выше методов.
Например: Решите уравнение:
1) 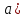 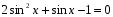
Замена 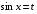 , ,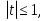
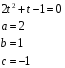 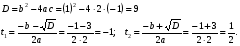
Вернемся к замене:
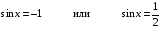
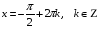 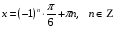
Ответ: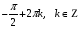 ; ; 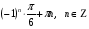 . .
В некоторых уравнениях требуется сделать дополнительное преобразование, чтобы уравнение свелось к квадратному:
b)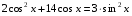
Заменим, используя формулу (1) п. 6, 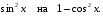
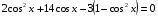
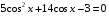
Замена: 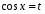 , , 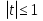
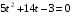
Решив уравнение, найдем 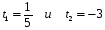
Обратная замена:
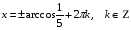 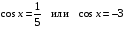 - посторонний корень, - посторонний корень,
Ответ: 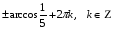 . .
2) 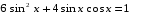
Если в однородном уравнении второй степени присутствует свободный член  , то его можно заменить: , то его можно заменить: 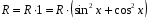 . .
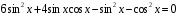
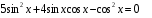 , ,
откуда 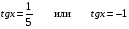 , ,
т.е. 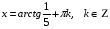 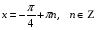
Ответ: 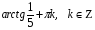 ; ; 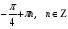 . .
3) 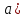 
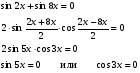
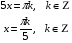 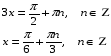
Ответ: 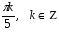 ; ; 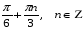 . .
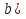 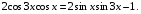
Преобразуем выражение и воспользуемся формулой (3) п. 16.
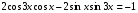
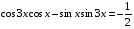
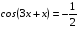
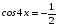 — простейшее тригонометрическое уравнение — простейшее тригонометрическое уравнение
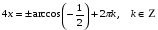
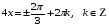
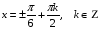
Ответ: 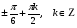
Выполнить письменное задание:
ВАРИАНТ 1
Решите тригонометрические уравнения:
2sin2 x – 5sin x – 7 = 0
12sin2 x + 20cos x – 19 = 0
3sin2 x + 14sin x cos x + 8cos2 x = 0
7 tg x – 10ctg x + 9 = 0
5sin 2x – 14cos2 x + 2 = 0
9cos 2x – 4cos2 x = 11sin 2x + 9
|
ВАРИАНТ 2
Решите тригонометрические уравнения:
10cos2 x – 17cos x + 6 = 0
2cos2 x + 5sin x + 5 = 0
6sin2 x + 13sin x cos x + 2cos2 x = 0
5 tg x – 4ctg x + 8 = 0
6cos2 x + 13sin 2x = –10
2sin2 x + 6sin 2x = 7(1 + cos 2x)
|
ВАРИАНТ 3
Решите тригонометрические уравнения:
1. 3sin2 x – 7sin x + 4 = 0
2. 6sin2 x – 11cos x – 10 = 0
3. sin2 x + 5sin x cos x + 6cos2 x = 0
4. 4 tg x – 12ctg x + 13 = 0
5. 5 – 8cos2 x = sin 2x
6. 7sin 2x + 9cos 2x = –7
|
ВАРИАНТ 4
Решите тригонометрические уравнения:
1. 10cos2 x + 17cos x + 6 = 0
2. 3cos2 x + 10sin x – 10 = 0
3. 2sin2 x + 9sin x cos x + 10cos2 x = 0
4. 3 tg x – 12ctg x + 5 = 0
5. 10sin2 x – 3sin 2x = 8
6. 11sin 2x – 6cos2 x + 8cos 2x = 8
|
ВАРИАНТ 5
Решите тригонометрические уравнения:
1. 10sin2 x + 11sin x – 8 = 0
2. 4sin2 x – 11cos x – 11 = 0
3. 4sin2 x + 9sin x cos x + 2cos2 x = 0
4. 3 tg x – 8ctg x + 10 = 0
5. 3sin 2x + 8sin2 x = 7
6. 10sin2 x + 11sin 2x + 6cos 2x = –6
|
ВАРИАНТ 6
Решите тригонометрические уравнения:
1. 3cos2 x – 10cos x + 7 = 0
2. 6cos2 x + 7sin x – 1 = 0
3. 3sin2 x + 10sin x cos x + 3cos2 x = 0
4. 6 tg x – 14ctg x + 5 = 0
5. 6sin2 x + 7sin 2x + 4 = 0
6. 7sin 2x – 9cos 2x =7
|
Раздел 6. Начала математического анализа
ВСР 16. Понятие о пределе последовательности. Предел функции на бесконечности и в точке.
Цель:Знать определение последовательности и способы ее задания. Иметь представление о пределе последовательности, пределе функции на бесконечности и в точке.
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы:
Дать определение последовательности[1]
Перечислить способы задания последовательности[1]
Перечислить свойства последовательностей[1]
Дать определение бесконечно малой и бесконечно большой величины
Сформулировать определение предела последовательности[1]
Сформулировать свойства пределов [2]
Сформулировать теорему Вейерштрасса
Сформулировать определение предела функции в точке[3]
Сформулировать теоремы о пределах[3]
II. Выполнить письменное задание № 4.35(а,ж,и)[2], 4.41(1,3,5) [3].
|
 Скачать 1.69 Mb.
Скачать 1.69 Mb.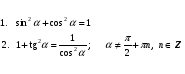
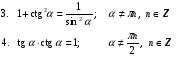
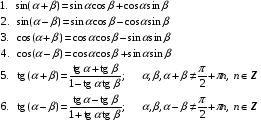
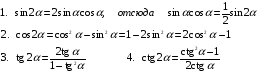
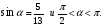
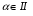 четверти и
четверти и 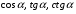 - отрицательны.
- отрицательны.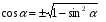 имеем:
имеем: 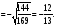
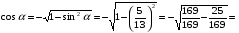
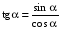 :
: 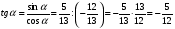 .
.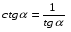 :
: 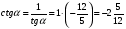 .
.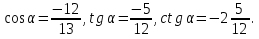
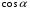 , то вычисления аналогичны.
, то вычисления аналогичны.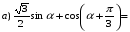
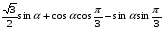 =
=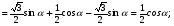
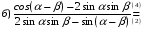
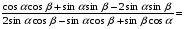
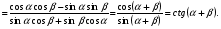
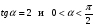 . Вычислите
. Вычислите .
.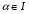 четверти, значит
четверти, значит 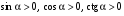 .
.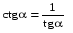 :
: 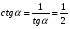 .
.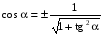 :
: 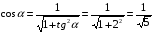 .
.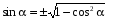 :
: 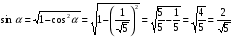
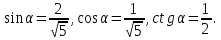
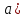
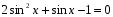
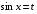 ,
,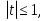
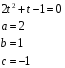
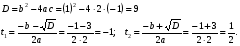
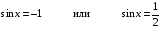
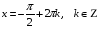
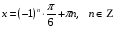
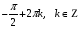 ;
; 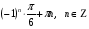 .
.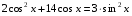
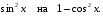
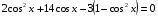
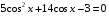
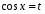 ,
, 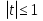
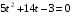
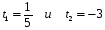
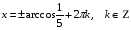
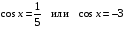 - посторонний корень,
- посторонний корень,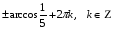 .
. 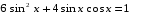
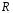 , то его можно заменить:
, то его можно заменить: 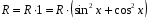 .
.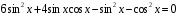
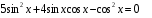 ,
,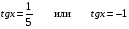 ,
,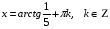
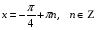
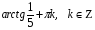 ;
; 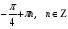 .
.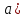

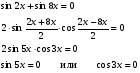
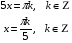
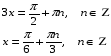
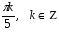 ;
; 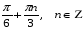 .
.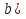
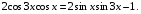
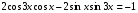
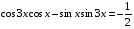
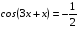
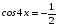 — простейшее тригонометрическое уравнение
— простейшее тригонометрическое уравнение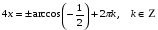
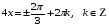
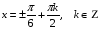
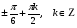

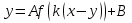 по графику функции
по графику функции 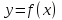 ?
?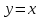 ?
?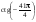 .
.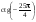 ; б) sin 1410°.
; б) sin 1410°.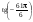 .
.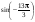 ; б) сtg 1125°.
; б) сtg 1125°.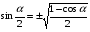
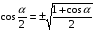
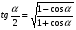
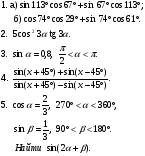
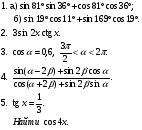
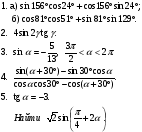
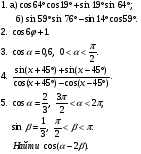
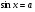
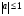
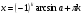 ,
, 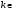 Z
Z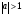 - решений нет
- решений нет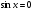 ;
; 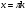 ,
, 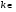 Z
Z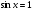 ;
; 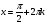 ,
, 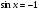 ,
, 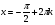 ,
,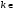 Z
Z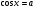
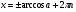 ,
, 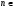 Z
Z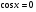 ;
; 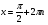 ,
, 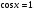 ;
; 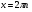 ,
, 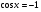 ;
; 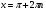 ,
, 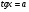
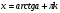 ,
, 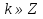
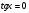 ;
; 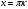 ,
,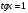 ;
; 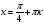 ,
,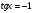 ;
;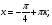
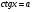
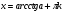 ,
, 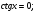
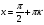 ,
,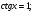
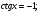
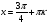 ,
,