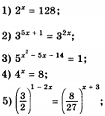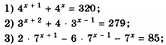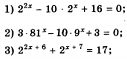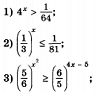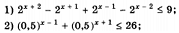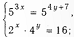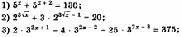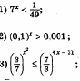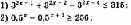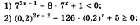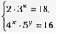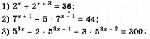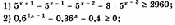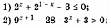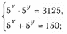|
|
ВСР математика. Методические рекомендации по выполнению внеаудиторной самостоятельной работы по дисциплине оуд. 04 Математика алгебра и начала математического анализа геометрия для студентов I курса
Литература:
http://lfostu.ucoz.ru/publ/sovremennye_podkhody_k_organizacii_uchebnogo_process/2_aprobacija_sovremennykh_podkhodov_k_organizacii_obrazovatelnogo_processa/formirovanie_professionalnykh_kompetencij_u_studentov_tekhnicheskikh_specialnostej_cherez_reshenie_matematicheskikh_zadach_prikladnogo_soderzhanija/36-1-0-335
http://videouroki.net/filecom.php?fileid=98663699
http://www.myshared.ru/slide/298605/
http://lib2.podelise.ru/docs/540/index-103486.html
http://rushkolnik.ru/docs/index-4488879.html
http://ppt4web.ru/matematika/podgotovka-k-egeh-po-matematike-reshenie-zadanijj-v.html
ВСР 5.« Равносильность неравенств и их систем.»
Цель: Знать виды неравенств и способы их решения, уметь выполнять равносильные преобразования неравенств и их систем.
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы:
Дать определение неравенства с одним неизвестным.
Разобрать примеры №1,2, записать решение
Какие неравенства наз. равносильными?
Записать теоремы о равносильности неравенств.
Дать определение линейного неравенства.
Разобрать примеры №1-3, записать решение
Дать определение квадратного неравенства.
Разобрать примеры №1-4, записать решение
Дать определение рационального неравенства
Разобрать примеры №1-4, записать решение
Дать определение системы неравенств.
Разобрать примеры № 1-5, записать решение
Выполнить письменное задание № 3.33(4), 3.34(6), 3.36(6), 3.37(4)
Литература:
Яковлев Г.Н. Математика для техникумов. Алгебра и начала анализа ч.1,2. Москва «Наука», 2000, § 14
ВСР 6.« Неравенства, содержащие знак абсолютной величины. Иррациональные неравенства».
Цель: Знать правила избавления от иррациональности, раскрытия модуля числа.
Разобрать принципы решения неравенств, содержащих знак абсолютной величины, иррациональных неравенств и уметь пользоваться ими при решении таких неравенств.
Методические рекомендации:
Изучить теоретический материал и письменно ответить на вопросы:
Записать определение модуля и его геометрическую интерпретацию.
Переписать содержимое таблицы на с.73[1]
Выписать следствие и решение неравенств из примера 85.
Записать вывод.
Разобрать пример №90
Выписать утверждения, помогающие избавиться от иррациональности на с.363[2] и замечания.
Разобрать примеры №84-86
Выписать более удачный способ решения примера 87
Выполнить письменное задание № I.178(в,г), I.181(в,г) [1], №XIII.70(б,в) [2]
Литература:
М.Я. Пратусевич, Алгебра и начала математического анализа, 10 класс, М.: Просвещение, 2014,§ 10
М.Я. Пратусевич, Алгебра и начала математического анализа. 11 класс, М.: Просвещение, 2014,§ 85
Раздел 3. Корни, степени и логарифмы
Рекомендации по самостоятельному изучению раздела
Понятие предела одно из наиболее важных и трудных в математическом анализе. Чтобы освоить технику вычисления пределов, студенту необходимо разобрать примеры, решённые в задачниках, обратить внимание, какие пределы вычисляются на основе двух «замечательных» пределов. Умение находить производные сложных функций необходимо для успешной сдачи экзамена и дальнейшего изучения высшей математики. Дифференциал функции имеет большое практическое применение.
Студент должен знать определение предела функции в точке и в бесконечности, определение производной, ее геометрический и механический смысл, правила и формулы дифференцирования функций, определение дифференциала функции; определение второй производной, ее физический смысл
Много вопросов математического и экономического анализа приводят к задачам, обратным задачам дифференциального исчисления. Поэтому при изучении данной темы студент должен приобрести навыки вычисления неопределенных интегралов, пользуясь таблицей и правилами интегрирования; методом подстановки, интегрирования по частям, вычислять определенные интегралы по формуле Ньютона-Лейбница.
ВСР 7. «Решение показательных уравнений, неравенств и их систем».
Цель: Знать методы решения показательных уравнений и неравенств, уметь применять их при решении таких уравнений
Методические рекомендации:
Степени чисел от 0 до 10
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
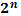
|
1
|
2
|
4
|
8
|
16
|
32
|
64
|
128
|
256
|
512
|
1024
|
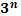
|
1
|
3
|
9
|
27
|
81
|
243
|
729
|
2187
|
6561
|
19683
|
59049
|
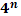
|
1
|
4
|
16
|
64
|
256
|
1024
|
4096
|
16384
|
65536
|
262144
|
|
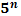
|
1
|
5
|
25
|
125
|
625
|
3125
|
15625
|
78125
|
390625
|
|
|
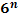
|
1
|
6
|
36
|
216
|
1296
|
7776
|
46656
|
279936
|
|
|
|
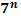
|
1
|
7
|
49
|
343
|
2401
|
16807
|
117649
|
|
|
|
|
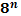
|
1
|
8
|
64
|
512
|
4096
|
32768
|
|
|
|
|
|
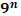
|
1
|
9
|
81
|
729
|
6561
|
59049
|
|
|
|
|
|
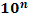
|
1
|
10
|
100
|
1000
|
10000
|
|
|
|
|
|
|
Свойства степеней
|
Свойства корней n-ой степени
|
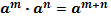 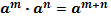
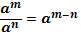 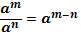
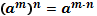 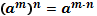
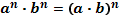 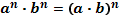
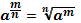 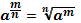
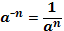 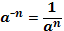
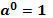 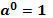
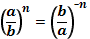 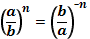
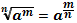
|
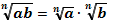 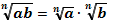
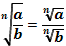 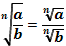
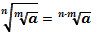 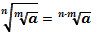
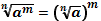 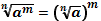
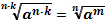 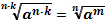
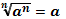 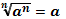
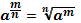 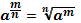
|
Выполнить письменное задание:
Решить уравнение:
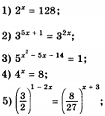
Решить уравнение:
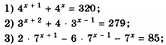
Решить уравнение:
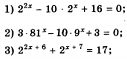
|
Решить неравенство:
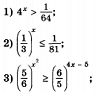
Решить неравенство:
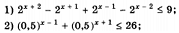
Решить неравенство:
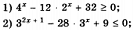
Решить систему:
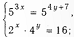
|
Вариант 1
Вариант 2
Решить уравнение:

Решить уравнение:
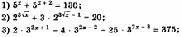
Решить уравнение:

|
Решить неравенство:
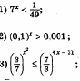
Решить неравенство:
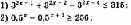
Решить неравенство:
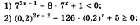
Решить систему:
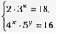
|
Вариант 3
Решить уравнение:

Решить уравнение:
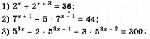
Решить уравнение:

|
Решить неравенство:

Решить неравенство:
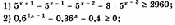
Решить неравенство:
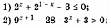
Решить систему:
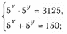
| |
|
|
 Скачать 1.69 Mb.
Скачать 1.69 Mb.