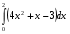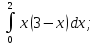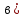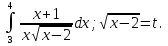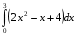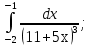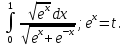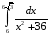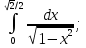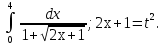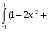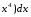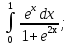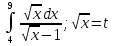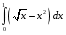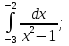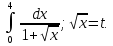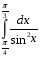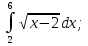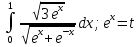ВСР математика. Методические рекомендации по выполнению внеаудиторной самостоятельной работы по дисциплине оуд. 04 Математика алгебра и начала математического анализа геометрия для студентов I курса
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
Составить уравнение касательнойВариант 1. Составить уравнение касательной к графику функции 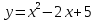 в точке с абсциссой в точке с абсциссой 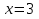 . .Вариант 2. Составить уравнение касательной к графику функции 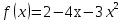 в точке с абсциссой в точке с абсциссой 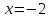 . .Вариант 3. Составить уравнение касательной к графику функции 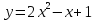 в точке с абсциссой в точке с абсциссой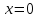 . .Вариант 4. Составить уравнение касательной к графику функции у = 3 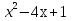 в точке с абсциссой в точке с абсциссой 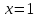 . .Вариант 5. Составить уравнение касательной к графику функции у = 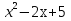 в точке с абсциссой в точке с абсциссой 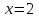 . .Вариант 6. Составить уравнение касательной к графику функции 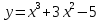 в точке с абсциссой в точке с абсциссой 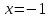 . .ВСР 18. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Цель: иметь представление о примерах использования производной для нахождения наилучшего решения в прикладных задачах, развитие интереса к предмету Методические рекомендации: Подготовить реферат по указанной теме. ВСР19. Применение производной к исследованию функций и построению графиков Цель: Уметь применять производную к исследованию функций и построению графиков Методические рекомендации:
II. Выполнить письменное задание № 7.25(3,4) Литература:
ВСР 20. Применение производной Цель: Уметь применять определение производной и ее физический (механический) смысл к решению прикладных задач. Методические рекомендации: Физический смысл производной заключается в том, что мгновенная скорость движения 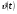 в момент времени t есть производная пути по времени, т.е. в момент времени t есть производная пути по времени, т.е. 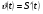 Физический смысл второй производной: ускорение прямолинейного движения в данный момент времени есть производная скорости по времени или вторая производная пути по времени. 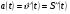
Вариант 1
Через какое время после начала движения угловая скорость ω вращения маховика будет равна 2?
Вариант 2
ВСР 21. Таблица интегралов Цель: Составить и выучить таблицу неопределенных интегралов Методические рекомендации: Таблица неопределенных интегралов( 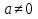 ) )
Литература:
ВСР 22. Вычисление неопределенного интеграла Цель: Отработать навыки вычисления неопределенных интегралов Методические рекомендации: Например: Вычислить интегралы: Решение 1) 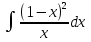 = =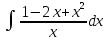 = =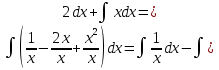 (получили сумму табличных интегралов )= (получили сумму табличных интегралов )= 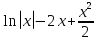 + c + c
Для вычисления этих интегралов пользовались основной таблицей интегралов, формулами тригонометрии, действиями со степенями и дробями.
имеем свойство дифференциала 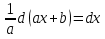 т.е. 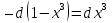 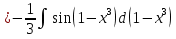 = = 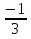 (-cos (1- (-cos (1-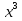 )) + c = )) + c = 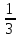 cos (1- cos (1-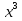 ) + c ) + c
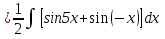 = =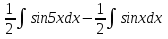 = =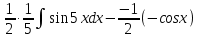 = = 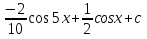 Таблица неопределенных интегралов 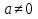 ∫ 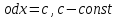 ∫ 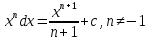 ∫ 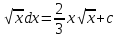 ∫ 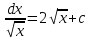 ∫ 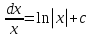 ∫ 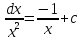 ∫ 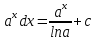 ∫ 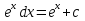 ∫ 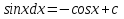 ∫ 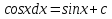 ∫ 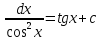 ∫ 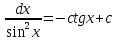 ∫ 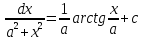 ∫ 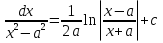 ∫ 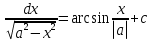 ∫ 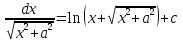 ∫ 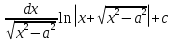
ВСР 23. Формула Ньютона—Лейбница Цель: Знать теорему Ньютона—Лейбница и разобрать применение ее к вычислению определенных интегралов Методические рекомендации:
II. Выполнить письменное задание № 6.46(1,2), 6.50 Литература:
ВСР 24. Вычисление определенного интеграла Цель: Отработать навыки вычисления определенных интегралов Методические рекомендации: Таблица неопределенных интегралов( 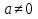 ) )∫ 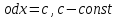 ∫ 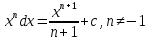 ∫ 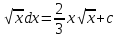 ∫ 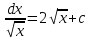 ∫ 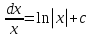 ∫ 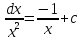 ∫ 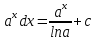 ∫ 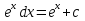 ∫ 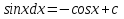 ∫ 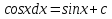 ∫ 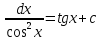 ∫ 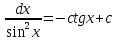 ∫ 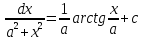 ∫ 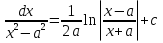 ∫ 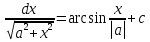 ∫ 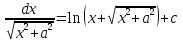 ∫ 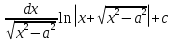 Например: Вычислить определенный интеграл. Нам понадобятся формула Ньютона-Лейбница 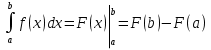 и правило замены переменной в определённом интеграле.
Вычислить определенные интегралы:
ВСР 25. Вычисление площадей плоских фигур Цель: Знать формулы для вычисления площадей плоских фигур Методические рекомендации:
II. Выполнить письменное задание № 6.52(а,б), 6.54(в) [1] Литература:
Раздел 7. Координаты и векторы ВСР 26. Векторы. Сложение векторов. Умножение вектора на число. Цель:Знать формулы для вычисления площадей плоских фигур Методические рекомендации: I. Изучить теоретический материал и письменно ответить на вопросы:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

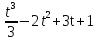 . В какие моменты времени t, ее скорость будет равна нулю?
. В какие моменты времени t, ее скорость будет равна нулю?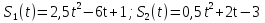 . В какой момент времени t0 скорости их будут равны?
. В какой момент времени t0 скорости их будут равны?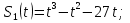
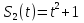 . Определить момент, когда скорости этих тел окажутся равными.
. Определить момент, когда скорости этих тел окажутся равными.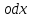
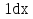
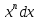
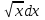
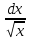
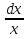
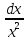
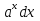
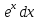
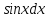
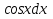
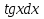
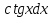
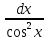
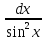
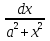
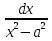
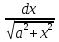
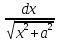
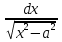
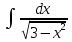
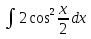
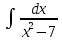
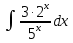
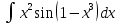
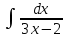
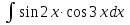
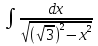 = arcsin
= arcsin 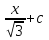
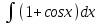 =
= 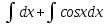 = x + sinx + c
= x + sinx + c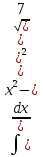 =
= 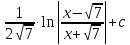
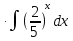 = 3
= 3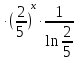
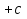
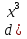 ) =
) = 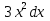 )
) 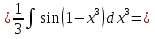
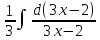 =
= 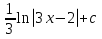
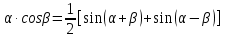 )=
)=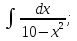
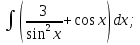
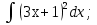
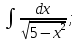
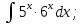
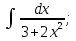
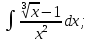
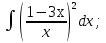
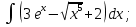
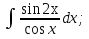
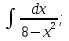
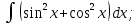
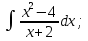
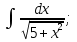
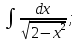
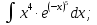
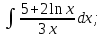
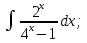
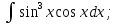
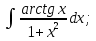
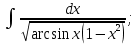
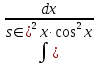
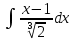
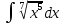
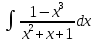
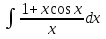
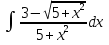
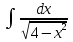
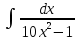
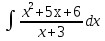
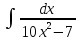
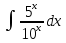
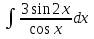
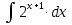
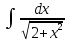
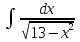
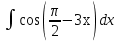
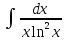
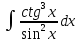
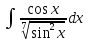
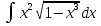
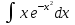
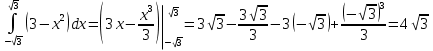
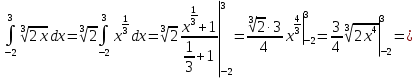
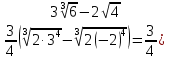 )
)