Прогнозирование принятия управленческих решений.. Методические указания по изучению курса 7 Варианты контрольной работы 9 Рекомендации по выполнению контрольной работы 12

• Название: Методические указания по изучению курса 7 Варианты контрольной работы 9 Рекомендации по выполнению контрольной работы 12
• Анкор: Прогнозирование принятия управленческих решений
• Дата: 10.12.2022
• Размер: 1.95 Mb.
• Имя файла: ppur.doc
• Тип: Методические указания; #837443
• страница: 4 из 12

5. Пример выполнения контрольной работы

Часть I

Выполнение заданий части I контрольной работы рассматривается на примере, имеющем исходную информацию, показанную в таблице 5

Таблица 5

Месяцы	1	2	3	4	5	6	7	8	9	10	11	12
Объем продаж (тыс. руб.)	32	48	53	46	68	75	56	77	98	69	85	92

1. Построить график изменения объемов продаж

График строится путем нанесения точек, соответствующих исходным данным, на координатное поле и соединения их прямыми отрезками.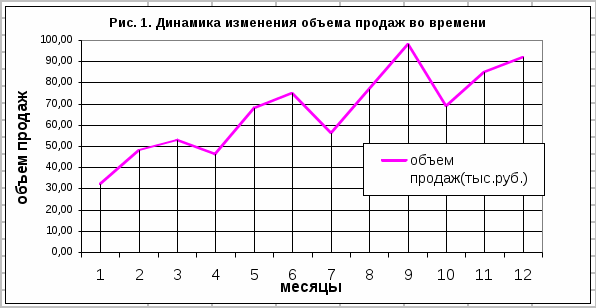


Рис. 1. График изменения объема продаж

2. Применить метод трёхчленной скользящей средней

Значения трехчленных скользящих средних вычисляются по формуле (1), а значения y_t-1, y_t , y_t+1 – выбираются из построенного графика рис. 1.

Полученные значения скользящих средних записываются в таблицу — (таблица 6)


Таблица 6

Месяцы	1	2	3	4	5	6	7	8	9	10	11	12
Объем продаж (тыс. руб.)	32	48	53	46	68	75	56	77	98	69	85	92
Скользящие средние		44,3	49,0	55,7	63,0	66,3	69,3	77,0	81,3	84,0	82,0

3. Построить систему нормальных уравнений и рассчитать константы прогнозирующей функции

Решим систему нормальных уравнений для логарифмической прогнозирующей функции =a+blnt.

Линеаризованное уравнение и система нормальных уравнений для этой функции даны в таблицах 3 и 4.

Линеаризованное уравнение — y_t= a + bt₁ ,

где t₁= lnt;

Система нормальных уравнений:

 y_t = an + b t₁

 y_t t₁ = a t₁ + b t₁²

Сомножитель n в первом уравнении системы характеризует объем выборочной совокупности (n= 12).

Определим все суммы, включенные в систему нормальных уравнений. Результаты вычислений удобно записать в специальную таблицу (таблицу 7).
Таблица 7

Месяцы	Объем продаж (yt)	ln t	yt lnt	(lnt)2	(прогноз.)
1	32	0,00	0,00	0,00	28,42
2	48	0,69	33,27	0,48	44,30
3	53	1,10	58,23	1,21	53,59
4	46	1,39	63,77	1,92	60,18
5	68	1,61	109,44	2,59	65,30
6	75	1,79	134,38	3,21	69,47
7	56	1,95	108,97	3,79	73,01
8	77	2,08	160,12	4,32	76,07
9	98	2,20	215,33	4,83	78,77
10	69	2,30	158,88	5,30	81,18
11	85	2,40	203,82	5,75	83,36
12	92	2,48	228,61	6,17	85,36
Всего: 78	799	19,99	1474,82	39,57	799,00

Таким образом:

 t₁ = lnt = 19,99; t₁² = 39,57; y_t= 799; y_tt₁ = 1474,82.

Подставим полученные результаты в систему

799 =12a +19,99b;

1474,82 = 19,99a + 39,57b.

Решив систему, найдем константы прогнозирующей функции:

a = 28,416; b= 22,915.

Следовательно, уравнение прогноза имеет вид:

= 28,416+22,915 lnt (12)

Зная параметры уравнения тренда, можно определить расчетные значения переменной для всех месяцев предпрогнозного периода. Так расчетная величина (t= 1) составляет:

y_t=1 = 28,416+22,915ln1 = 28,416 тыс.руб.

Как показывает анализ, исходные (y_t) и расчетные ( ) значения переменной соответствуют друг другу, что свидетельствует о правильности подбора прогнозирующей функции.
4. Определить наиболее вероятные объемы продаж в 13, 14 и 15 месяцы

После того как мы получили прогнозирующую функцию, можно прогнозировать развитие процесса в будущем. Для этого надо просто подставить в полученную формулу (12) значения t = 13, 14, 15.

Расчеты выполним по формулам:

y_t=13 = 28,416+22,915 ln13 = 87,192 тыс.руб.

y_t=14 = 28,416+22,915 ln14 = 88,890 тыс.руб.

y_t=15 = 28,416+22,915 ln15 = 90,471 тыс.руб.
5. Оценить правильность подбора прогнозирующей функции с помощью остаточной дисперсии, остаточного среднеквадратического отклонения и индекса корреляции

Рассчитаем правильность подбора прогнозирующей функции (в нашем случае – логарифмической кривой), сравнив её с другой прогнозной функцией ­— прямой линией. Линейная функция дана формулой (3), а система нормальных уравнений для неё — формула (4).

Для расчета статистических показателей воспользуемся формулами (5) – (8).

Искомые уравнения тренда:

Логарифмическая функция: = 28,416+22,915 lnt

Линейная функция: = 35,38+4,8t.

Вычислим значение средней арифметической y_ср:

y_ср = = 799 : 12= 66,58

Рассчитаем статистические показатели, для чего промежуточные данные вычислений (для суммарных значений) запишем в табличной форме:

Таблица 8

Месяцы	Объем продаж (yt)	Значения прогнозирующей функции		Значения ( yt– )2		( yt– yср)2
		Логарифми-ческойyt1	Линейной	Логарифми-ческойyt1	Линейной
1	32	28.42	40.18	12.85	66.91	1196
2	48	44.30	44.98	13.69	9.12	345
3	53	53.59	49.78	0.35	10.37	184
4	46	60.18	54.58	201.16	73.62	424
5	68	65.30	59.38	7.31	74.30	2
6	75	69.47	64.18	30.53	117.07	71
7	56	73.01	68.98	289.22	168.48	112
8	77	76.07	73.78	0.87	10.37	109
9	98	78.77	78.58	369.97	377.14	987
10	69	81.18	83.38	148.35	206.78	6
11	85	83.36	88.18	2.68	10.11	339
12	92	85.36	92.98	44.12	0.96	646
Всего	799		798.96	1121.10	1125.24	4421

Вычислим значения σ²_ост, σ_{ост ,} V:

Для логарифмической функции:

σ²_ост= = 1121,10 : 12 = 93,42;

σ_ост = = 9,67;

V= ( )* 100% = 9,67/66,58*100% = 14,52

Для линейной функции:

σ²_ост = 1125,24:12 =93,77;

σ_ост = = 9,68;

V= 9,68/66,58*100% =14,54

Сравнив эти три показателя между собой мы видим, что для логарифмической функции они меньше, чем для линейной. Следовательно, логарифмическая функция в нашем случае лучше подходит для уравнения прогноза.

Чтобы вычислить индекс корреляции R_y/t , необходимо вычислить общую дисперсию σ²_общ по формуле:

σ²_общ= = 4420,92 : 12 =368,41

Причем она одинакова для любой прогнозирующей функции (в нашем случае — для логарифмической и линейной).

Рассчитаем значение индекса корреляции R_y/t :

Для логарифмической функции:

Ry/t = 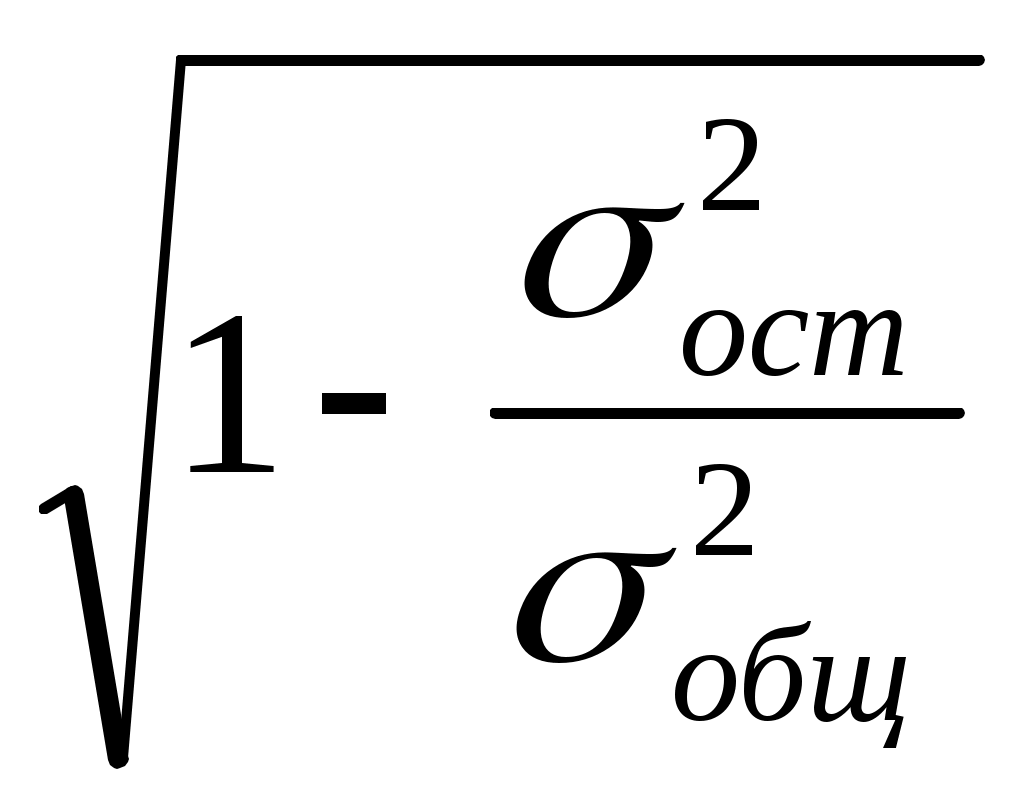= = 0,865

Для линейной функции:

Ry/t = = 0,862

Чем больше индекс корреляции, тем сильнее взаимодействие между переменными tи y_t .Как видно значение индекса корреляции приближается к 0,9, т.е. весьма высоко, что указывает на значительную тесноту связи между переменными. Однако для логарифмической функции оно всё же выше и по этому критерию она подходит больше, чем линейная.
6.Построить графики изменения объема продаж во времени, скользящей средней и прогнозирующей функции вида 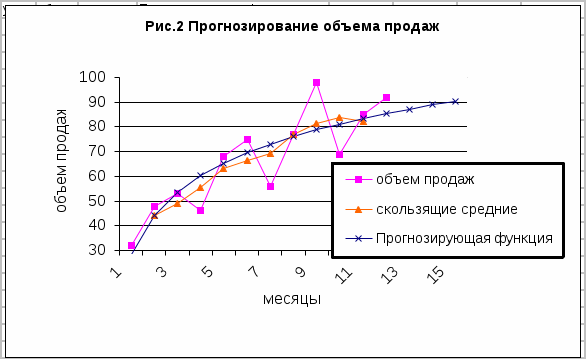=f(t)


ЧАСТЬ II

Выполнение заданий части II контрольной работы рассматривается на примере, имеющем исходную информацию, показанную в таблице 7.

Таблица 7

Месяцы	1	2	3	4	5	6	7	8	9	10	11	12
Объем продаж (тыс. руб.)	315	401	375	323	287	425	460	511	394	375	456	557
Месяцы	13	14	15	16	17	18	19	20	21	22	23	24
Объем продаж (тыс. руб.)	621	516	478	462	483	367	404	436	503	515	623	684

1.Построить графики исходной кривой, трехчленной скользящей средней, выбрать линию тренда, указать уравнение этой функции.

Для того, чтобы построить графики, используя программу Excel, необходимо войти в Excel, создать файл Контрольная работа, ввести столбец А – месяцы (1-24), ввести столбец B – объем продаж, в столбце С посчитать скользящие средние по формуле из части 1 данной методики. Затем щелкнуть на кнопке Мастер диаграмм, расположенной на стандартной панели инструментов. Используя ряды данных А, В и С можно построить График. Чтобы построить Линию тренда, необходимо выделить ряд данных диаграммы, а затем выбрать команду Вставка и Линия тренда. Для того, чтобы вывести на график уравнение тренда, необходимо в меню Линии тренда в параметрах отметить пункт показывать уравнение на диаграмме.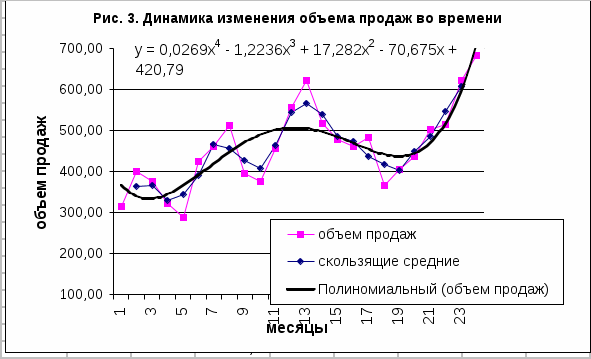


2.Используя функции ТЕНДЕНЦИЯ или РОСТ построить прогнозирующую функцию.

Функция ТЕНДЕНЦИЯ вычисляет прогнозы, основанные на линейной связи между результатом наблюдения и временем, в которое это наблюдение было зафиксировано. Если взаимосвязь между объемом продаж (y_t) и t носит линейный характер, то линия на графике будет либо прямой, слегка наклоненной в одну или другую сторону, либо горизонтальной. В случае, когда линия скользящей средней приближается к прямой, можно использовать функцию ТЕНДЕНЦИЯ.

Если линия резко изгибается в одном из направлений, то это означает, что взаимосвязь показателей носит нелинейный характер. Существует большое количество данных, которые изменяются во времени нелинейным способом. В случае нелинейной взаимосвязи функция Exel РОСТ поможет получить более точный прогноз.

Чтобы использовать функцию ТЕНДЕНЦИЯ, необходимо выделить ячейки D2:D25 и ввести следующую формулу, используя формулу массива:
= ТЕНДЕНЦИЯ (В2:В25;А2:А25)

Для ввода формулы массива надо нажать комбинацию клавиш < Ctrl+Shift+Enter>.

Чтобы использовать функцию РОСТ, необходимо выделить ячейки E2:E25 и ввести следующую формулу, используя формулу массива:
= РОСТ (В2:В25;А2:А25)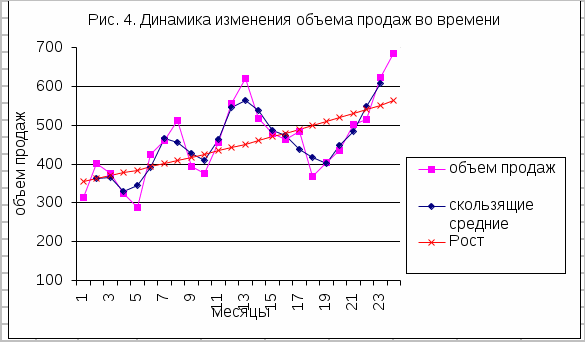



3. Используя функции программы Excel, посчитать доверительные интервалы для 25-ого месяца.

Вычислим по формуле прогнозирующей функции для t = 25

y₂₅ = 844,23

Доверительные интервалы для индивидуальных значений объема продаж рассчитываются по формуле:

y_t^в(н) = ± ∆t ,

то есть необходимо посчитать ∆t.

Для того, чтобы посчитать доверительные интервалы, воспользуемся функцией ДОВЕРИТ из программы Exel. Формат функции ДОВЕРИТ записывается следующим образом:

ДОВЕРИТ( альфа; стандартное отклонение; размер),

где (1- альфа) – значение вероятности, с которой значение y_t+1 попадет в доверительный интервал, для нашего примера P = 0,99 следовательно 1 – альфа =0,99; альфа = 0,01;

стандартное отклонение – это σ_общ , где σ²_общ = - общая дисперсия, учитывающая отклонения исходных значений y_tот средней арифметической y_ср.

размер – это размер выборки.

Вычислим

y_ср = = 10971 : 24= 457,125;

σ²_общ = = 228956,63/24=9539,86;

σ_общ = 97,67;

n = 24

В ячейке вводим функцию ДОВЕРИТ (0,01; 97,67; 24);

В результате ∆t =51,36