Прогнозирование принятия управленческих решений.. Методические указания по изучению курса 7 Варианты контрольной работы 9 Рекомендации по выполнению контрольной работы 12
 Скачать 1.95 Mb. Скачать 1.95 Mb.
|
|
Пример 2.4. Используем исходные данные предыдущего примера (табл. 2.3) и построим экспоненциальный тренд. Определим параметры aи bдля экспоненциального тренда yt= aebt . Необходимо сделать замену переменных: lnyt=lna+bt; lnyt=yt’; lna =a’; Составим систему нормальных уравнений: yt’=n a’ + bt, yt’t = a’t + bt2 Результаты промежуточных вычислений запишем в таблице 2.5. Таблица 2.5
Д Определив все суммы и подставив их в систему нормальных уравнений 168,52= 17 a’ + b ·153 1545,00= a’ ·153 + b ·1785, найдем параметр a’ =9,288 и параметр b = 0,069. Но так как делали замену переменных a=exp(a’), поэтому необходимо вычислить a: a=exp(9,288) =10809. Таким образом, прогнозная модель имеет вид ўt= 10809 e0,069t График исходного ряда и экспоненциального тренда показан на рис.2.3. 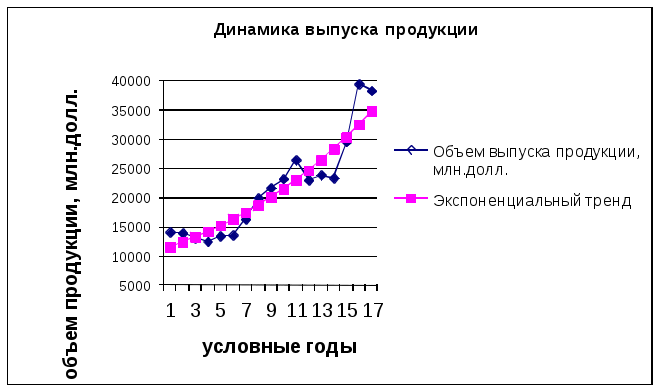 Рис. 2.3. Динамика выпуска продукции Пример 2.5. Для примера 2.4 (изменение объема выпуска продукции) можно найти параметры линейной регрессии на персональном компьютере (ПК) с помощью электронной таблицы (любой ПК совместимый с IBM PC, программа Excel в составе MS Office). Надо использовать встроенную статистическую функцию ЛИНЕЙН. Порядок вычислений следующий: ввести исходные данные или открыть существующий (в формате Excel) файл, содержащий анализируемые данные (рис.4); выделить область пустых ячеек 5х2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики; необходимо активизировать Мастер функций; в окне Категория выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкнуть по кнопке ОК (рис.2.4); заполнить аргументы функции: 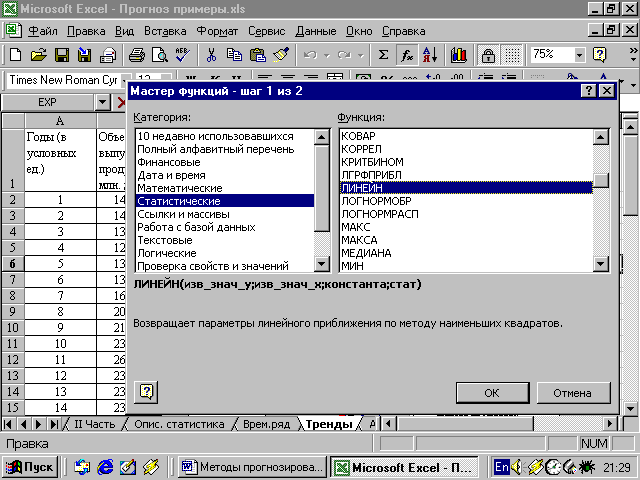 Рис.2.4. Диалоговое окно «Мастер функций» Известные значения y – диапазон, содержащий данные результативного признака; Известные значения x – диапазон, содержащий данные факторов независимого признака; Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 0, то свободный член равен 0; Статистика - логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика =0, то выводятся только оценки параметров уравнения. Щелкнуть по кнопке ОК (рис. 2.5); 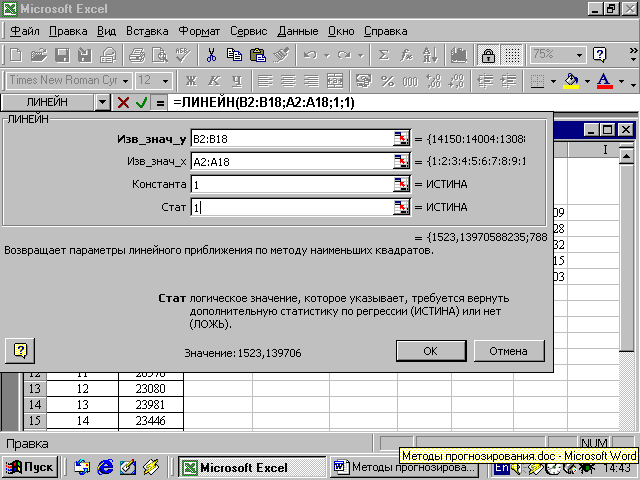 Рис.2.5. Диалоговое окно ввода функции ЛИНЕЙН В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем – на комбинацию клавиш CTRL + SHIFT +ENTER. Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме: Таблица 2.6
Для данных из таблицы 2.5 результат вычисления представлен на рис.2.6.
Рис.2.6. Результат вычисления функции ЛИНЕЙН Для вычисления параметров экспоненциальной кривой yt= aebt в Excel применяется встроенная статистическая функция ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН. Результат вычисления параметров экспоненциального тренда представлен на рис 2.7.
Рис.2.7. Результат вычисления функции ЛГРФПРИБЛ. Построение графика исходного ряда и различных трендов можно осуществлять с помощью Мастера диаграмм. Порядок построения следующий: введите исходные данные или откройте существующий файл, содержащий анализируемые данные; активизируйте Мастер диаграмм; в окне Тип выберите График; вид графика выберите в поле рядом со списком типов. Щелкните по кнопке Далее; заполните диапазон данных в столбцах. Щелкните по кнопке Далее; заполните параметры диаграммы, названия диаграммы и осей, параметры легенды и подписи данных. Щелкните по кнопке Далее; укажите место размещения диаграммы. Щелкните по кнопке Далее. Появится график исходного ряда. Теперь в область диаграммы можно добавить линии тренда: выделите область построения диаграммы; в главном меню выберите Диаграмма/ Добавить линию тренда; в появившемся диалоговом окне выберите вид линии тренда и задайте соответствующие параметры. В качестве дополнительной информации на диаграмме можно отобразить уравнение регрессии и значение среднеквадратического отклонения, установив соответствующие флажки на закладке Параметры. Щелкните по кнопке ОК. На рис.2.8 представлен исходный ряд и тренды с параметрами. 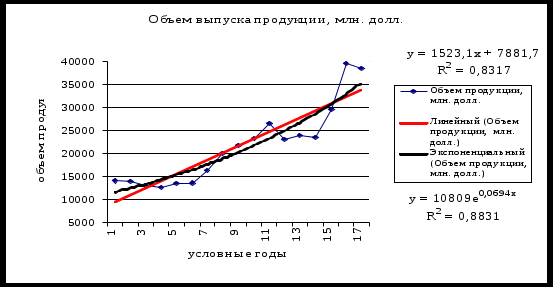 Рис.2.8. График выпуска продукции и трендов Сравним значения R2для линейного и экспоненциального тренда: линейный тренд - R2 = 0,8317; экспоненциальный тренд - R2 = 0,8831. Таким образом, исходные данные лучше описываются экспоненциальным трендом. Следовательно, в данном примере для расчета прогнозных значений лучше использовать экспоненциальный тренд. Расчет возможной ошибки прогноза. Прогнозные расчеты, выполняемые с использованием элементов одиночного временного ряда, завершаются его верификацией, то есть оценкой его достоверности. Отклонения обычно возникают из-за двух основных причин: На зависимую переменную воздействует не только аргумент t, но и множества других факторов, не включенных в явном виде в уравнение прогноза. Иными словами речь идет о случайных ошибках. Элементы исходного динамического ряда в большинстве случаев представляют собой выборку (выборочную совокупность) из некоторой более общей (генеральной) совокупности. Генеральная совокупность – полное множество всех единиц, характеризующих исследуемое явление. Для определения статистической значимости (достоверности) параметров уравнения прогноза принято рассчитывать доверительную зону выборочной линии регрессии (прогноза). Считается, что в рамках этой зоны наряду с линией прогноза ўt=f(t), построенной по выборочным данным, располагается линия регрессии, которую можно получить, если использовать в процессе вычислений элементы всей генеральной совокупности. Чем шире доверительная зона, тем существеннее различия в параметрах выборочной и генеральных линий регрессии. Порядок построения доверительной зоны Построим доверительную зону на примере линейной зависимости yt = a + bt. Сначала определяются случайные ошибки для параметров a и b. Расчеты ведутся по формулам: 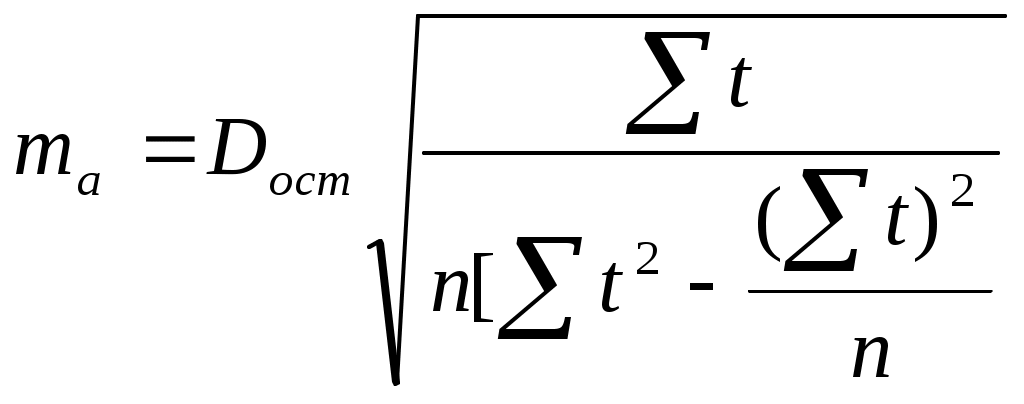 ; (2.16) ; (2.16)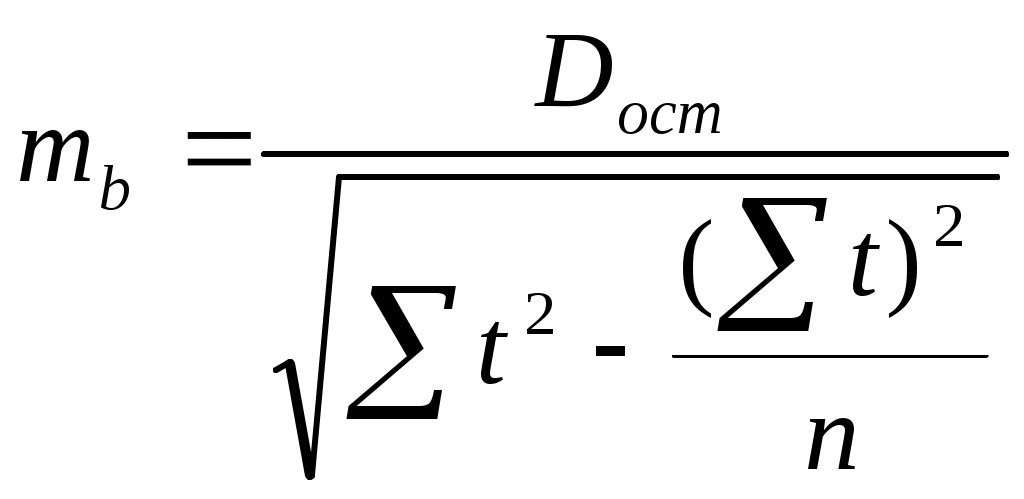 ; (2.17) ; (2.17)здесь ma – случайная ошибка параметра a; mb – случайная ошибка параметра b; D 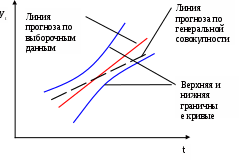 ост – остаточное среднее квадратичное отклонение: Рис. 2.9. Зона доверительной вероятности Чтобы установить, насколько велики расхождения между параметрами уравнений, характеризующих выборочную и генеральную совокупность, можно использовать t – критерий Стьюдента. Фактические значения этого показателя рассчитываются по формулам: Для a Для b Расчетные значения tф сопоставляются с соответствующими табличными величинами tT , найденными для k = n – 2 степеней свободы и принятой доверительной вероятности 0,95 или 0,99. Если tф > tT , то свободный член уравнения тренда a и коэффициент регрессии b считаются статистически значимыми и могут применяться для отображения тенденции изменения переменной yt, сложившейся в генеральной совокупности. Если же tф < tT, то возможность несовпадения закономерностей в выборочной и генеральной совокупностях весьма велика. Выводы Методы непосредственной экстраполяции относятся к числу наиболее простых методов прогнозирования. Они основаны на изучении динамики изменения экономического явления в предпрогнозном периоде и перенесении найденной закономерности в будущее. Достоинствами метода является широкая универсальность вычислительной схемы, незначительная трудоемкость расчетного алгоритма. Следует отметить и недостатки – необходимость использования базовых данных за большой промежуток времени, снижение достоверности прогноза при увеличении срока его упреждения. Для прогнозирования используется временной ряд, представляющий собой дискретные значения какого-либо показателя в течении определённого времени, т.е. состоящего из двух значений (yi) - уровней ряда и момента времени (t). Идея метода в том, чтобы найти тенденцию в изменениях признака и продлить эту тенденцию в будущее. Для этого используются кривые, найденные по методу наименьших квадратов и подобранные по специальным статистическим характеристикам. В конце рассчитывается возможная ошибка прогноза. Понятно, что такой прогноз имеет смысл как краткосрочный, на период, в отношении которого можно принять, что характеристики изучаемого явления существенно не изменяются. Это требование часто оказывается реалистичным вследствие достаточной инерционности внешней среды. Однако и большинство прогнозных ошибок связано с тем, что в момент формулирования прогноза в более или менее явной форме подразумевалось, что существующие тенденции сохранятся в будущем, что редко оправдывается в реальной экономической и общественной жизни. Временные ряды помимо простой экстраполяции могут использоваться также в целях более глубокого прогнозного анализа, например, объема продаж. Целью анализа в данном случае является разложение временного ряда продаж на главные компоненты, измерение эволюции каждой составляющей в прошлом и ее экстраполяция на будущее. В основе метода лежит идея стабильности причинно-следственных связей и регулярность эволюции факторов внешней среды, что делает возможным использование экстраполяции. Метод состоит в разложении временного ряда на несколько компонент – формула (2.1). Вопросы для самоконтроля В чём основная идея методов экстраполяции? Что такое тренд? Какая основная вычислительная схема, используемая для построения прогноза с использованием временного ряда? В чем заключаются особенности сглаживания по методу скользящей кривой? Когда применяется сглаживание по методу конечных разностей? Его особенности и формула для вычислений. Что такое метод наименьших квадратов? Приведите вывод системы нормальных уравнений для линейной и квадратичной функции. Какие кривые чаще всего используются для экстраполяции? Попробуйте связать форму кривых с конкретными процессами, происходящими в реальности. Какому процессу больше соответствует та или иная функциональная зависимость? Назовите способы линеаризации кривых. Для чего применяются специальные статистические показатели? Что такое доверительная вероятность и доверительный интервал? По какой схеме рассчитывается возможная ошибка прогноза? Тесты 1.Временной ряд — это … ряд экономических показателей; плотность распределения случайных величин; совокупность числовых величин, характеризующих изменение некоторого показателя во времени. 2. Уравнение линейного тренда … ўt =a t+ bt2; ўt =a+ bt; ўt =a t+ b t2+с t. 3. Параметры прогнозирующей функции a и b определяются с помощью… метода скользящей средней; экспертных методов; метода наименьших квадратов. 4. Полином k-го порядка … ўt =a1 +a2 yt -2 + ... + ak yt -k; ўt =a0 + a1 t+ a2t2 + ... + aktk; ўt =(a1+ a2 + ... + a)tk. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
