Прогнозирование принятия управленческих решений.. Методические указания по изучению курса 7 Варианты контрольной работы 9 Рекомендации по выполнению контрольной работы 12

• Название: Методические указания по изучению курса 7 Варианты контрольной работы 9 Рекомендации по выполнению контрольной работы 12
• Анкор: Прогнозирование принятия управленческих решений
• Дата: 10.12.2022
• Размер: 1.95 Mb.
• Имя файла: ppur.doc
• Тип: Методические указания; #837443
• страница: 7 из 12

Раздел 2.1. Методы непосредственной экстраполяции

Прогнозирование с использованием временных рядов

Простейшими методами прогнозирования на основе статистической информации являются экстраполяционные методы, основанные на анализе временных рядов.

Многие данные исследований, в частности маркетинговых, представляются для различных интервалов времени, например, на ежегодной, ежемесячной и др. основе. Такие данные называются временными рядами.

Под временным рядом (или рядом динамики) понимают совокупность числовых величин, характеризующих изменение некоторого показателя во времени.

Временной ряд (ВР) задается в табличной или графической формах и состоит из двух элементов: числовых значений показателя (y_i) - уровни ряда и момента времени (t), к которым относятся соответствующие уровни. Оба элемента - члены ВР.

Если члены ряда отражают состояние объекта за определенные промежутки времени - ряд называется интервальным, если фиксируют в строго установленные моменты - моментным.

В зависимости от способа изменения переменной y_t возможно построение ВР, состоящего из абсолютных, относительных и средних величин. Относительные уровни динамических рядов можно получить путем деления абсолютных или средних значений на один и тот же элемент ряда, принятый за базу. Возможно получение относительных величин при сравнении каждого уровня с предыдущим.

Особенность динамических рядов в том, что абсолютный уровень каждого члена ряда является одновременно результатом прошлого развития и сходной предпосылкой для экономического роста в будущем.

Если говорить более подробно, то элементы ВР формируются под влиянием как объективных, так и случайных факторов. Поэтому каждый член динамического ряда можно представить в виде:

Y_t = ў_t + y_tc+y_tц+, (2.1)

где ў_t – значение признака, вытекающее из закономерного изменения показателя во времени,

y_tц – циклическая компонента, соответствующая колебаниям относительно долгосрочного тренда под воздействием среднесрочных флуктуаций экономической активности;

y_tc – сезонная компонента, или краткосрочные периодические флуктуации, обусловленные различными причинами (климат, социально-психологические факторы, структура нерабочих дней и т.д.);

_t - случайная компонента, отражающая совокупное действие плохо изученных процессов, не представимых в количественной форме.

Для каждой компоненты рассчитывается параметр, основанный на наблюдавшихся закономерностях: долгосрочном темпе прироста продаж, конъюнктурных флуктуациях, сезонных коэффициентах, специфичных факторах (например для маркетинга – демонстрации товара, мероприятия по стимулированию сбыта и т.п.). Затем эти параметры используют для составления прогноза.

Совокупность значений ў_t за ряд лет выражает тенденцию развития признака во времени, его эволюцию. Эта компонента называется трендом, тенденцией, эволюторной составляющей.

Тренд характеризует общую тенденцию в изменениях показателей ряда. Те или иные качественные свойства развития выражают различные уравнения трендов: линейные, параболические, экспоненциальные, логарифмические, логистические и др. После теоретического исследования особенностей разных форм тренда необходимо обратиться к фактическому временному ряду, тем более что далеко не всегда можно надежно установить, какой должна быть форма тренда из чисто теоретических соображений. По фактическому динамическому ряду тип тренда устанавливают на основе графического изображения, путем осреднения показателей динамики, на основе статистической проверки гипотезы о постоянстве параметра тренда.

Разработка прогнозов на базе ВР происходит в несколько этапов.

Элементы ВР наносятся на координатное поле;

Если графическое построение не дает четкого представления о закономерности изменения признака во времени, то применяются специальные статистические приемы обработки данных (сглаживание по скользящей средней, определение последовательных разностей и пр.);

Выбирают и рассчитывают параметры аналитической функции вида ў_t =f(t), отражающей динамику изменения прогнозируемого показателя y_t во времени.
Сглаживание временного ряда

Отметим, что пункт 2 представленной схемы прогнозирования может выполнять двоякую роль: он может быть как подготовительным этапом для дальнейшей обработки представленных данных (т.е. для выполнения этапа 3 – расчета параметров прогнозирующей функции ў_t), так и служить вполне самостоятельным методом прогнозирования, т.к. он даёт определенное представление о характере тренда. Рассмотрим два способа сглаживания.
Метод скользящей средней

Суть метода состоит в замене фактических значений показателя их усредненными величинами.

Порядок построения. Пусть y1, y2, ..., yn - динамический ряд. Для определения скользящей средней последовательно рассчитывают сумму m (нечетное число) элементов ряда. По отдельным суммам определяют средние арифметические, каждая из которых меняет свою величину (“скользит”) по мере увеличения t. Наиболее часто на практике применяются трех- и пятичленные средние. Формулы расчета:

y_t^’ = (y_t-1 +y_t+y_t+1)/3, t=2,3, ... , (n-1) (2.2)

y_t’ =(y_t-2 + y_t-1 +y_t+y_t+1+ y_t+2)/5, t=3,4, ... , (n-2) (2.3)

Если скользящая средняя определяется по четному числу элементов, то она не может быть приписана реальному значению t. Ее определяют в 2 этапа: сначала находят средние для промежутков (t-1,t) и (t, t+1), а затем полученные величины суммируют и вновь используют для расчета средней. Чаще используется вычисление по 4 членам ряда:
y_t^’ =1/2[(y_t-2+y_t-1 +y_t+y_t+1)/4+(y_t-1+y_t+y_t+1+ y_t+2)/4], t=3,4,.. ,(n-2) (2.4)

Пример 2.1. В таблице 2.1 представлен объем реализации кондитерских изделий торговым предприятием в течение года. Данные нанесены на график рис. 2.1. Как следует из этого графика этот показатель характеризуется достаточно большим разбросом точек. Поэтому применим к нему метод скользящей средней. Результаты расчетов внесены в таблицу 2.1. и показаны на рис. 2.1.
Таблица 2.1.

Месяц (в условных ед.)	Объем реализации конд. изделий, т.	Трехчленные суммы	Трехчленные скользящие средние	Пятичленные суммы	Пятичленные скользящие средние
1	137,3
2	132,2	411,5	137,2
3	142,0	415,1	138,4	689,2	137,8
4	140,9	419,7	139,9	692,2	138,4
5	136,8	418,0	139,3	695,3	139,1
6	140,3	412,4	137,5	687,3	137,5
7	135,3	409,6	136,5	680,1	136,0
8	134,0	403,0	134,3	678,2	135,6
9	133,7	402,6	134,2	673,2	134,6
10	134,9	403,9	134,6	680,6	136,1
11	135,3	412,9	137,6
12	142,7

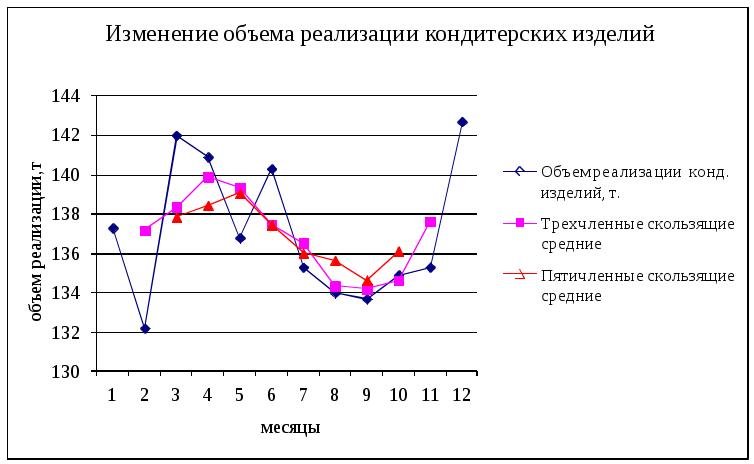Рис. 2.1. График к примеру 2.1.
Метод конечных разностей

Сфера применения - случай, когда динамика изменения исследуемой переменной отображается одним из полиномов k-го порядка:

ў_t =a₀ +a₁ t+a₂t² + ... + a_kt^k (2.5)

Особенность метода - последовательное определение специальных показателей - разностей, среди которых различают разности первого, второго и т.д. порядков:

_t¹ =y_t+1 - y_t (t=1,2,3, ... , n-1); (2.6)

_t²=_t+1¹ -_t¹ = y_t+2 - 2y_t+1 + y_t (t=1,2,3, ... , n-2); (2.7)

_t³=_t+1² -_t² = y_t+3 - 3y_t+2 +3y_t+1 - y_t (t=1,2,3, ... , n-3); (2.8)

и т.д.

В основе метода конечных разностей лежит одно из свойств полинома степени k обращать в нуль разности _t+1^k+1 и придавать одинаковое значение разностям _t+1^k .
Пример 2.2. По данным объема производства хлеба на предприятиях экономического района за 8 лет необходимо определить закономерность выработки продукции за анализируемый промежуток времени. Рассчитаем первые и вторые разности (см. таблицу 2.2).
Таблица 2.2

Год, t	Произведено хлеба yt, тыс. т	Первые разности t1	Вторые разности t2
1	7,6	1,1	0
2	8,7	1,1	0
3	9,8	1,1	0,1
4	10,9	1,2	-0,1
5	12,1	1,1	0
6	13,2	1,1	0
7	14,3	1,1	–
8	15,4	–	–

Как следует из данной таблицы, абсолютные уровни первых разностей для всех значений t являются практически одинаковыми, а величина вторых разностей в большинстве случаев принимает нулевые или близкие к ним значения. Поэтому можно определить зависимость выработки хлеба от времени как полином 1-ой степени, то есть линейную зависимость.
Подбор аналитической функции

Представив в графическом виде данные, можно с помощью метода наименьших квадратов подобрать линию, в наибольшей степени соответствующую полученным данным и определить прогнозную величину исследуемого признака.

Замечание. Строго говоря, подбор аналитической функции нельзя отнести к методу непосредственной экстраполяции. Ведь в данном случае происходит замена временного ряда некой подобранной функцией, т.е. ломаная линия заменяется непрерывной кривой, которую можно рассматривать как некую регрессивную функцию (или математическую статистическую модель). А это значит, что далее мы объединяем метод экстраполяции с методом статистического моделирования.

Метод наименьших квадратов
Рассмотрим метод наименьших квадратов, который находит применение как в экстраполяционных методах прогнозирования, так и в прогнозах с использованием статистического моделирования.

Суть метода наименьших квадратов (МНК) в том, чтобы подобрать параметры уравнения прогноза ў_t = f(t) с таким расчетом, чтобы квадраты суммарных отклонений фактических значений ряда (y_t) от найденных по статистической модели (ў_t) были бы минимально возможными, то есть:
(y_t - ў_t)² = min (2.9)

записав уравнение прямой в виде

ў_t = a+bt

и подставив его в (2.9), получим:

(y_t - a-bt)² =min (2.10)
В рассматриваемом условии минимизации значения переменных y_t и t за предпрогнозный период являются известными, а параметры a и b -неизвестными константами. Для их нахождения надо приравнять нулю частные производные от (2.10) по каждой искомой константе в отдельности. После соответствующих преобразований получают систему уравнений, которую называют нормальной. Для линейного тренда
ў_t = a+bt

нормальные уравнения:
y_t= na + bt,

 (2.11)

y_tt = at + bt²
Подставив в систему (2.11) имеющуюся исходную информацию (y_t и t) рассчитываются параметры прогнозирующей функции а и b. Сомножитель n - длина временного ряда.

Также можно получить нормальные уравнения для квадратичного тренда ў_t = a+bt+сt², которые выглядят так:
y_t=na+bt+сt²,



 y_tt =at + bt² + сt³, (2.12)



 y_tt² =at² + bt³ + сt⁴,
Рассчитав все суммы и решив систему относительно а, b и с, получим уравнение параболического тренда.

Пример 2.3.. В таблице 2.3 представлены данные, характеризующие динамику выпуска продукции Финляндии ( млн долл.) за 17 лет. Провести расчет параметров линейного и экспоненциального тренда, построить графики ряда динамики и трендов.

Таблица 2.3

Условный год	Объем выпуска продукции, млн долл.	ytt	t2	Линейный тренд
1	14150	14150,00	1	9404,883
2	14004	28008,00	4	10928,023
3	13088	39264,00	9	12451,163
4	12518	50072,00	16	13974,303
5	13471	67355,00	25	15497,443
6	13617	81702,00	36	17020,583
7	16356	114492,00	49	18543,723
8	20037	160296,00	64	20066,863
9	21748	195732,00	81	21590,003
10	23298	232980,00	100	23113,143
11	26570	292270,00	121	24636,283
12	23080	276960,00	144	26159,423
13	23981	311753,00	169	27682,563
14	23446	328244,00	196	29205,703
15	29658	444870,00	225	30728,843
16	39573	633168,00	256	32251,983
17	38435	653395,00	289	33775,123
Итого	367030	3924711	1785	367030,051

Для определения числовых значений констант уравнения (2.11) удобно пользоваться таблицей 2.3. Определив все суммы и подставив их в систему нормальных уравнений

367030,0 = 17 a + b 153

3924711,0 = a 153 + b 1785

найдем свободный член уравнения a =7881,74 и коэффициент пропорциональности b = 1523,14. Таким образом, прогнозная модель имеет вид

ў_t = 7881,74 +1523,14  t

Подставляя значения t=1,2…17, получим значения линейного тренда. Нанесем полученные данные на график (рис. 2.2).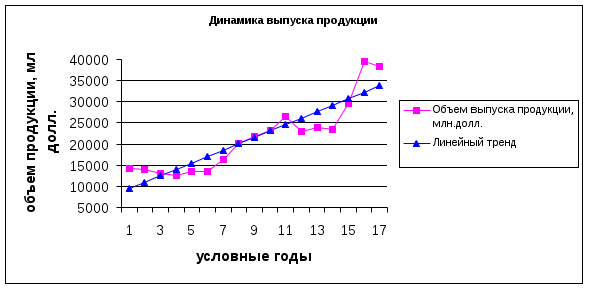




Рис. 2.2 Динамика выпуска продукции
Из графика видно, что изменение выпуска продукции можно приблизить линейной зависимостью.

В случаях, когда в качестве уравнения регрессии используются гиперболическая, экспоненциальная, степенная, логистическая и некоторые другие функции, процессу построения системы нормальных уравнений должен предшествовать процесс линеаризации кривой, осуществляемый с помощью замены переменных (табл.2.4)
Таблица 2.4

Функция	Исходное уравнение	Способы замены переменных	Линеаризованное уравнение
гиперболическая	yt = a+b/t	t’ =1/t	yt’ = a+bt’
степенная	yt=atb	Логарифмируем lnyt=lna+blnt; Lnyt=yt’; Lna =a’; Lnt =t’	yt’ = a’+bt’
Экспоненциальная	yt=aet	Логарифмируем lnyt=lna+t; Lnyt=yt’; Lna =a’;	yt’ = a’+t’’
Логистическая	yt=1/(a+be-t)	1/yt= a+be-t ; 1/ yt= yt’; e-t=t’	yt’ = a’+bt’’
Простая модифицированная экспоненциальная	yt=a-be-t	e-t=t’	yt’ = a’-bt’’

Если для описания исходной кривой с равным основанием можно использовать несколько аналитических функций, то для выбора зависимости, наиболее точно отображающей наблюдаемую динамику, рекомендуется применять специальные статистические показатели. Наиболее распространенные из них: ²_ост-остаточная дисперсия, _ост-среднее квадратичное отклонение, V-коэффициент вариации, r- коэффициент линейной корреляции, R_y/t - индекс корреляции, d -коэффициент детерминации². Первые три показателя связаны между собой:

²_ост= (y – )²/n;

_ост = _; V = ( _ост/y_ср)100%

(здесь y_ср – средняя арифметическая, y_ср= y_t / n).

В качестве уравнения тренда следует использовать ту зависимость, у которой значения ²_ост, _ост, V - минимальны.

Индекс корреляции - дает относительную оценку степени близости тренда к точкам исходной кривой. Общее отклонение фактического значения переменной от среднего уровня можно представить как сумму двух слагаемых:

y_t – y_ср=( y_t – ) + ( – y_ср),

или сокращенно

_общ=_ост+_t,

где _общ – (y_t – y_ср) — отклонение, измеряющее общую вариацию за счет действия всех факторов;

_ост=( y_t – ) — остаточная вариация, характеризующая отклонение между исходным и расчетным значениями переменной y_t;

_t=( – y_ср) — отклонение значения функции от среднего уровня.

Если линия тренда подобрана удачно по отношению к точкам исходной кривой, то

|y_t- |  0. Следовательно:

R_y/t=_t/_общ=(_общ-_ост)/ _общ=1-_ост/_общ (2.13)

По этому уравнению можно оценить близости исходной функции и уравнения регрессии. Чем значительнее разброс точек на графике, тем ниже значение R_y/t, и наоборот.

Формула (2.13) позволяет оценить расхождение для какого-то одного значения аргумента t. Для итоговой оценки надо просуммировать частные результаты по всем годам оцениваемого периода и для устранения влияния знаков отклонения возвести в квадрат. С учетом вышесказанного:
R_y/t= , (2.14)

где – ²_общ=² _общ/n – общая дисперсия, измеряющая вариацию переменной за счет действия всех факторов;

²_ост=² _ост/n – остаточная дисперсия, характеризующая отклонение между ихсодными и расчетными значениями переменной y_t.

Показатель R_y/t принято называть индексом корреляции. Частный случай индекса корреляции - коэффициент линейной корреляции, который определяется для оценки силы связи при линейном взаимодействии признаков ( =a+bt ). Он вычисляется по формуле (2.14) или по некоторым другим и принимает значения -1  r  1. Отрицательное значение r показывает на обратную связь между признаками, положительное - на прямую связь между ними.

Наряду с коэффициентом корреляции применяется коэффициент детерминации:
d=r² (2.15)

Он показывает, какая часть общей колеблемости зависимой переменной y_t объясняется действием фактор-аргумента t.