Прогнозирование принятия управленческих решений.. Методические указания по изучению курса 7 Варианты контрольной работы 9 Рекомендации по выполнению контрольной работы 12

• Название: Методические указания по изучению курса 7 Варианты контрольной работы 9 Рекомендации по выполнению контрольной работы 12
• Анкор: Прогнозирование принятия управленческих решений
• Дата: 10.12.2022
• Размер: 1.95 Mb.
• Имя файла: ppur.doc
• Тип: Методические указания; #837443
• страница: 3 из 12

4. Рекомендации по выполнению контрольной работы

1. Построить график изменения объемов продаж.

При построении графика используется понятие временного ряда. Каждая точка из таблицы строится на координатном поле:

x = t (месяцы),

y = V (объём продаж).

2. Применить метод трёхчленной скользящей средней.

Метод скользящей средней используется для сглаживания эмпирических кривых. Метод основан на замене фактических показателей их усредненными величинами. В зависимости от периода усреднения различают скользящие средние, рассчитанные для нечетного и четного чисел интервалов времени. Количество членов в скользящей средней определяется количеством усредняемых точек.

Кроме того, из-за сглаживания происходит выравнивание контура исходной кривой, что позволяет визуально определить тенденцию изменения показателя, т.е. по внешнему виду полученной кривой сделать предварительный прогноз.

Исходя из вышесказанного, значения трехчленных скользящих средних для трех членов ряда вычисляются по формуле:

=( y_t-1+ y_t+ y_t+1)/3, t = 2, 3,…, ( n - 1), (1)

y_t-1, y_t , y_t+1 – выбираются из построенного графика п.1.
3. Построить систему нормальных уравнений и рассчитать константы прогнозирующей функции

После построения исходной кривой и сглаживания её скользящей средней необходимо построить некую прогнозирующую функцию. Для этого применяется много разных методов, составляющих основу регрессионного анализа. В этом анализе одним из самых простых и наиболее применимым является метод наименьших квадратов. Особенность этого метода в том, что он позволяет подобрать параметры уравнения прогноза = f (t) с таким расчетом, чтобы суммарные отклонения фактических значений ряда (y_t) от найденных по статистической модели были бы минимально возможными. При использовании метода наименьших квадратов для устранения возможности взаимного погашения величин, имеющих разные знаки, отклонения y_t – сначала возводят в квадрат, после чего суммируют. Аналитическая функция = f (t) наиболее точно отображает исходную зависимость, если выполняется условие

( y_t – )² = min (2)

Для определения конкретного вида аналитической функции, используемой в качестве уравнения прогноза, необходимо определить параметры, определяющие её вид.

Например, если для прогноза выбирается линейная функция

= a + bt, (3)

то для определения параметров a и bнеобходимо решить систему двух линейных уравнений с двумя неизвестными. Такая система получается из условия минимальности функции и называется системой нормальных уравнений. Подробно этот процесс описан в [1]. Здесь же просто отметим, что для уравнения тренда (3),называемого также уравнением регрессии,нормальные уравнения имеют вид:

 y_t = an + b t

 y_t t= a t + b t² (4)

Подставив в систему уравнений, имеющуюся исходную информацию (y_tи t), можно рассчитать параметры прогнозирующей функцииaиb. Сомножитель nв первом нормальном уравнении обозначает длину временного ряда. Кроме того, ясно, что для решения этой системы необходимо посчитать все суммы, входящие в уравнения (4).

Для нелинейных функций, например логарифмической, степенной, экспоненциальных и других (данных в настоящем задании в таблице исходных данных) процессу построения системы нормальных уравнений предшествует этап линеаризации кривой, предусматривающий переход от нелинейных связей к линейной зависимости изменения признака. С этой целью осуществляется замена переменных, исходя из соотношений, приведенных в таблице 3.
Таблица 3

Функция	Исходное уравнение	Способы замены переменных	Линеаризованное уравнение
Гиперболическая	yt = a + b/t	t1=1/t	yt=a+bt1
Логарифмическая	yt= a + blnt	t1= ln t	yt=a+bt1
Степенная	yt= atb	1. Логарифмируем lnyt = lna + blnt 2. Обозначим yt1= lnyt a1 = ln a; t1=lnt	yt1= a1 +b t1
Экспоненциальная	yt= aebt	1. Логарифмируем lnyt = lna + bt 2. Обозначим yt1= lnyt 3. a1 = ln a	yt1= a1 +b t

Для случая параболической прогнозирующей функции замена не производится. Системы нормальных уравнений для всех приведенных функций даны в таблице 4.

Таблица 4

Функция	Система нормальных уравнений
Гиперболическая yt= a + b/t	 yt = an + b t1  yt t1 = a t1 + b t12
Логарифмическая yt= a + blnt	 yt = an + b t1  yt t1 = a t1 + b t12
Степенная yt= atb	 yt1= a1 n + b t1  yt1 t1 = a1 t1 + b t12
Экспоненциальная yt= aebt	 yt1= a1 n + b t  yt1t= a1 t + b t2
Параболическая yt=a + bt + ct2	 yt = an + b t + c t2  yt t= a t + b t2 + c t3  yt t2= a t2 + b t3 + c t4

Как видно из таблицы 4 все системы нормальных уравнений (кроме параболической функции) сводятся к системе (4). Отличаются они только заменёнными переменными. В случае параболической функции необходимо решить систему из трёх уравнений, т.к. помимо параметров a и b появляется ещё параметр с.
4. Определить наиболее вероятные объемы продаж в 13, 14 и 15 месяцы

После того как мы получили прогнозирующую функцию, смело можно прогнозировать развитие процесса в будущем. Для этого надо просто подставить в полученную формулу (уравнение функции таблицы 4) значения t = 13, 14, 15.
5. Оценить правильность подбора прогнозирующей функции с помощью остаточной дисперсии, остаточного среднеквадратического отклонения и индекса корреляции

Если для описания исходной кривой с равным основанием можно использовать несколько аналитических функций, то для выбора зависимости наиболее точно отображающей наблюдаемую динамику, рекомендуется применять специальные статистические показатели. В контрольной работе студент использует для сравнения с заданной ему функцией линейную функцию (см. пример выполнения контрольной работы).

В частности, к числу таких статистических показателей относятся: остаточная дисперсия σ²_ост, остаточное среднеквадратическое отклонение σ_ост , коэффициент вариации V и индекс корреляции R_y/t.

Первые три показателя используются очень часто во многих дисциплинах, так или иначе связанных с обработкой статистической информации. Они тесно связаны между собой и рассчитываются по следующим формулам:

σ²_ост= ( y_t– )²/ n ; (5)

σ_ост= ; V= ( )* 100%, (6)

где y_ср - средняя арифметическая,

y_ср = (7)

В качестве уравнения тренда (т.е. прогнозирующей функции) следует использовать ту аналитическую зависимость, для которой σ²_ост , σ_ост и V принимают минимально возможные значения.

Индекс корреляции Ry/t даёт относительную оценку степени близости линии регрессии к точкам исходной кривой. С его помощью можно оценить не только качество подбора линии прогноза к точкам исходной кривой, но и определить силу (тесноту) корреляционной связи, её близость функциональной зависимости. Он вычисляется по следующей формуле:

Ry/t = 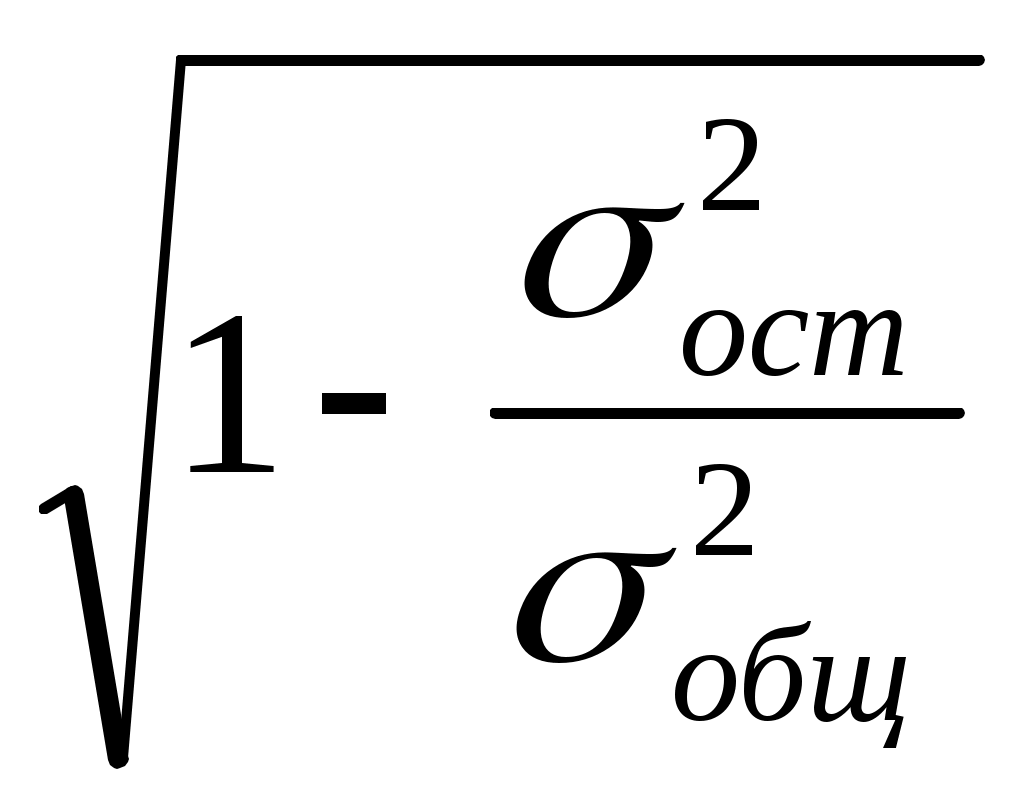, (8)

где σ²_общ = - общая дисперсия, измеряющая вариацию переменной за счет действия всех факторов;

σ²_ост - остаточная дисперсия, характеризующая отклонение между исходными и расчетными значениями переменной y_t .

Чем больше индекс корреляции, тем ближе корреляционная связь к функциональной и тем сильнее взаимодействие между переменными t и y_t. И наоборот, чем в большей степени Ry/t приближается к нулю, тем менее чётко выражена тенденция изменения показателя y_t во времени.

Сила связи между переменными считается слабой при Ry/t =0  0,3; умеренной при Ry/t = 0,3  0,5; заметной при Ry/t = 0,5  0,7; высокой при Ry/t = 0,7  0,9; весьма высокой при Ry/t = 0,9 и более.