Прогнозирование принятия управленческих решений.. Методические указания по изучению курса 7 Варианты контрольной работы 9 Рекомендации по выполнению контрольной работы 12
 Скачать 1.95 Mb. Скачать 1.95 Mb.
|
|
Раздел 2.2. Статистическое моделирование Общие положения Как говорилось в предыдущем разделе сущность методов прогнозной экстраполяции заключается в изучении динамики изменения экономического явления в предпрогнозном периоде и перенесения найденной закономерности на некоторый период будущего. Обязательным условием применения экстраполяционного подхода в прогнозировании следует считать познание и объективное понимание природы исследуемого процесса, а также наличие устойчивых тенденций в механизме развития. Этот способ обладает определенными достоинствами, среди которых незначительна трудоемкость вычислительного алгоритма, универсальные расчетные схемы. Кроме указанных достоинств, он имеет несколько существенных недостатков, о которых говорилось в предыдущем разделе. Распространенной методикой прогнозирования тех или иных процессов и явлений служит моделирование. Моделирование считается достаточно эффективным средством прогнозирования возможного явления новых или будущих технических средств и решений. Впервые для целей прогнозирования построение операционных моделей было предпринято в экономике. Модель конструируется субъектом исследования так, чтобы операции отображали характеристики объекта, существенные для цели исследования. Поэтому вопрос о качестве такого отображения - адекватности модели объекту - правомерно решать лишь относительно определенной цели. Конструирование модели на основе предварительного изучения и выделения его существенных характеристик, экспериментальный и теоретический анализ модели, сопоставление результатов с данными объекта, корректировка модели, составляют содержание метода моделирования. Важным классом математических моделей, имеющих прикладное значение в прогнозировании, являются статистические модели, среди которых основное место принадлежит методам регрессионного и корреляционного анализа. Регрессионный анализ используется для исследования форм связи, устанавливающих качественные соотношения между случайными величинами изучаемого случайного процесса. Достоинством регрессионного метода следует считать его универсальность, широкий выбор функциональных зависимостей, возможность включения в статистическую модель в качестве самостоятельной переменной фактора времени. Отличие методов статистического моделирования от экстраполяционных является построение прогнозной модели, характеризующей зависимость изучаемого параметра от ряда факторов на него влияющих, в то время как методы экстраполяции базируются на прошлом опыте, который продлевается в будущее. Основой этих методов является понятие корреляционной связи. Корреляционная связь - неполная статистическая связь, при которой каждому отдельному значению независимой переменной может соответствовать определенное множество значений функции. Для начала рассмотрим т.н. автокорреляционные статистические модели. Замечание. Отметим важную особенность применяемых моделей (как автокорреляционных, так и двух- и многофакторных). В них мы используем не просто некие показатели y, x и т.п., которые необходимо спрогнозировать. Данные модели мы усложняем тем, что в качестве показателей мы рассматриваем временные ряды, уже известные нам по предыдущему разделу. Это сделано для того, чтобы показать единство процессов прогнозирования, основанных на математической статистике. Иными словами, если наблюдается изменение показателей y и x по времени (т.е. yt = f1(t), xt = f2(t)), то после попыток непосредственного экстраполирования можно применить к ним статистическое моделирование. 2.2.1. Авторегрессионные модели прогнозирования Понятие авторегрессии При прогнозировании некоторых показателей следует учитывать наличие устойчивой связи исследуемого признака с его значениями в прошлом и будущем. Например, реализация винными заводами продукции зависит не только от урожая этого года, но и от направления использования виноматериалов в будущем (сколько закладывается для дальнейшего хранения). Взаимосвязь между последовательными элементами динамического ряда представляет частный случай корреляционной зависимости и носит название автокорреляции. Уравнение, выражающее величину переменной yt для времени t через значения этой переменной в моменты (t-1), (t-2), (t-3), ... , (t-p), называется уравнением авторегрессии. Уравнение авторегрессии в линейной форме: В качестве аргумента и функции в (3.1) используется одна и та же переменная. Уравнение авторегрессии (УА) принято классифицировать по количеству элементов, включенных в правую часть (3.1). Различают уравнения авторегрессии первого порядка (2.2), второго порядка (2.3), уравнения порядка p. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . В общем случае процесс формирования прогноза с помощью УА делиться на 3 стадии: устанавливается порядок УА; определяются параметры прогнозирующей функции; рассчитываются значения переменной yt на перспективу. Определение порядка уравнения авторегрессии Итак, уравнение авторегрессии имеет вид (2.20), но какой порядок это уравнение будет иметь в каждом конкретном случае, является первой стадией формирования прогноза. Для решения этой задачи используются несколько методов. Рассмотрим два из них. Графический анализ исходных данных Это наиболее простой приближенный метод. Строится несколько графиков, по осям которых откладываются соответствующие пары значений (yt, yt-1), (yt, yt-2), (yt, yt-3) и т.д. Интервалы времени (t, t-k), (где k=1,2,3,...), характеризующие удаленность сопоставимых уровней ряда друг от друга, принято называть продолжительностью запаздывания (задержки). Период запаздывания k показывает, через какой промежуток времени изменение переменной yt-kокажет воздействие на yt . Изучение графических построений для разных k позволяет приближенно оценить направление и силу связи между близлежащими членами ряда. Пример 2.6.. Имеются данные о ежесуточной выработке хлебобулочных изделий на одном из хлебопекарных предприятий (табл.2.7). Требуется выполнить графический анализ исходной информации. Таблица 2.7.
Процесс производства и реализации хлеба может быть описан уравнением авторегрессии, поскольку сбыт продукции в произвольно выбранный день в значительной степени зависит от объема реализации в предшествующие периоды. Изучение динамики изменения переменной yt свидетельствует о стационарном варьировании показателя относительно среднего уровня: Построим по этим данным два графика: с запаздыванием переменных yt - 1 и yt и yt - 2 и yt (т.е. k = 1 и k = 2). Необходимые данные для построения представлены в таблице 2.7, а полученные графики на рисунках 2.10 (а и б). 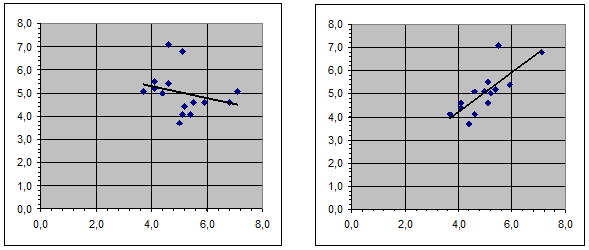 Рис. 2.10 а) Взаимодействие б) Взаимодействие переменных переменных yt - 1 и yt yt -2 и yt Как видно из графиков, между соседними элементами временного ряда существует достаточно сильная корреляционная зависимость (линия тренда – обратная для k = 1 и прямая для k = 2). Наличие автокорреляции означает, что увеличение выработки хлеба в момент времени t (yt yср) повышает обеспеченность населения хлебобулочными изделиями и влечет сокращение продукции на следующий день (k = 1). Спустя сутки (k = 2) ситуация изменяется. Вновь появляется спрос на хлебобулочные изделия и выпуск продукции возрастает. Автокорреляционное взаимодействие можно обнаружить и тогда, когда запаздывание k = 3,4.5. … суткам. Однако, по мере увеличения k зависимость между переменными yt - k и yt становится менее строгой, а разброс точек на координатном поле все более возрастает. Следовательно, период запаздывания применительно к условию решаемой задачи можно принять равным двум дням. Прогнозная модель авторегрессии должна иметь вид: Исчисление автокорреляционной и частной автокорреляционной кривой Для уточнения характера автокорреляционной функции необходимо для каждого возможного интервала запаздывания определить с помощью коэффициента автокорреляции (rk) силу автокорреляционной связи: rk = ck/c0 , (2.24) где ck= c0= Совокупность найденных значений rk образует автокорреляционную функцию, показывающую как изменяется коэффициент автокорреляции по мере увеличения периода запаздывания. При нахождении автокорреляционной функции коэффициенты автокорреляции рекомендуется определять для периодов запаздывания в диапазоне 1 < k n/4. Пример 2.7. Для предыдущего примера рассчитаем коэффициенты корреляции для задержек k = 1, 2, 3, … , 10. Для этого используем таблицы 2.7 и 2.8, дополним их результатами вычислений. Таблица 2.8
Автокорреляционная функция характеризуется тенденцией к уменьшению (“затуханию”) абсолютных значений rk по мере увеличения периода запаздывания k. Из этого следует, что рассчитывать следует автокорреляционные связи, которые характеризуют взаимосвязь уровней ряда, находящихся в непосредственной близости друг от друга. Это наглядно показано на рис. 2.11. 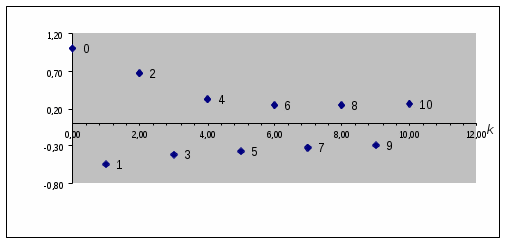 Рис. 2.11. Результат вычисления автокорреляционной функции rk | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
