Корнейчук Б.В. - Микроэкономика. Деловые игры (учебное пособие). Микроэкономика деловые игры
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
|
Рис. 15.1. Первый этап: целевые сегменты рынка * Вторая фигура (клетка Е5) образована пересечением целевых сегментов фирм Ф1, Ф4 и Ф6. Емкость этой клетки равна 16, поэтому каждой фирме достанется треть этой величины, т. е. объем спроса, равный 5,3. * Третья фигура (клетка ЕЗ) образована пересечением целевых сегментов фирм ФЗ и Ф6. Емкость этой клетки равна 5, поэтому каждой фирме достанется половина этой величины. 4. Первый этап. Рассчитаем емкость целевых сегментов фирм (емкость сегментов фирм Ф2 и Ф5 получены выше): * Фирма Ф1. Емкость сегмента равна 16/3 = 5,3. * Фирма Ф4. Емкость сегмента равна 6 + 6 + 6 + 16/3 = 25,8. * Фирма Ф6. Емкость сегмента равна 9 + 9 + 5/2 + 16/3 - 25,8. * Фирма ФЗ. Емкость сегмента равна 5 + 5 + 5 + 5/2 - 17,5. 5. Второй этап. Участники игры выбрали следующие целевые сегменты (табл. 15.4). Таблица 15.4 Второй этап. Выбор целевых сегментов
Примечания: * Объединились фирмы Ф1 и ФЗ, новая фирма обозначена Ф1 + + ФЗ. * Фирма Ф6 открыла два магазина, основная часть капитала передана в первый магазин Ф6 (1). 6. Второй этап. Исследуем фигуры, образованные пересечением целевых сегментов. Всего имеются три спорные области, на рис. 15.2 они заштрихованы: * первая фигура снова представляет собой квадрат, соответствующий совпавшим целевым сегментам двух фирм с центром в клетке В6. Сейчас это фирмы Ф1 + ФЗ и Ф6 (1). Вся емкость данного сегмента, равная 42, достанется объединенной фирме, поскольку она крупнее (22,8 против 22). Емкость целевого сегмента первого филиала фирмы Ф6 равна нулю; * вторая фигура (клетка D3) образована пересечением целевых сегментов фирм Ф6 (2) и Ф5. Емкость этой клетки равна 5, она достается большей фирме Ф5; * третья фигура (клетки Е1 и ЕЗ) образована пересечением целевых сегментов фирм Ф2 и Ф5. Суммарная емкость этих клеток равна 10. Поскольку капиталы обеих конкурирующих фирм одинаковы (21), то емкость спорной области делится поровну. 7. Второй этап. Рассчитаем емкость целевых сегментов фирм: * Фирма Ф1. Емкость сегмента равна половине емкости сегмента объединенной фирмы, т. е. равна 42/2 = 21. * Фирма ФЗ. Емкость сегмента равна 42/2 = 21 (см. пункт а). * Фирма Ф6. Емкость сегмента равна сумме емкостей сегментов обоих магазинов, т. е. О + 15 = 15. 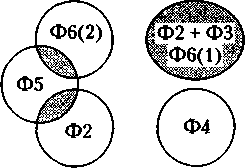 Рис. 15.2. Второй этап: целевые сегменты рынка * Фирма Ф4. Емкость сегмента равна 16 + 6 + 6 + 6 = 34. * Фирма Ф2. Емкость сегмента равна 10 + 9 + 5/2 + 5/2 - 24. * Фирма Ф5. Емкость сегмента равна 3 + 5 + 5 + 5/2 + 5/2 = 18. 8. Итоги игры: * пять баллов и четыре балла не получил ни один участник, поскольку единственная фирма, создавшая филиал, потерпела поражение в конкурентной борьбе с объединенной фирмой в сегменте В6; * три балла получили фирмы Ф2 и Ф4, которые добились емкости целевых сегментов не ниже среднего уровня; * два балла получили остальные фирмы, которые добились ненулевой емкости целевых сегментов ниже среднего уровня. 9. Дадим оценку действиям участников игры: * Фирма Ф1. На первом этапе она получила худший результат, но объединение с другой фирмой на втором этапе позволило ей существенно увеличить объем продаж. * Фирма Ф2. На первом этапе она выбрала лучший сегмент рынка, но фирма-конкурент не позволила ей добиться среднего объема продаж. На втором этапе игры она выбрала менее рискованный сегмент рынка и в борьбе с конкурентами сумела добиться среднего уровня объема продаж. * Фирма ФЗ. Ее действия аналогичны действиям фирмы Ф1. На первом этапе — посредственный результат. На втором этапе — более высокий, полученный благодаря объединению с другой фирмой. Однако основные «плоды» объединения достались другой, более крупной фирме. * Фирма Ф4. На первом этапе она добилась второго по величине объема продаж. На втором этапе сохранила прежний целевой сегмент, а другие фирмы ушли из этого сегмента (не исключено, что из-за солидного капитала фирмы). В итоге фирма заняла первое место по объему продаж на рынке. * Фирма Ф5. На первом этапе она выбрала лучший сегмент рынка, но конкуренция с другой фирмой не позволила ей добиться среднего объема продаж. На втором этапе она выбрала сегмент небольшой емкости, в котором конкурировала сразу с двумя фирмами. В результате она заняла предпоследнее место по объему продаж на рынке. * Фирма Ф6. На первом этапе она выбрала один из лучших сегментов рынка и в конкурентной борьбе с двумя фирмами добилась лидирующего положения на рынке. На втором этапе она решила «покорить» лучший сегмент (В6) и, открыв филиал, получить дополнительно потребительский спрос неосвоенного на первом этапе сегмента (СЗ). Однако она проиграла в конкурентной борьбе за лучший сегмент рынка объединенной фирме и в итоге заняла последнее место по объему продаж на рынке. 16. Деловая игра «Позиционирование товара» Цели игры 1. Усвоить понятия «позиция товара», «позиционирование товара», «параметры позиционирования», «сильная позиция», «близкая позиция», «ценовая политика», «ценовая война». 2. Ознакомиться с табличным способом позиционирования товара в случае двух количественных параметров позиционирования. 3. Приобрести элементарные навыки позиционирования товара, изучения потребительского спроса, выбора ценовой политики в условиях конкуренции. 4. Исследовать особенности позиционирования товара фирмами, вошедшими на рынок в разные периоды времени. Понятия Позиция товара — оценка потребителями места, которое занимает данный товар по отношению к товарам-конкурентам. Позиционирование товара — выбор фирмой позиции для своего товара. Параметры позиционирования — характеристики товара (количественные или качественные), определяющие позицию товара. Сильная позиция товара по отношению к товару-конкуренту — ситуация, когда все параметры позиционирования данного товара не хуже, чем у конкурента. Ценовая политика — регулирование цены товара в целях максимизации прибыли или объема продаж. Ценовая война — ценовая политика, при реализации которой средством достижения цели фирмы служит разорение конкурента. Теория Рассмотрим случай, когда позиция товара задается двумя количественными параметрами, при этом изменение каждого параметра в ту или иную сторону можно трактовать как его улучшение или ухудшение. Например, увеличение жилой площади квартиры можно при прочих равных условиях трактовать как улучшение данного параметра позиционирования. В случае двух количественных параметров позиция товара изображается клеткой таблицы, число строк которой равно числу возможных значений первого параметра, а число столбцов — числу возможных значений второго параметра. Каждой позиции помимо значений параметров, соответствуют три других показателя: • средние издержки производства товара, которые объективно определяются физическими параметрами и считаются заданными; • цена товара, которую устанавливает фирма, следуя той или иной ценовой политике; • потребительский спрос на товар с данными параметрами позиционирования, который, вообще говоря, зависит от установленной цены товара. На рынке число возможных позиций товара существенно превышает число предлагаемых фирмами позиционированных товаров. Поэтому покупатели, предъявляющие спрос на товар с набором параметров, не предложенным фирмам, вынуждены приобретать товар с позицией, наиболее близкой к желаемой позиции. Близкая позиция для данного покупателя есть позиция, предложенная некоторой фирмой. Она определяется по следующему алгоритму: • первый шаг. Определяются позиции фирм, которые не хуже, чем желаемая позиция, т. е. оба параметра позиционирования не хуже желаемых значений. Иными словами, позиция этих фирм «сильнее», чем позиция покупателя; • второй этап. Из выбранных на предыдущем шаге фирм исключаются фирмы с позицией, находящейся слишком далеко от позиции потребителя. Будем считать, что две позиции расположены слишком далеко друг от друга, если они не попадают в некоторый квадрат таблицы, составленный из 16 клеток (со стороной в 4 клетки). Иными словами, если хотя бы для одного параметра позиционирования разность «координат» позиций превышает три единицы; • третий шаг. Обычно выбор потребителем фирмы с близкой позицией завершается на втором этапе. Если все же фирм-претендентов осталось несколько, то выбирается та из них, чья позиция находится на минимальном расстоянии от позиции, желательной для покупателя. Расстояние определяется по теореме Пифагора. Так, если позиция фирмы задается клеткой (9; 6), а желаемая позиция покупателя — клеткой (5; 3), то расстояние между этими позициями равно ((9 - 5)2+ (6 - 3)2)0,5= 5; • четвертый шаг. В редких случаях, когда и после третьего шага осталось несколько фирм, выбирается фирма, установившая минимальную цену. Отметим, что алгоритм может завершиться после выполнения любого шага. Рассмотрим рынок услуг по строительству коттеджей со следующими параметрами позиционирования: • число комнат в коттедже (1,2,..., 8); • расстояние коттеджа от города (10 км; 20 км;..., 80 км). В табл. 16.1 рынок представлен в виде таблицы. Ее строки соответствуют значениям параметра «число комнат», причем эти значения уменьшаются с увеличением номера строки. Это сделано для того, чтобы левый верхний угол таблицы отвечал лучшему типу коттеджа, а правый нижний угол — худшему. Столбцы таблицы соответствуют значениям параметра «расстояние до города», которые расположены в порядке возрастания. В каждой клетке таблицы указаны средние издержки (себестоимость) строительства одного коттеджа (в $ тыс.). Они уменьшаются при перемещении слева направо и сверху вниз — с ухудшением параметров позиционирования. Таблица 16.1 Параметры позиционирования и себестоимость товара
Введем два упрощающих предположения: • потребительский спрос, отвечающий каждой позиции (клетке), равен 10 коттеджам независимо от значений параметров позиционирования и цены товара; • фирма устанавливает единую цену для коттеджей всех типов, близких к выбранной позиции. Эти предположения позволяют не вносить значения потребительского спроса и цены товара в клетки таблицы и существенно упростить вычисления. Так, объем спроса на позиционированный товар фирмы равен числу близких к ней потребительских позиций (клеток), умноженному на 10. При этом прибыль рассчитывается по следующей формуле: П = 10n((р-AСi) + ... + (р-AСn)), где п — число потребительских позиций, близких к позиции фирмы (не превышает 16); р — цена, установленная фирмой, единая для коттеджей всех типов; АСi — средние издержки (себестоимость) строительства коттеджа i-го типа (типы коттеджей нумеруются перемещением по близким потребительским позициям слева-направо сверху-вниз). Пример 1. На рынке есть три фирмы: • фирма А предлагает 5-комнатные коттеджи на расстоянии 40 км от города по цене $27 тыс., ее позиция задается клеткой (5; 40); • фирма В предлагает 3-комнатные коттеджи на расстоянии 50 км от города по цене $18 тыс., ее позиция задается клеткой (3; 50); • фирма С предлагает 7-комнатные коттеджи на расстоянии 60 км от города по цене $30 тыс., ее позиция задается клеткой (7; 60). Определим, какие потребительские позиции (клетки) близки к позиции каждой фирмы в ситуации, когда фирмы конкурируют между собой. Сначала определим, какие потребительские позиции будут близки к позиции фирмы А при отсутствии конкуренции. Для этого построим квадрат 4 х 4 из клеток таблицы, у которого левый верхний угол совпадает с позицией фирмы А (5; 40). Этот квадрат изображает множество близких потребительских позиций в отсутствие конкуренции, т. е. потенциальный спрос на товар фирмы А. Обратимся к фирме В. Ее позиция находится на расстоянии 3 клеток от нижней грани таблицы. Поэтому квадрат 4 х 4 с вершиной в клетке (3; 50) не помещается в таблицу и множество клеток, представляющих потенциальный спрос на товар фирмы, имеет вид прямоугольника с высотой 4 клетки и длиной 3 клетки. В условиях конкуренции конфигурация множеств потребительских позиций, близких к позиции каждой фирмы, определяется характером взаимного пересечения фигур потенциального спроса фирм: квадрата (у фирмы А) и прямоугольника (у фирм В и С). В табл. 16.2 потребительские позиции (клетки), близкие к некоторой фирме, отмечены соответствующей буквой, при этом использован алгоритм определения близкой позиции (см. выше). Четвертый шаг данного алгоритма использован в отношении единственной клетки (5; 60), для которой фирмы А и С предлагают близкие позиции, которые находятся на одинаковом расстоянии от потребительской позиции, равном 3. Потребитель выбирает фирму А, которая установила меньшую цену (27 против 30). Рассчитаем прибыль каждой фирмы. Для этого во всех близких к ее позиции клетках найдем разность цены и средних издержек, суммируем эти разности, умножим полученную сумму на число близких клеток и на 10: а) прибыль фирмы А равна 80 (2 + 4 + 6 + 5 + 7 + 9 + 8 + 11) = 4160; б) прибыль фирмы В равна 120 (1 + 3 + 5 + 7 + 4 + 6 + 8+10 + 7 + + 9 +И+ 13) = 10080; в) прибыль фирмы С равна 100 (3 + 5 + 7 + 8+10 + 11 + 13+14 + 16) = = 9300. В данном случае наибольшую прибыль получила фирма В, предлагающая небольшие коттеджи на значительном удалении от города. Ее позиция оказалась самой выигрышной. Таблица 16.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
