Учебник. московский государственный университет путей сообщения
 Скачать 1.6 Mb.
|
|
Тарификационная система. Наличие даже относительно ограничен-ного числа тарифных факторов, каждый из которых может принимать не-сколько значений, требует формирования большого числа тарифных групп. Возможности современной вычислительной техники позволяют рассчитать для каждой из них свою тарифную ставку. Однако применять такую шкалу, содержащую сотни значений тарифов, на практике неудобно, особенно если продажа страховых услуг осуществляется через агентов. Поэтому развер-нутую таблицу тарифов трансформируют в более компактную и понятную тарификационную систему. Она включает таблицы базовых ставок для наи-более типичных объектов и наборы поправочных коэффициентов, учиты-вающих наличие дополнительных факторов риска по сравнению с выде-ленными типовыми объектами. В общем виде тарификационная система выглядит следующим обра-зом. Все страхуемые объекты делятся на несколько достаточно крупных ка-тегорий на основании двух-трех тарифных факторов. Для каждой категории рассчитывается базовая тарифная ставка. Кроме того, формируется список остальных факторов, которые страховщик хочет отразить в своей системе. Каждому их значению соответствует поправочный коэффициент, который будет применяться к базовым тарифам. Разработку системы тарифов осу-ществляют актуарии. При заключении договора страхования андеррайтер, прежде всего, определяет принадлежность страхуемого объекта к определенной тарифной категории. В соответствии с этим выбирается исходная (базовая) тарифная ставка. Далее определяют значения других тарифных факторов для данного объекта и по таблице находят соответствующие поправочные коэффициенты. Найденные коэффициенты применяются к базовой тарифной ставке. 4.3. Расчет премий по страхованию жизни Особенности актуарных расчетов по страхованию жизни. Стра-хование жизни представляет собой совокупность видов личного страхования, где риск связан со случайным характером продолжительности человеческой жизни. В настоящее время на рынках представлены страховые продукты, существенно различающиеся по своей «конструкции». Условно можно выде-лить две основные группы: – «классические», или «традиционные», страховые продукты, харак-теризующиеся жесткими условиями уплаты премии, гарантированной доход-ностью и фиксированными выплатами; – продукты нового поколения, появившиеся в последней четверти ХХ в., конструкция которых предусматривает гибкие условия в части уплаты премии, а также полный или частичный перенос финансового риска на стра-хователя. Различия в концепции, безусловно, отражаются на расчете страховых премий. В дальнейшем основное внимание будет уделено актуарным рас-четам по традиционным продуктам, которые на текущий момент занимают практически весь отечественный рынок страхования жизни. Исторически формирование страховой или актуарной математики как отдельной отрасли науки во многом обязано именно страхованию жизни. Еще в конце XIX в. на Втором международном конгрессе актуариев была принята Международная система актуарных обозначений, которая применяется в расчетах по стра-хованию жизни и в настоящее время. Существует ряд технических осо-бенностей, отличающих расчеты по страхованию жизни от методов, при-меняемых для рисковых видов. Основным фактором, влияющим на вероятность наступления страхо-вых случаев в страховании жизни, является возраст застрахованного. По-этому для расчета тарифов необходимо знать закон изменения смертности по возрастам. Данные, характеризующие эту зависимость, содержатся в так называемых таблицах смертности, которые составляются на основе демо-графической статистики. Кроме того, подавляющее большинство продуктов по страхованию жизни могут рассматриваться не только как инструмент для защиты от рисков, но и как средство формирования накоплений. Данные накопления инвестируются страховой компанией и приносят определенный доход. Его необходимо учитывать при расчете обязательств сторон. Для этого применяются методы финансовых вычислений. Таким образом, кроме положений теории вероятности в актуарных расчетах по страхованию жизни используются демографическая статис-тика и финансовая математика. В России существует рекомендуемая Ме-тодика расчета страховых тарифов по видам страхования, относящимся к страхованию жизни (утв. Приказом Федеральной службы РФ по надзору за страховой деятельностью от 28 июня 1996 г. № 02-02/18), соответствующая классическим подходам к определению цены страхования. Формирование накоплений по договорам страхования жизни. Практически все виды страхования жизни, кроме некоторых вариантов срочного страхования на случай смерти, заключаются на длительный срок и предусматривают начисление дохода на уплаченные страхователем взносы. Этот доход образуется от инвестирования страховщиком временно свобод-ных средств и при больших сроках страхования может составлять значи-тельную величину. Многие страховые продукты изначально ориентированы не только на покрытие риска смертности, но и на формирование накоплений. Поэтому их часто называют «накопительными». К ним относятся традиционно договоры, включающие страхование капитала или ренты на дожитие. Самые большие накопления обычно имеют место в страховании рент (пенсий, аннуитетов), где они формируются в течение нескольких десятков лет, чтобы обеспечить пожизненные периодические выплаты. В конструкции современных про-дуктов часто предусматривается отдельный накопительный фонд, из кото-рого производятся отчисления на страхование и покрытие расходов стра-ховщика. Средства данного фонда могут инвестироваться в различные фи-нансовые инструменты и приносить доход. Накопления могут формироваться даже в обычном срочном страхо-вании на случай смерти, изначально носящем чисто рисковый характер. С возрастом риск смерти застрахованного увеличивается, и ежегодный взнос должен пропорционально повышаться. Однако это неудобно из коммер-ческих соображений и лишний раз напоминало бы клиентам об увеличении вероятности умереть. Поэтому в классических договорах применяют выров-ненные годовые премии, которые одинаковы в течение всего срока стра-хования. Из-за такого выравнивания в первые годы действия договора их величина оказывается выше, чем фактический уровень риска, а в конечном периоде – ниже. Уплаченные вначале излишки премий накапливаются и покрывают «недобор» взносов в конце срока страхования. Формирование накоплений по договорам страхования жизни делают необходимым учитывать при оценке обязательств сторон возможный доход от их инвестирования. Это осуществляется путем дисконтирования. Дисконтирование. Во многих страховых продуктах гарантируется начисление определенного дохода на накопленные по договору средства. Величина такого дохода, поступающего за год с единицы денежной суммы, называется нормой доходности. Если норма процента составляет i процентов в год, то через год каждая денежная единица превратится в (1 + i). К концу второго года эта сумма составит (1 + i) * (1 + i) = (1 + i)2 и т.д. В общем случае начисление сложных процентов за t лет может быть рассчитано по известной из финансовой математики формуле Будущая стоимость платежа (1 + i)t Современная стоимость платежа 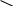 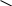 Здесь под будущей стоимостью понимается сумма данного платежа с начисленными по ставке i процентами, которые накопятся за t лет. В страховании жизни взносы и выплаты могут быть разнесены во времени на несколько лет. Чтобы их можно было сравнить, они приводится к одному моменту времени – к моменту заключения договора, т.е. опреде-ляется современная стоимость будущих платежей. Этот процесс называется дисконтированием и описывается формулой Современная стоимость платежа 1/ (1 + i)t Будущая стоимость платежа 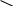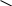Величину, обратную процентному множителю, называют коэффици-ентом дисконтирования и обозначают через v. Дисконтирующий коэффи-циент за t лет определяется по формуле vt = 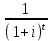 Таким образом, современная стоимость любого платежа, отстоящего от момента заключения договора на t лет, может быть рассчитана как про-изведение его будущей стоимости на дисконтирующий коэффициент за t лет vt Современная стоимость платежа Будущая стоимость платежа Таблицы смертности. Риск в страховании жизни связан со случайной продолжительностью человеческой жизни. Для его оценки необходимо знать вероятности дожития или смерти застрахованных лиц в разных возрастах. Они рассчитываются на основе таблиц смертности, которые показывают для любого возраста х лет число lx доживающих до этого возраста лиц из пер-воначальной совокупности, состоящей из l0 = 100 000 новорожденных (табл. 4.1). Таблица 4.1 Извлечение из таблицы смертности (Российская Федерация. Мужчины. 2006 г.)*
*Источник: http: //www.mortality.org. B данной таблице в первом столбце содержится возраст х лет (от 0 до ω лет с шагом один год, где ω – предельный возраст таблицы смертности), а во втором показано число лиц lx из lo = 100 000 новорожденных, доживающих до этого возраста х лет. В третьем столбце приведено число лиц dx, умирающих при переходе от возраста х лет к возрасту (х + 1) год: dx = lx – lx+1 В таблицах смертности также часто приводятся производные пока-затели. Например, вероятность смерти qx при переходе от возраста х лет к возрасту (х + 1) год, вероятность рх дожития лица в возрасте х лет до возраста (х + 1) год, среднее остаточное время жизни ex в возрасте х лет и др. Даже на основе простейшей таблицы можно определить необходимые для оценки риска вероятности. Например, вероятность nрх дожития лица в возрасте d возрасте х лет до возраста (х + n) лет рассчитывается как отношение коли-чества доживающих до возраста(х+n) лет lx+ n к количеству лиц, доживших до возраста х лет lx: npx= 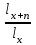 Таблицы смертности составляются на государственном уровне соот-ветствующими статистическими организациями по данным переписи насе-ления страны или отдельного региона. Однако страховым компаниям важнее знать закон смертности среди лиц, которые заключают договоры страхования жизни и пенсионного страхования. Как правило, уровень дохода по данной категории населения несколько выше средних показателей по стране, а смертность ниже. Кроме того, благодаря прогрессу науки и медицины общая продолжительность жизни в мире постепенно растет. Поэтому крупные страховые компании, располагающие достаточным объемом данных о своих клиентах, часто формируют собственные таблицы. Они более точно ха-рактеризуют смертность именно для застрахованных лиц и содержат прогноз относительно ее изменения в будущем. Структура нетто-премии по страхованию жизни. В предыдущих параграфах было показано, что в основе цены страхования лежит рисковая премия. Она отражает риск выплаты, который представляет собой данный договор для компании. По страхованию жизни застрахованными объектами являются люди. Даже с учетом возможных различий в социальном и про-фессиональном плане, а также в состоянии здоровья однородность объектов здесь намного выше, чем в имущественных видах. В одной компании может насчитываться несколько десятков, а то и сотен тысяч застрахованных. Такой страховой портфель, объединяющий огромное количество гомогенных рис-ков, прекрасно подчиняется закону больших чисел. Относительные откло-нения от ожидаемых значений в нем будут незначительны. Поэтому в струк-туре премии по страхованию жизни не предусматривается отдельной риско-вой надбавки, как это имеет место в других видах страхования, где серьезные колебания более вероятны. Компенсация небольших неблагоприятных от-клонений фактических параметров обеспечивается за счет консервативного выбора нормы доходности и таблиц смертности. Изначально занижая га-рантированный доход, компания оставляет себе возможность покрыть слу-чайное превышении выплат за счет разницы между фактической и обе-щанной доходностью вложений. Т Нетто-премия Рисковая премия аким образом, в страховании жизни для больших портфелей нетто-премия равна рисковой премии. Рисковая надбавка неявным образом вклю-чена в рисковую премию Актуарная оценка обязательств. Рисковая премия (и совпадающая c ней нетто-премия) рассчитывается исходя из принципа эквивалентности. Поскольку в страховании жизни приходится учитывать возможный доход от инвестирования, данный принцип применяется в своей общей формулировке: Современная ожидаемая стоимость обязательств страхователя Современная ожидаемая стоимость обязательств страховщика Для применения принципа эквивалентности необходимо рассчитать современную ожидаемую стоимость обязательств, которую также называют актуарной стоимостью, или актуарной оценкой. С финансовой точки зре-ния договор страхования представляет собой ряд взаимных платежей, кото-рые могут осуществиться с определенной вероятностью. Обязательства каж-дой из сторон складываются из всех платежей, которые она должна осу-ществить. В Ожидаемая стоимость платежа Вероятность платежа Номинальная сумма платежа классических продуктах величина выплат и взносов фиксируется еще при заключении договора. Поэтому их номинальные суммы заранее известны и неслучайны. Случайным может являться лишь факт осуществления. Поэтому ожидаемая стоимость каждого платежа равна произведению его номинальной суммы на вероятность: С Современная ожидаемая стоимость платежа Дисконтирующий коэффициент за t лет vt Ожидаемая стоимость платежа овременная ожидаемая стоимость платежа, который планируется осуществить через t лет с момента заключения договора, получается путем умножения его ожидаемой стоимости на дисконтирующий коэффициент за указанный период t: Сложив современные ожидаемые стоимости всех платежей, которые должна произвести сторона договора, мы получим актуарную оценку ее обязательств. Актуарная стоимость обязательств страховщика. Обязательства страховщика заключаются в осуществлении страховых выплат при наступ-лении определенных страховых случаев. В «классическом» страховании жизни основными страховыми рисками являются: дожитие застрахованного лица до определенного возраста или срока, смерть застрахованного в течение срока страхования. Кроме этих рисков в продукты могут быть включены дополнительные гарантии на случай инвалидности или временной нетру-доспособности, страхование от несчастных случаев и т.д. В страховании жиз-ни применяются две формы страховых выплат: – единовременная выплата страховой суммы; – последовательные периодические выплаты (рента, пенсия, аннуитет). Форма выплаты по каждому страховому риску обычно определяется при заключении договора. В современных продуктах также иногда пре-дусматривается возможность выбора между единовременной выплатой или рентой при наступлении страхового случая. В такой ситуации перерасчет осуществляется исходя из равенства актуарной стоимости для всех форм выплат. Страховые продукты, как правило, представляют собой комбинацию нескольких видов ответственности страховщика, т.е. страховых рисков и соответствующих им форм выплат. Наиболее распространенными являются: – единовременная выплата страховой суммы при дожитии до опре-деленного возраста или срока; – единовременная выплата страховой суммы в случае смерти в течение срока действия договора; – выплата страховой ренты (пенсии, аннуитета) при дожитии до опре-деленного возраста или срока. Страхование на случай смерти может осуществляться самостоятельно либо дополнять страхование на дожитие или ренты. Кроме указанных основных видов страхования, в договор могут включаться дополнительные гарантии (возврат взносов в случае смерти застрахованного, освобождение от уплаты взносов, в случае инвалидности и т.д.). Их стоимость также оце-нивается по изложенным выше принципам и учитывается в цене страховой услуги. Коммутационные функции. Расчет тарифов для всех возрастных групп до распространения вычислительной техники был очень трудоемким. Поэтому еще в XVIII в. для упрощения расчетных формул была разработана методика использования так называемых коммутационных функций. В по-следнее время с развитием компьютеров эта методика уже не играет такой важной роли, но она может оказаться полезной при вычислении тарифов в электронных таблицах. Коммутационные функции представляют собой специальные техни-ческие показатели, не имеющие определенного «физического» смысла. Их применение вызвано стремлением сократить объем ручных вычислений. Коммутационные функции рассчитываются на основе выбранной таблицы смертности и нормы доходности для всех возрастов по следующим зави-симостям: Dx = lx * vx; Nx= Dx + Dx+1 +…+Dω; Cx = dx * vx+1; Mx = Cx + Cx+1 +…+ Cω, где ω – предельный возраст таблицы смертности. Перевод выражений для расчета актуарной стоимости обязательств в коммутационные функции осуществляется путем преобразований общих формул после умножения их числителя и знаменателя на vx. B результате, формулы принимают более простой и удобный для вычислений вид nEx = 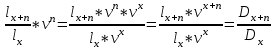 ;nAx = 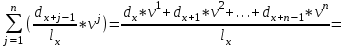 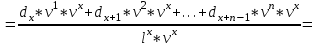 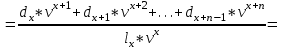 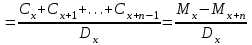 ;m|nax = 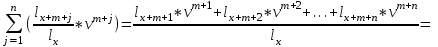 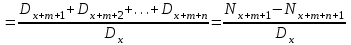 ;m|näx = 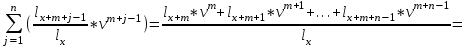 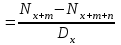 .В табл. 4.2 приведены значения основных коммутационных функций для некоторых возрастов, рассчитанные по российской таблице смертности 2006 г. для мужчин при норме доходности 5% годовых. Таблица 4.2 Фрагмент таблицы значений основных коммутационных функций. Таблица смертности (РФ. Мужчины, 2006 г. при норме доходности 5%)
Р Брутто-премия 100% Страховой тариф, % Страховая сумма 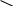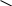асчет единовременной премии по договору страхования жизни. Единовременная страховая (брутто-) премия по договору страхования жизни, также как и в рисковых видах, равна произведению страховой суммы на брутто-ставку: Б Брутто-ставка 1 – f Нетто-ставка рутто-ставка также определяется по формуле, общей для всех видов страхования: Здесь f – заданная доля нагрузки в брутто-ставке. Нетто-ставка определяется исходя из принципа эквивалентности обя-зательств страхователя и страховщика. Обязательства страхователя состоят в уплате единовременной страховой премии. Ее оплата производится пол-ностью в момент заключения договора, поэтому ее современная ожидаемая стоимость совпадает с номинальной величиной. Актуарная стоимость обязательств страховщика будет складываться из современной ожидаемой стоимости всех видов ответственности, предусмот-ренных в договоре. Применив принцип эквивалентности и приравняв оценки обязательств сторон, получаем, что величина единовременной нетто-премии соответствует современной ожидаемой стоимости обязательств страховщика по договору: Единовременная нетто-премия Актуарная стоимость обязательств страховщика ∑ Нетто-премию можно представить как произведение страховой суммы на нетто-ставку. В свою очередь, как было показано ранее, актуарная стои-мость обязательств страховщика равна произведению страховой суммы, под-лежащей выплате, на современную ожидаемую стоимость соответствующих единичных (т.е. величиной в одну денежную единицу) обязательств. Единовременная нетто-ставка Актуарная стоимость единичных обязательств страховщика ∑ Рассчитав актуарную стоимость предусмотренных в договоре единич-ных обязательств по полученным ранее формулам, определяем единовре-менную нетто-ставку, а затем и брутто-тариф. Расчет периодических взносов. Коэффициент рассрочки. Длитель-ный срок и наличие накопительной части в большинстве продуктов по страхованию жизни приводят к тому, что величина единовременной стра-ховой премии может составлять внушительную сумму. Не все страхователи способны сразу уплатить ее. С психологической точки зрения высокая объявленная цена страхования может отпугнуть часть потенциальных кли-ентов. Поэтому в страховании жизни обычно применяют уплату премии в рассрочку в течение нескольких первых лет или даже в течение всего срока страхования. Величина периодического взноса не может быть рассчитана простым делением единовременной премии на количество взносов. При уплате в рас-срочку средства поступают к страховщику по частям. В результате теряется некоторый доход, который мог быть получен от их инвестирования. Кроме того, в течение периода уплаты взносов часть застрахованных может умереть. Это приведет к досрочному прекращению их договоров, и страховая компания недополучит часть запланированных взносов. Данные обстоя-тельства приходится учитывать при определении величины периодических премий. П Периодический взнос Единовременная премия о традиционным договорам страхования размер, количество и момент уплаты взносов фиксируются в договоре. Сумма отдельного платежа рас-считывается путем деления единовременной премии на некоторый коэф-фициент, называемый коэффициентом рассрочки. Коэффициент рассрочки Величина коэффициента рассрочки всегда меньше планируемого ко-личества взносов, поскольку приходится учитывать недополученный доход и смертность застрахованных. В результате сумма рассчитанных таким обра-зом периодических взносов по договору больше величины единовременной премии. В общем случае величина коэффициента рассрочки зависит от перио-дичности и продолжительности уплаты взносов, вероятности смерти застра-хованного и гарантированной доходности. В основе его расчета лежит тот же принцип эквивалентности. Обязательства страхователя здесь приобретают элемент случайности и должны оцениваться не по номинальной, а по со-временной ожидаемой стоимости. Технические особенности страховых продуктов нового поколения. Характерной чертой традиционных страховых продуктов является жесткая однозначная связь между премиями, накоплениями и выплатами по дого-вору. Изменение в течение срока действия одного из этих элементов неиз-бежно ведет к изменению двух других. Например, неуплата очередного взноса приводит к уменьшению накоплений по договору и, как следствие, к снижению страховой суммы. Напротив, начисление дохода сверх гаранти-рованного влечет увеличение страховой суммы и может потребовать повы-шения страховой премии. Все взаимные платежи и доходность по таким продуктам фиксируются заранее на весь срок страхования. Это приемлемо для стабильных условий жизни. Однако в условиях переменчивого совре-менного мира такие жесткие обязательства на продолжительный срок не всегда удобны для всех сторон договора. В конце 70-х гг. ХХ в. под влиянием изменившихся социально-эко-номических условий в развитых странах появились страховые продукты, где связь между премией и гарантированными выплатами не была такой жесткой. В частности, были созданы конструкции договоров, где доход не гарантируется, а зависит от изменения стоимости определенных финансовых инструментов (акций, паев инвестиционных фондов и т.д.). Благодаря такому переносу инвестиционного риска на страхователя исчезла необходимость заранее учитывать в обязательствах страховщика доходность, которая с трудом поддается прогнозированию на длительный период. В других конструкциях продуктов «гибкость» обеспечивается за счет создания в рамках отдельного договора своего накопительного фонда. Страхователь может уплачивать взносы практически в любом размере и в удобный для него момент. После вычета расходов, связанных с уплатой взноса, все оставшиеся средства поступают в данный фонд. Из него с опре-деленной периодичностью производятся ежемесячные вычеты на покрытие расходов страховщика и отчисления на страхование риска смерти. При заключении договора фиксируется лишь максимально возможная величина таких отчислений, а их фактический размер устанавливает сама страховая компания в зависимости от текущей ситуации на рынке и результатов своей работы. Договор может действовать до тех пор, пока средств фонда хватает на все отчисления. Расчеты по таким современным страховым продуктам существенно отличаются от рассмотренных традиционных подходов. В них большое вни-мание уделяется прогнозированию будущих возможных расходов страховой компании и финансовому анализу. |