Учебник. московский государственный университет путей сообщения
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Рисковая надбавка для массовых видов страхования. Как было показано ранее, рисковая премия обеспечивает превышение премий над выплатами с вероятностью лишь 50%. Поэтому к ней делается рисковая надбавка, повышающая вероятность безубыточной работы страховой ком-пании до заданного уровня гарантии безопасности. В отечественной методике расчета тарифных ставок по рисковым видам страхования расчет рисковой надбавки осуществляется исходя из предположения о нормальном распределении совокупной суммы убытков по портфелю, сделанного на основе центральной предельной теоремы. Реко-мендуемая упрощенная формула для расчета рисковой надбавки к нетто-ставке Тр имеет вид To ≈ 1,2*α(γ)*T 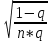 Здесь То - основная часть нетто-ставки, а q - частота страховых случаев. Коэффициент α(γ) учитывает величину гарантии безопасности γ и представляет собой квантиль нормального распределения, при котором Ф(α)= γ. Чем выше требуется гарантия безопасности, тем больше будет α. Например, при гарантии безопасности γ=95% α(γ) = 1,645, а при γ = 98% коэффициент α(γ) равен 2. Кроме того, в рассматриваемом выражении присутствует планируемое количество договоров n. Согласно закону больших чисел при значительном объеме портфеля серьезные отклонения менее вероятны, что позволяет уме-ньшить рисковую надбавку и тариф в целом. Слишком «оптимистичные» прогнозы будущего количества заключенных договоров могут привести к необоснованному занижению тарифных ставок и, как следствие, к нехватке средств страхового фонда. Необходимо также отметить, что данная формула справедлива только для случаев, когда наблюдаемая частота страховых случаев меньше единицы и может служить оценкой вероятности их наступления. Если по договору в среднем ожидается больше одного случая, расчет рисковой надбавки должен осуществляться по другим зависимостям. Кумуляция риска. При выводе формул для рисковой премии и ос-новной части нетто-ставки подразумевалось, что все риски являются неза-висимыми. Это означало, что возникновение убытка по каждому отдельному договору не зависит от наступления страховых случаев с другими объектами. Такое допущение в массовых рисковых видах чаще всего справедливо. Ис-ключение составляют ситуации, когда страховой случай с одним объектом провоцирует наступление убытков по другим договорам. Возникает своего рода «цепная реакция». В итоге совокупная величина выплат, вызванных одним событием, может достигать огромных значений. Такой эффект назы-вается кумуляцией риска. В медицинском страховании данный эффект возни-кает при распространении эпидемий. В страховании имущества примером возможной кумуляции является распространение пожара на соседние объ-екты. Предположим, что значительная часть застрахованных по риску «по-жар» автомобилей (например, 100 из 1000) хранится на одной стоянке. При поджоге одного из них огонь способен перекинуться на другие машины. Одновременно могут пострадать несколько объектов. Для отдельного авто-мобиля вероятность возгорания относительно невелика и составляет обычно менее 0,5%, т.е. ожидаемое число пожаров на 1000 машин не более 5 в год. Если же в результате одного события у одного страховщика сразу сгорело 10-15 автомобилей, то премий, рассчитанных по риску «пожар», просто не хватит на выплаты даже с учетом рисковой надбавки. Чтобы защититься от возможной кумуляции, страховые компании ус-танавливают соответствующие условия приема рисков на страхование, про-водят обследования объектов и т.д. Если совсем избежать кумуляции не удается, применяются другие меры защиты, например перестрахование ката-строфических рисков. Тарифные факторы. Другим важным допущением при выводе фор-мулы для основной части нетто-ставки было предположение об одинаковом уровне риска для всех объектов в группе. Благодаря этому стало возможно применять для них один и тоже тариф. Полученное для его расчета выра-жение справедливо только для однородной (гомогенной) совокупности рис-ков. Если в группе окажутся объекты, сильно отличающиеся по вероятности и тяжести убытков, то премии, определенные на основе усредненного груп-пового тарифа, плохо будут соответствовать фактическому уровню риска. Поэтому все объекты, подлежащие страхованию, стараются разделить на однородные с точки зрения риска категории – тарифные группы. Задача деления на тарифные группы является достаточно сложной и не всегда легко поддается формализации. При ее решении используются раз-личные методы статистического анализа данных, цель которых – выявить факторы, влияющие на степень риска. Для этого оценивается связь (корре-ляции) между различными физическими (наблюдаемыми) характеристиками объектов и параметрами риска. В результате проведенного анализа стра-ховщик получает перечень факторов, которые с высокой степенью досто-верности определяют вероятность наступления страхового случая и (или) ожидаемую величину убытка. Количество факторов риска может оказаться довольно большим. Но между ними часто существует взаимосвязь, и приходится следить, чтобы одно и то же обстоятельство не учитывалось в тарифе несколько раз. На-пример, в процессе анализа результатов по страхованию автотранспорта может быть выявлена зависимость ожидаемого убытка по договору от пола водителя и мощности двигателя. Было бы логично учесть оба этих фактора при расчете тарифов. Однако, как правило, машины, управляемые води-телем-женщиной, имеют меньшую мощность двигателя. Приходится срав-нивать влияние пола водителя при одинаковой мощности, и, возможно, зависимость будет не такой сильной, как казалось вначале. По результатам анализа выделяют некоторый набор независимых наи-более значимых факторов, которые в дальнейшем будут учитываться при расчете тарифов. Их называют тарифными факторами. Объекты, имеющие одинаковые значения данных показателей, будут образовывать однородную с точки зрения риска группу или класс. Количество тарифных факторов и их возможных значений должно, с одной стороны, обеспечивать достаточную однородность объектов в каждой группе, а с другой – не сильно затруднять практическое применение системы. Их увеличение ведет к сокращению чис-ла объектов в каждом классе и может вызвать ухудшение точности статис-тических оценок. Поэтому страховщику при тарификации страхового про-дукта приходится искать компромисс между степенью однородности объек-тов и количеством групп. Дополнительные причины обеспечения однородности групп. Фор-мирование однородных групп при расчете тарифов необходимо не только для соблюдения принципа эквивалентности. Единый тариф, рассчитанный для совокупности объектов с разным уровнем риска, может оказаться недоста-точным для покрытия всех убытков даже с учетом рисковой надбавки. В рамках неоднородной группы объединены договоры, имеющие раз-личные значения вероятности и тяжести убытков. Количество «опасных» и «неопасных» объектов в ней соотносится в некоторой пропорции. Рассчи-танная для такой совокупности усредненная тарифная ставка сможет обес-печить безубыточность страхового фонда только при условии сохранения этой начальной пропорции. Если же из-за изменения рыночной конъюнктуры или маркетинговой стратегии компании доля «опасных» объектов станет больше, убыточность по портфелю окажется выше расчетной и собранных премий уже не хватит на все выплаты. Тарифная политика страховщика существенно влияет на коммерческую сторону деятельности и является одним из основных средств конкуренции. Кроме того, страховые тарифы в комплексе с правилами андеррайтинга и условиями договора являются важным инструментом селекции рисков. Под селекцией здесь понимается отбор страховщиком с помощью различных методов выгодных для себя рисков и «отторжение» неблагоприятных. Это достигается путем создания для «плохих» объектов невыгодных условий страхования, в частности назначением высокой страховой премии. Неправильная тарифная политика при отсутствии других сдерживаю-щих факторов может серьезно ухудшить селекцию рисков. Например, если расчет тарифа в компании происходит по неоднородной группе, то полу-ченная в итоге ставка будет соответствовать «усредненному» уровню риска. Премия перестанет быть «справедливой»: цена по страхованию «опасных» объектов будет ниже, чем их фактический уровень риска, а для «хороших» договоров тариф окажется завышенным. В результате в эту компанию нач-нется приток «неблагоприятных» клиентов, а выгодные риски уйдут к дру-гим страховщикам, где цена эквивалентна риску. Как следствие, убыточность окажется выше расчетной. Подобный эффект отбора неблагоприятных для данного страховщика рисков называется антиселекция. В общем случае она может происходить не только вследствие ошибок в тарификации страховых продуктов. Другими возможными причинами являются непродуманные условия страхования, от-сутствие ограничений на принятие в страхование «опасных» рисков, непра-вильная политика в области продаж страховых услуг. Кроме перечисленных экономических и технических факторов, уста-новление справедливой цены, эквивалентной уровню риска, может стать дополнительным стимулом для принятия страхователем мер, направленных на предотвращение страховых случаев. Клиент окажется перед выбором: оставить свой «опасный» объект как есть и каждый год платить за страховку повышенную премию либо принять дополнительные меры безопасности (установить сигнализацию, организовать охрану и т.д.) и уменьшить тем самым цену страхования. Статистические данные. В рамках однородной тарифной группы предполагается, что все объекты имеют одинаковый уровень риска. При его измерении используются такие численные характеристики, как вероятность наступления страхового случая, ожидаемая величина выплат или тяжести убытков и т.д. Однако в реальной жизни страховщик не знает объективно существующих в природе теоретических значений этих параметров. Все, что он может наблюдать, – это конкретные реализации случайных величин (реальные страховые суммы и ущербы). Возникает потребность оценки объ-ективных показателей с помощью имеющихся статистических данных. Точ-ность такой оценки зависит от количества и достоверности располагаемой информации. Необходимые данные могут быть собраны внутри самой страховой компании или получены из внешних источников (таких, как государственные органы статистики, ассоциации страховщиков, компетентные органы и т.д.). Каждый из указанных источников имеет свои достоинства и недостатки. В частности, внутренняя статистика по договорам страхования позволяет оце-нить не только частоту страховых случаев, средний размер страховой суммы и выплат, но и дисперсию этих показателей, а также вид распределения. Однако объем статистических данных ограничен количеством договоров, заключенных данной компанией по интересующему виду страхования. По-этому весьма вероятны отклонения характеристик, обусловленные малым объемом и недостаточной репрезентативностью выборок. Напротив, оценки показателей, полученные из внешних источников, могут быть более надеж-ны, поскольку основаны на данных по всему городу, району или даже страны. Однако среди них практически никогда не удается найти инфор-мацию о типично страховых показателях, например таких, как отношение ущерба к стоимости пострадавшего имущества. В результате страховой компании для повышения надежности расчетов приходится комбинировать информацию из внешних и внутренних источников. Если расчет осуществляется на основе собственной статистики, пред-варительно производится отбор необходимой информации. Из всего стра-хового портфеля формируется однородная выборка договоров, характе-ристики которых соответствуют интересующей тарифной группе. Объем этой выборки должен быть как можно больше. Тогда в соответствии с за-коном больших чисел можно надеяться, что ее средние значения будут близ-ки к оцениваемым ожидаемым величинам. Кроме того, желательно, чтобы все отобранные договоры действовали в пределах одного и того же периода. Вследствие изменяющейся экономической и политической ситуации, а также из-за инфляции, показатели страховых сумм и выплат, а иногда и частоты страховых событий существенно изменяются во времени. Поэтому рекомен-дуется рассчитывать тарифы на основе данных по недавно закончившимся договорам, например, за прошлый год. Еще одним критерием подбора исходных данных является идентич-ность условий договоров в части определения страховых рисков, сроков страхования и расчета выплат. Они должны быть близки к условиям того страхового продукта, для которого производится вычисление тарифов. Раз-ные способы расчета выплат (например, с применением франшизы и без нее) будут искажать реальную картину убытков и могут привести к необосно-ванному занижению тарифных ставок. На основе сформированного набора исходных данных, удовлетво-ряющего перечисленным требованиям, страховщик может рассчитать стра-ховой тариф для рассматриваемой тарифной группы. Порядок расчета базовых тарифных ставок. По каждой тарифной группе рассчитывается своя тарифная ставка Тб (брутто-тариф). Для этого требуется определить нетто-ставку TH, которая, в свою очередь, складывается из основной части То и рисковой надбавки TP. Основная часть нетто-ставки То равна произведению частоты страховых случаев q на отношение ожи-даемой выплаты к ожидаемой страховой сумме (SB/S). Страховщику необ-ходимо оценить эти параметры на основе имеющейся у него статистики. Предположим, в качестве исходной совокупности было отобрано N дого-воров (по каждому договору застрахован только один объект). Страховые суммы по этим договорам составляли S1, … , Si, … , SN (всего N договоров). Для исходной выборки обычно отбирают закончившиеся договоры, по которым уже известно окончательное количество страховых случаев и сумм убытков. Допустим, по рассматриваемым N договорам произошло М стра-ховых случаев, и выплаты составили SB1,… , SBj , … , SBM (всего М страховых случаев). Тогда наблюдаемая частота страховых случаев может быть рассчитана как отношение количества убытков к общему числу договоров: q = 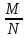 Строго говоря, данный показатель может быть как меньше единицы, так и больше нее. Последнее имеет место, если данный вид страхования пре-дусматривает возможность наступления нескольких случаев в течение срока страхования и вероятность этих случаев достаточно велика. Например, в добровольном медицинском страховании в качестве страхового случая может рассматриваться каждое посещение врача или отдельная процедура. Однако в большинстве видов страхования это отношение существенно меньше еди-ницы. Для определения относительной тяжести страховых случаев надо знать ожидаемые значения выплаты и страховой суммы. Из теории вероятностей и статистики известно, что среднее значение является состоятельной несме-щенной оценкой математического ожидания теоретического распределения. Поэтому в качестве оценок указанных параметров можно использовать средние значения выплаты и страховой суммы: Sв = 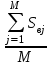 и S = и S = 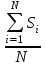 Отношение этих величин характеризует тяжесть страхового случая. В тех видах страхования, где предусмотрена выплата полной страховой суммы (как, например, в страховании на случай смерти), оно равно единице. В ос-тальных случаях – меньше ее. Если при расчете тарифов для нового стра-хового продукта отсутствует информация о фактических страховых суммах и убытках, данный показатель оценивается экспертным путем. Однако такие оценки носят весьма приблизительный характер и подлежат корректировке по мере накопления статистических данных. Используя полученные пара-метры, определяется основная часть нетто-ставки То: To = q* 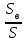 Для расчета рисковой надбавки по рекомендуемой в Методике фор-муле дополнительно необходимо задать требуемый уровень гарантии безо-пасности γ и планируемое количество договоров страхования n. Исходя из установленного уровня гарантии безопасности по таблице квантилей нор-мального распределения определяется коэффициент α (γ), и его значение под-ставляются в формулу Tp = 1,2 * α (γ) * To 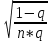 Нетто-ставка получается путем сложения основной части и рисковой надбавки: Tн = To + Tp Расчет брутто-ставки Тб осуществляется по общей формуле Tб = 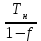 Здесь f – доля нагрузки в брутто-ставке, которая уже рассматривалась в предыдущем параграфе. Обычно она одинакова для всех тарификационных групп в рамках одного страхового продукта. Следуя изложенной методике, можно рассчитать базовые тарифные ставки для всех групп (категорий) рисков в тарификационной системе. Убыточность страховой суммы. Если подставить выражения для оце-нок параметров в формулу расчета основной части нетто-ставки, то можно увидеть, что она равна отношению суммы выплат к совокупной страховой сумме: To = q * 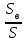 = = 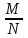 * * 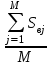 * * 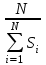 = = 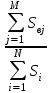 B страховании данное отношение называется «убыточность стра-ховой суммы» и считается одним из важнейших индикаторов, который по-казывает среднюю величину выплат с единицы страховой суммы. Поскольку убыточность является относительным показателем, она слабо зависит от фактических значений сумм выплат и страховых сумм и достаточно объ-ективно характеризует опасность, «рисковость» данного вида страхования или отдельного страхового продукта. Чем выше убыточность, тем больше ожидаемый убыток с каждого договора и тем дороже страхование. Поэтому данный показатель, рассчитанный по статистике за прошлые периоды, яв-ляется хорошим ориентиром для определения тарифов в будущем. В отечественной практике «убыточностью» также часто называют дру-гой показатель, равный отношению выплат к премиям, полученным или заработанным в определенном периоде. Строго говоря, это отношение сле-довало бы называть «убыточность страховой премии», поскольку оно по-казывает, какая часть от каждого рубля страховой премии идет на выплаты. Данный показатель более субъективен, чем убыточность страховой суммы. Кроме характеристик самого риска и качества работы андеррайтеров по селекции на его величину сильно влияет правильность определения тарифов. Поэтому «убыточность страховой премии» в большей степени подходит для текущей оценки доходности страховых операций, чем для чистого техни-ческого анализа рисков. В западной практике этот показатель специального названия не имеет. |
