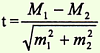Общественное здоровье и здравоохранение как наука и предмет преподавания. Показатели общественного здоровья и факторы его формирующие

• Название: Общественное здоровье и здравоохранение как наука и предмет преподавания. Показатели общественного здоровья и факторы его формирующие
• Дата: 01.02.2022
• Размер: 1.32 Mb.
• Имя файла: Metodichka.docx
• Тип: Документы; #348476
• страница: 2 из 21

§ каждая диаграмма должна иметь четкое, ясное, краткое название, отражающее ее содержание, и порядковый номер;

§ все элементы диаграммы (фигуры, знаки, окраска, штриховка) должны быть пояснены на самой диаграмме или в условных обозначениях (легенде);

§ изображаемые графически величины должны иметь цифровые обозначения на самой диаграмме или в прилагаемой таблице;

§ данные на диаграмме должны размещаться от большего к меньшему, слева направо, снизу вверх и по часовой стрелке (но элемент «прочие» всегда располагается последним).

Заканчивается данный этап формулировкой выводов и литературным оформлением полученного материала.

 

17. 
    Вариационные ряды, их виды, методика построения. Обобщенная числовая характеристика изучаемого признака в вариационном ряду.
    

Для расчета средней величины необходимо построить вариационный ряд — т. е. ряд числовых измерений определенного признака, отличающихся по своей величине.

Вариационные ряды бывают следующих видов:

а) ранжированный, неранжированный;

б) сгруппированный, несгруппированный;

в) прерывный, непрерывный.

Ранжированный ряд — упорядоченный ряд; варианты располагаются последовательно по нарастанию или убыванию числовых значений.

Неранжированный ряд — варианты располагаются бессистемно.

Прерывный (дискретный) ряд — варианты выражены в виде целых (дискретных) чисел (окна в избе).

Непрерывный ряд – варианты могут быть выражены дробными числами.

Несгруппированный ряд – каждому значению варианты соответствует определенное число частот.

Сгруппированный ряд (интервальный) – варианты соединены в группы, объединяющие их по величине в пределах определенного интервала.

Ряд, в котором упорядоченно сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты, называется вариационным. Отдельные числовые значения признака называются вариантами (У), а числа, показывающие, как часто эти варианты повторяются - частотами (Р), общее число наблюдений (n) равно сумме частот. Вариационный ряд может быть простым или сгруппированным. Простой вариационный ряд составляется при малом числе наблюдений (n<30), а сгруппированный - при большом числе наблюдений (n>30). Построение вариационного ряда из отдельных вариант - это только первый шаг к осмыслению особенностей всей совокупности. Далее для обобщенной числовой характеристики изучаемого признака у совокупности обследуемых рассчитываются средние величины, достоинство которых заключаются в том, что одна величина характеризует большую совокупность однородных явлений.

18. 
    Средние величины, их виды. Методика вычисления и применение при изучении состояния здоровья врачами общей практики.
    

Средние величины дают обобщающую характеристику статистической совокупности по определенному изменяющемуся количественному признаку.

Средняя величина характеризует весь ряд наблюдений одним числом, выражающим общую меру изучаемого признака. Она нивелирует случайные отклонения отдельных наблюдений и дает типичную характеристику количест­венного признака.

В медицинской практике наиболее часто используются следующие сред­ние величины: мода, медиана, средняя арифметическая. Реже применяются другие средние величины: средняя геометрическая (при обработке результатов титрования антител, токсинов, вакцин); средняя квадратическая (при определе­нии среднего диаметра среза клеток, результатов накожных иммунологических проб); средняя кубическая (для определения среднего объема опухолей), сред­няя прогрессивная и др.

Мода (Мо) — величина признака, чаще других встречающаяся в сово­купности. За моду принимают варианту, которой соответствует наибольшее ко­личество частот вариационного ряда.

Медиана(Me) — величина признака, занимающая срединное положение в вариационном ряду. Она делит вариационный ряд на две равные части. Для определения медианы следует найти ее порядковый номер в вариационном ря­ду по формуле, а затем установить ее числовое значение:

Порядковый номер медианы четного ряда = n/2

Порядковый номер медианы нечетного ряда =(n+1)/2

Зная порядковый номер медианы в вариационном ряду, определяют ее числовое значение.

На величину моды и медианы не оказывают влияния числовые значения крайних вариант, имеющихся в вариационном ряду. Мода и медиана применя­ются в медицинской статистике относительно редко. Более точно характеризует вариационный ряд средняя арифметическая величина, которая чаще других средних величин используется в медицинской статистике.

Средняя арифметическая(М,илиX) — рассчитывается на основе всех числовых значений изучаемого признака.

В простом вариационном ряду, где варианты встречаются только по од­ному разу, вычисляется средняя арифметическая простая по формуле:

М(Х) =

где V — числовые значения вариант, п — число наблюдений.

В обычном вариационном ряду вычисляется средняя арифметическая взвешенная по формуле:

М(Х) =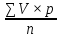

где V — числовые значения вариант, р — частота встречаемости вариант, п — число наблюдений.

Средняя величина — именованная величина, она выражается в тех же единицах измерения, что и варианта (днях, килограммах, метрах и т. д.)

Средние величины являются важными обобщающими характеристиками совокупности. Однако за ними скрываются индивидуальные значения признака. Средние величины не показывают изменчивости, колеблемости признака.

Если вариационный ряд более компактен, менее рассеян и все отдельные значения расположены вокруг средней, то средняя величина дает более точную характеристику данной совокупности. Если вариационный ряд растянут, от­дельные значения значительно отклоняются от средней, т. е. имеется большая вариабельность количественного признака, то средняя менее типична, недоста­точно точно отражает в целом весь ряд.

Одинаковые по величине средние могут быть получены из рядов с раз­личной степенью рассеяния.

Средние величины широко применяются в повседневной работе меди­цинских работников, в частности:

1) для характеристики физического развития: рост, вес, окружность груди, динамометрия и т. д.;

2) оценки состояния здоровья человека путем анализа физиологиче­ских, биохимических параметров организма (уровня артериального давле­ния, частоты сердечных сокращений, температуры тела уровня биохимических показателей, содержания гормонов и т. д.);

3) анализа деятельности медицинских организаций, например:

+— при анализе работы стационаров вычисляются показатели: среднее число дней работы койки в году, средняя длительность пребывания больного на койке и т. д.;

— при оценке работы амбулаторно-поликлинических организаций — сред­нее число посещений на одного жителя в год, средняя продолжительность одного случая заболеваемости с временной утратой трудоспособности и т. д.;

4) для оценки работы врачей: рассчитываются среднее число посещений на одного врача среднее число хирургических операций, среднечасовая нагрузка врача на приеме в поликлинике, среднее число лабораторных исследований и т. д.

19. Средняя ошибка средней арифметической и относительного показателя, методика вычисления. Значение при оценке достоверности результатов исследования.

Полученные в результате статистического исследования средние и относительные величины должны отражать закономерности, характерные для всей совокупности. Результаты исследования обычно тем достовернее, чем больше сделано наблюдений, и наиболее точными они являются при сплошном исследовании (т.е. при изучении генеральной совокупности). Однако должны быть достаточно надежные и данные, полученные путем выборочных исследований, т.е. на относительно небольшом числе наблюдений.

Различие результатов выборочного исследования и результатов, которые могут быть получены на генеральной совокупности, представляет собой ошибку выборочного исследования, которую можно точно определить математическим путем. Метод ее оценки основан на закономерностях случайных вариаций, установленных теорией вероятности.

1. Оценка достоверности средней арифметической.

Средняя арифметическая, полученная при обработке результатов научно-практических исследований, под влиянием случайных явлений может отличаться от средних, полученных при проведении повторных исследований. Поэтому, чтобы иметь представление о возможных пределах колебаний средней, о том, с какой вероятностью возможно перенести результаты исследования с выборочной совокупности на всю генеральную совокупность, определяют степень достоверности средней величины.

Мерой достоверности средней является средняя ошибка средней арифметической (ошибка репрезентативности – m). Ошибки репрезентативности возникают в связи с тем, что при выборочным наблюдении изучается только часть генеральной совокупности, которая недостаточно точно ее представляет.Фактически ошибка репрезентативности является разностью между средними, полученными при выборочном статистическом наблюдении, и средними, которые были бы получены при сплошном наблюдении (т.е. при изучении всей генеральной совокупности).

Средняя ошибка средней арифметической вычисляется по формуле:

- при числе наблюдений больше 30 (n > 30):

- при небольшом числе наблюдений (n < 30):

Ошибка репрезентативности прямо пропорциональна колеблемости ряда (сигме) и обратно пропорциональна числу наблюдений.

Следовательно, чем больше число наблюдений (т.е. чем ближе по числу наблюдений выборочная совокупность к генеральной), тем меньше ошибка репрезентативности.

Интервал, в котором с заданным уровнем вероятности колеблется истинное значение средней величины или показателя, называется доверительным интервалом, а его границы – доверительными границами. Они используются для определения размеров средней или показателя в генеральной совокупности.

Доверительные границы средней арифметической и показателя в генеральной совокупности равны:

M + tm

P + tm,

где t – доверительный коэффициент.

Доверительный коэффициент (t) – это число, показывающее, во сколько раз надо увеличить ошибку средней величины или показателя, чтобы при данном числе наблюдений с желаемой степенью вероятности утверждать, что они не выйдут за полученные таким образом пределы.

С увеличением t степень вероятности возрастает.

Т.к. известно, что полученная средняя или показатель при повторных наблюдениях, даже при одинаковых условиях, в силу случайных колебаний будут отличаться от предыдущего результат, теорией статистики установлена степень вероятности, с которой можно ожидать, что колебания эти не выйдут за определенные пределы. Так, колебания средней в интервале M + 1m гарантируют ее точность с вероятностью 68.3% (такая степень вероятности не удовлетворяет исследователей), в интервале M + 2m – 95.5% (достаточная степень вероятности) и в интервале M + 3m – 99,7% (большая степень вероятности).

Для медико-биологических исследований принята степень вероятности 95% (t = 2), что соответствует доверительному интервалу M + 2m.

Это означает, что практически с полной достоверностью (в 95%) можно утверждать, что полученный средний результат (М) отклоняется от истинного значения не больше, чем на удвоенную (M + 2m) ошибку.

Конечный результат любого медико-статистического исследования выражается средней арифметической и ее параметрами:



2. Оценка достоверности относительных величин (показателей).

Средняя ошибка показателя также служит для определения пределов его случайных колебаний, т.е. дает представление, в каких пределах может находиться показатель в различных выборках в зависимости от случайных причин. С увеличением численности выборки ошибка уменьшается.

Мерой достоверности показателя является его средняя ошибка (m), которая показывает, на сколько результат, полученный при выборочным исследовании, отличается от результата, который был бы получен при изучении всей генеральной совокупности.

Средняя ошибка показателя определяется по формуле:



где mp – ошибка относительного показателя,

р – показатель,

q – величина, обратная показателю (100-p, 1000-р и т.д. в зависимости от того, на какое основание рассчитан показатель);

n – число наблюдений.

20. Методика оценки достоверности средних и относительных величин.

При анализе многих явлений (рождаемости, смертности, заболеваемости и т.д.), измеряемых при помощи статистических показателей, часто возникает вопрос о том, в какой мере выводы, полученные при данном числе наблюдений, могут считаться значимыми, надежными, т.е. можно ли распространить эти выводы на всю массу аналогичных явлений. Так, например, можно ли считать, что препарат, оказавшийся эффективным при лечении пневмонии у данной группы больных, при прочих равных условиях даст положительный эффект и при лечении всех других больных пневмонией?

Подобного рода вопросы могут встать перед врачом при оценке различных методов лечения, успешности каких-либо хирургических вмешательств, при оценке здоровья населения и эффективности лечебно-профилактических мероприятий.

Значимость, надежность показателя (то же самое существенность, неслучайность), т.е. право показателя на обобщающую характеристику явления называется статистической достоверностью.

При правильно организованном статистическом наблюдении и правильной группировке собранных в процессе наблюдения материалов результаты исследования обычно тем достовернее, чем больше сделано наблюдений (первое положение закона «больших чисел»). Это не значит, однако, что следует стремиться бесконечно увеличивать число наблюдений. Иногда это увеличение практически неосуществимо, а иногда и не нужно, так как при наличии относительно небольшого, но однородного статистического материала можно быть уверенным в надежности выводов. Следовательно, достаточно ограничиться таким объемом, который дает устойчивые значимые результаты (второе положение закона «больших чисел»), т. е. такой выборочной совокупностью, в которой проявляются основные закономерности всей генеральной совокупности в целом.

При этом следует помнить, что статистические показатели, рассчитанные из выборочной совокупности, всегда имеют среднюю ошибку (ошибка выборки), т. е. пределы колебаний показателя в зависимости от случайных причин.

По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генеральной совокупности.

Каждая средняя величина - М (средняя длительность лечения, средний рост, средняя масса тела, средний уровень белка крови и др.), а также каждая относительная величина - Р (уровень летальности, заболеваемости и др.) должны быть представлены со своей средней ошибкой - m.

Средняя ошибка (m) для относительных показателей (Р) определяется по формуле: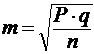



где Р - величина показателя;

q = 1 - Р если показатель выражен в долях единицы;

q = 100 - Р если показатель выражен в процентах;

q = 1000 - Р если показатель выражен в промилях;

n - число наблюдений.

Средняя ошибка (m) для средних величин (М) рассчитывается по формуле:



где сигма - среднее квадратическое отклонение;

n - число наблюдений.

При вычислении средних ошибок в условиях малой выборки (число наблюдений меньше 30) в знаменателе формул следует брать n, уменьшенное на 1.

21. Оценка достоверности разности средних и относительных показателей. Методика вычисления и применение в практической деятельности врача.

Данный способ применяется в тех случаях, когда необходимо определить, случайны или достоверны (существенны), т.е. обусловлены какой-то причиной, различия между двумя средними величинами или относительными показателями.

+Обязательным условием для применения данного способа является репрезентативность выборочных совокупностей, а также наличие причинно-следственной связи между сравниваемыми величинами (показателями) и факторами, влияющими на них.

Формулы определения достоверности разности представлены следующим образом:

для средних величин

для относительных показателей

где t - критерий достоверности, m1 и m2 - ошибки репрезентативности, М1 и М2 - средние величины, Р1 и Р2 - относительные показатели.

Если вычисленный критерий t более или равен 2 (t ≥ 2), что соответствует вероятности безошибочного прогноза Р равном или более 95% (Р ≥ 95%), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности.

При t < 2, вероятность безошибочного прогноза Р< 95%, это означает, что разность недостоверна, случайна, т.е. не обусловлена какой-то закономерностью (не обусловлена влиянием какого-то фактора).

Поэтому полученный критерий должен всегда оцениваться по отношению к конкретной цели исследования.

22. Методика определения доверительных границ средних и относительных показателей. Значение для практического здравоохранения.

Определяя для средней арифметической (или относительной) величины два крайних значения: минимально возможное и максимально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами.

Доверительные границы - границы средних (или относительных) величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность.

Вероятность попадания средней или относительной величины в доверительный интервал называется доверительной вероятностью.

Формулы определения доверительных границ представлены следующим образом:

·для средних величин (М): Мген=Мвыб ± tm

· для относительных показателей (Р): Рген=Рвыб ± tm

где Мген и Рген - соответственно, значения средней величины и относительного показателя генеральной совокупности;

Мвыб и Рвыб – значения средней величины и относительного показателя выборочной совокупности;

m- ошибка репрезентативности;

t- критерий достоверности (доверительный коэффициент).

Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности.

Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов, полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р), показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в генеральной совокупности.

При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам задает определенную (необходимую) степень вероятности безошибочного прогноза (Р).

Для большинства медико-биологических исследований считается достаточной степень вероятности безошибочного прогноза, равная 95 %, а число случаев генеральной совокупности, в котором могут наблюдаться отклонения от закономерностей, установленных при выборочном исследовании, не будут превышать 5%. При ряде исследований, связанных , например, с применением высокотоксичных веществ, вакцин, оперативного лечения и т.п., в результате чего возможны тяжелые заболевания, осложнения, летальные исходы, применяется степень вероятности Р=99,7 %, т.е. не более чем у 1% случаев генеральной совокупности возможны отклонения от закономерностей , установленных в выборочной совокупности.

Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t, зависящее также и от числа наблюдений.

При n>30 степени вероятности безошибочного прогноза Р=99,7% -- соответствует значение t= 3, а при Р=95,5 % - значение t=2.

При n<30 величина t при соответствующей степени вероятности безошибочного прогноза определяется по специальной таблице (Н.А. Плохинского).

23. Корреляция. Методика вычисления и использование в практической деятельности врачаобщей практики.

Корреляционные – это такие связи, когда при одном и том же значении факторного признака значения результативного признака различны, однако изменение факторного признака вызывает средние изменения результативного признака

При корреляционной связи одной и той же величине одного признака соответствуют разные величины другого. Например: между ростом и весом имеется корреляционная связь, между заболеваемостью злокачественныминовообразованиямии возрастом и т.д.

+Существует 2 метода вычисления коэффициента корреляции: метод квадратов( Пирсона), метод рангов (Спирмена).

Наиболее точным является метод квадратов (Пирсона), при котором коэффициент корреляции определяется по формул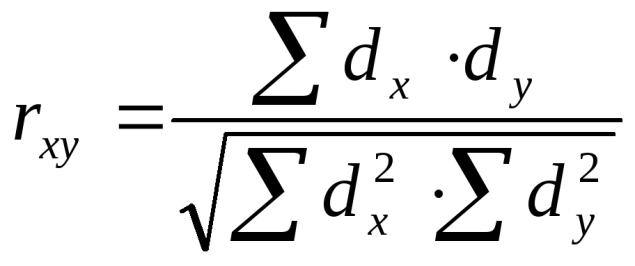е:

, где

rху ― коэффициент корреляции между статистическим рядом X и Y.

dх ― отклонение каждого из чисел статистического ряда X от своей средней арифметической.

dу ― отклонение каждого из чисел статистического ряда Y от своей средней арифметической.

В зависимости от силы связи и ее направления коэффициент корреляции может находиться в пределах от 0 до 1 (-1). Коэффициент корреляции, равный 0, говорит о полном отсутствии связи. Чем ближе уровень коэффициента корреляции к 1 или (-1), тем соответственно больше, теснее измеряемая им прямая или обратная связь. При коэффициенте корреляции равном 1 или (-1) связь полная, функциональная.

Коэффициент корреляции можно определить несколько менее точным, но намного более легким способом ― методом рангов (Спирмена).

МетодСпирмена: P=1-(6∑d2/n-(n2-1))

-составить два ряда из парных сопоставляемых признаков, обозначив первый и второй ряд соответственно х и у. При этом представить первый ряд признака в убывающем или возрастающем порядке, а числовые значения второго ряда расположить напротив тех значений первого ряда, которым они соответствуют

-величину признака в каждом из сравниваемых рядов заменить порядковым номером (рангом). Рангами, или номерами, обозначают места показателей (значения) первого и второго рядов. При этом числовым значениям второго признака ранги должны присваиваться в том же порядке, какой был принят при раздаче их величинам первого признака. При одинаковых величинах признака в ряду ранги следует определять как среднее число из суммы порядковых номеров этих величин

-определить разность рангов между х и у (d): d = х — у

-возвести полученную разность рангов в квадрат (d2)

-получить сумму квадратов разности (Σ d2) и подставить полученные значения в формулу.

24. Динамические ряды и их анализ в практической деятельности врача общей практики.

Динамический ряд — это ряд однородных статистических величин, показывающих изменение явления во времени. Динамический ряд может быть представлен абсолютными числами (изменение числа больных), средними величинами (среднее число лабораторных анализов за неделю) и относительными показателями (изменение рождаемости, заболеваемости, травматизма, обеспеченности врачами). Числа, из которых состоит динамический ряд, называются уровнями ряда. Анализ динамического (временного) ряда сводится к вычислению следующих показателей: абсолютного прироста (или снижения); темпа роста (или снижения); темпа прироста; значения 1% прироста.

Абсолютныйприростпредставляет собой разность между последующим и предыдущим уровнем.

Темп роста — это отношение последующего уровня к предыдущему, умноженное на 100%.

Темп прироста является отношением абсолютного прироста (снижения) к предыдущему уровню, умноженным на 100%.

Значение 1% прироста определяется отношением абсолютного прироста к темпу прироста.

25. Стандартизированные показатели. Методика вычисления и использование в работе врача общей практики.

При изучении общественного здоровья и здравоохранения в научных или практических целях исследователю нередко приходится доказывать влияние факторных признаков на результативные при сравнении двух или более совокупностей. С этой целью применяется целый ряд статистических приемов.

Стандартизация – метод расчета условных (стандартизированных) показателей, замещающих интенсивные показатели в тех случаях, когда сравнение последних недопустимо из – за несоответствия сравниваемых групп.

-Прямой метод – наличие полных сведений как о составе сравниваемых совокупностей, так и распределении в них явлений.

-Косвенный метод – известен состав среды, но неизвестен состав явления или оно выражено малыми цифрами.

-Обратный косвенному – известен состав явления, но неизвестен состав среды.

Сущность: устраняет возможное влияние различий в составе совокупностей по какому – либо признаку на величину сравниваемых интенсивных показателей. Применяется для выявление влияния фактора неоднородности составов совокупностей по какому – либо признаку на величину сравниваемых интенсивных показателей.

Стандартизированные показатели - условные, гипотетические показатели, они не отражают истинные размеры явлений.

Этапы расчета прямого метода стандартизации:

I этап. Расчет общих и частных интенсивных показателей:

-общих — по совокупностям в целом;

-частных — по признаку различия (полу, возрасту, стажу работы и т.д.).

II этап. Определение стандарта, т.е. выбор одинакового численного состава среды по данному признаку (по возрасту, полу и т.д.) для сравниваемых совокупностей. Как правило, за стандарт принимается сумма или полусумма численностей составов соответствующих групп. В то же время стандартом может стать состав любой из сравниваемых совокупностей, а также состав по аналогичному признаку какой-либо другой совокупности. Например, при сравнении летальности в конкретной больнице по двум отделениям скорой помощи за стандарт может быть выбран состав больных любой другой больницы скорой помощи. Таким образом, так или иначе уравниваются условия среды, что дает возможность провести расчеты новых чисел явления, называемых "ожидаемыми величинами".

III этап. Вычисление ожидаемых абсолютных величин в группах стандарта на основе групповых интенсивных показателей, рассчитанных на I этапе. Итоговые числа по сравниваемым совокупностям являются суммой ожидаемых величин в группах.

IV этап. Вычисление стандартизованных показателей для сравниваемых совокупностей.

V этап. Сопоставление соотношений стандартизованных и интенсивных показателей, формулировка вывода.

26. Медицинская демография как наука, ее основные разделы, значение для оценки здоровья населения.

Демография – это наука о закономерностях воспроизводства населения, о зависимости его характера от социально-экономических, природных условий, миграции, изучающая численность, территориальное размещение и состав населения, их изменения, причины и следствия этих изменений и дающая рекомендации по их улучшению.

Демографией иногда называют вид практической деятельности по сбору данных, описанию и анализу изменений в численности, составе и воспроизводстве населения.

Демографические исследования служат для разработки демографической политики, планирования трудовых ресурсов и пр.

В соответствии с планом мероприятий по реализации концепции демографической политики проводят специальные мероприятия по снижению смертности населения от ссс заболеваний. Дорожно -транспортных проишествий, производственного травматизма, по повышению рождаемости, качества медико-социальной помощи, женщинам и детям, обеспечению доступности высокотехнологичесокоймедицинсок помощи , профилактике заболеваний и укреплению основ здорового образа жизни, по развитию социальной поддержке семьи, содействию занятости граждан.

Можно выделить четыре группы проблем, которые влечет за собой старение современного общества.

Во-первых, это демографические и макроэкономические последствия, которые затронут такие характеристики, как:

- показатель рождаемости:

- продолжительность жизни, и особенно верхние пределы долгожительства, а также количество пожилых людей, которые хотели бы достичь их;

- распределение материальных ресурсов между представителями различных поколений;

- отношение к коллективной ответственности за обеспечение соответствующих стандартов и качество жизни пожилых людей-пенсионеров;

- уровень производительности труда.

Во-вторых, будет затронута сфера социальных отношений, произойдут существенные изменения:

-в структуре семейно-родственных отношений;

- в системе поддержки друг друга разных поколений;

- в характере выбора будущей профессии;

- в структуре потенциальной занятости.

В-третьих, изменение демографической структуры отразится на рынке труда, и в частности:

- изменится соотношение между умственным и физическим трудом и отношение общества к трудовой деятельности;

- возникнет необходимость переквалификации трудящихся в пожилом возрасте;

В-четвертых, изменения коснутся функциональных способностей и состояния здоровья пожилых людей, что повлечет за собой серьезные последствия для социальных служб.

27. Основные закономерности естественного движения населения в России и других странах мира. Современные проблемы воспроизводства населения.

Естественное движение населения — это совокупность таких демографических явлений, как рождаемость, смертность, естественный прирост населения, младенческая смертность, данные о браках, разводах, средней продолжительности предстоящей жизни, регистрация которых производится в медицинских учреждениях и органах записи актов гражданского состояния. Статистика естественного движения населения основана на обязательной регистрации рождений, смертей, браков, разводов по специальным документам (справки о рождении, свидетельства о смерти, акты о записи).

Урбанизация — это демографический процесс, который характеризуется ростом числа городов, увеличением их мощности и вследствие этого преобладанием доли городских жителей среди всего населения. В России доля городского населения увеличилась с 18% в 1897 г. до 67% в 1989 г. (по данным последней переписи). В перспективе городские жители будут составлять 80% от всего населения страны.

28 .Динамика населения, ее виды. Миграция населения: внешняя, внутренняя. Факторы, ее определяющие; основные тенденции. Влияние миграции на здоровье населения; задачи органов и учреждений здравоохранения.

Миграция - это перемещение людей связанное, как правило, со сменой места жительства.

Виды миграции:

· Безвозвратная миграция – пост. смена постоянного места жительства. Временная миграция это переселение на достат. длительный, но огранич. срок.

· Сезонная миграция – перемещ. в опред. времена годы, как правило, летом.

· Маятниковая миграция – регул. поездки к месту работы или учебы из другого нас. пункта.

Миграция также бывает:

· Внешняя это миграция за пределы своей страны. К ней отн. эмиграция и иммиграция.

· Внутренняя: межрайоные перемещения, пересел. из села в город.

За последние 5 лет численность сельского населения увеличилась на 2%. Это говорит о том что процесс урбанизации замедляется.

Значение миграционных процессов: Урбанизация изменяет экологическую обстановку. Изменяется структура заболеваемости и смертности населения. Процесс урбанизации требует пересмотра нормативов мед. помощи, изменения сети мед. учреждений. Процесс урбанизации ведет к росту внебрачной рождаемости. Маятниковая миграция способствует распространению инфекционных заболеваний, ведет к росту стрессовых ситуаций, травматизму. Сезонная миграция ведет к неравномерной сезонной нагрузке на мед. учреждения, влияет на показатели здоровья населения. Показатели здоровья мигрантов существенно отличаются от показателей здоровья коренного населения.

29. Статика населения. Методика изучения и основные данные по России и странам мира. Значение для здравоохранения.

Статика населения - численный состав населения на определенный момент времени, изучается по ряду основных признаков: пол, возраст, социальные группы, профессия, семейное положение, национальность, язык, культурный уровень, религия, место жительства, географическое размещение, плотность населения и т.д.

Наиболее важными показателями, характеризующими статику населения, являются:

· Структура населения по возрасту (тип возрастной структуры населения)

· численность постоянного и фактического населения

· плотность населения.

Основные черты современных переписей населения:

· всеобщность,

· единство программы,

· поименность регистрации,

· одновременность регистрации на определенный момент переписи,

· сбор информации непосредственно у населения,

· сведения собираются методом интервьюирования (путем личной беседы с каждым человеком).

Значение статики для практического здравоохранения: показатели статики населения необходимы для:

· расчета показателей естественного движения населения;

· расчета показателей общественного здоровья населения;

· планирования и организации видов медицинской помощи населению

· определения финансовых средств, выделяемых из государственного бюджета на здравоохранение;

· организации противоэпидемической работы в регионе;

· расчета показателей, характеризующих деятельность органов и учреждений здравоохранения, врачей;

· расчета потребности населения в медицинских кадрах

30.Переписи населения как источник информации о статике населения, история, методика проведения, результаты.

Перепись населения является одной из наиболее крупных и сложных статистических работ. Выполнение ее связано с решением многих методологических и организационных вопросов, привлечением значительного числа переписного персонала. Одним из важнейших условий качественной подготовки и проведения переписи является обеспечение высокого уровня массово-разъяснительной работы среди населения. Опыт прошлых переписей показывает, что от того, насколько активно ведется эта работа, зависит знание населением задач переписи и его отношение к ней, содействие переписному персоналу, правильность ответов на вопросы переписного листа.

Методы проведения переписи:

· Опрос — при этом методе проведения переписи переписной лист заполняется переписчиком (счётчиком, регистратором) в процессе личной беседы с переписываемым лицом. По этому методу проводились переписи населения России и СССР;

· Самоисчисление — переписываемые сами заполняют переписной лист, а переписчик (счётчик, регистратор) лишь проверяет правильность его заполнения, уточняя пропущенные или неясные сведения. Применяется в некоторых европейских странах;

· Смешанный (анкетный) метод (активно применяется за рубежом, в том числе в США) — при этом методе анкеты рассылаются переписчикам, которые сами заполняют их и затем высылают в бюро переписей или статистическую службу. По окончании сбора заполненных анкет статслужба (бюро переписей) проводят их сверку и направляют переписчикам по тем адресам, откуда не получены анкеты, для проведения опроса жителей. Обычно материальные затраты на проведения переписи таким методом менее велики, чем при опросе, однако степень возврата заполненных анкет остается невелика (около 15-20 %), даже с учётом значительных затрат на пропаганду переписи.

31 . Перепись населения, её значение для органов здравоохранения. Основные итоги всероссийской переписи населения 2010 года.

На основании расчета удельного веса лиц в возрасте 0-14 лет, 15-49 лет, 50 лет и старше определили тип возрастной структуры населения.

Согласно первым предварительным результатам, оглашённым в ноябре 2010 года, в России было переписано около 141,18 млн человек. Россия перешла по численности населения с 7 на 8 место в мире.

32. Рождаемость. Методы изучения, общие и специальные показатели. Факторы, влияющие на уровень рождаемости.

Рождаемость — процесс возобновления новых поколении, в основе которого лежат биологические факторы, влияющие на способность организма к воспроизводству потомства (зачатие, оплодотворение, вынашивание плода).







Факторы, оказывающие влияние на рождаемость:

• обществен. положение женщин,

• их занятость в производстве,

• уровень удовлетворения их материальных потребностей,

• жилищные условия,

• степень обеспеченности,

• уровень детской смертности.

33. Смертность. Методика изучения, данные по России и странам мира. Основные причины смертности и их врачебная регистрация

Смертность - важнейший показатель естественного движения населения



Источником информации о причинах смерти в России являются записи во «Врачебных свидетельствах о смерти» или « Фельдшерских справках о смерти», заполняемых врачом (фельдшером).

34.Смертность населения, методика изучения, общие и повозрастные показатели. Факторы, влияющие на показатели смертности.

Смертность населения - массовый процесс прекращения индивидуальных жизней, протекающий в населении. Наряду с рождаемостью смертность формирует естественное движение (воспроизводство) населения.

Смертность зависит от большого числа природных и социальных факторов, которые можно разделить на две группы: эндогенные и экзогенные. Первые порождены внутренним развитием человеческого организма, и прежде всего его старением, вторые — связаны с воздействием внешней среды.

35. Младенческая смертность. Методика изучения, уровень, причины, пути снижения. Динамика уровня младенческой смертности в России и странах мира.



Структура причин младенческой смертности:

• состояния перинатального периода 34,2%,

• врожденные аномалии 27%,

• травмы, несчастные случаи, отравления 11,2%,

• инфекции 5,5%,

• болезни органов дыхания 5%.

Высокая младенческая смертность является признаком низкого уровня развития медицины и особо часто встречается в странах Третьего мира.

36. Перинатальная и неонатальная смертность. Методика изучения, уровень, основные причины, пути снижения.

Перинатальная смертность, т.е. потеря детей в перинатальный период – это количество мертворожденных (смерть наступила до родов или в родах) и раннюю неонатальную смертность (смерть наступила в течении 168 часов после рождения).

Формула:

Число мертворожденных + число детей, умерших в первые 168 часов * 1000 / число родившихся детей (живых и мертвых).

Неонатальная смертность:

Формула:

число детей умерших от 0 до 28 дней X 1000/ число родившихся живыми

пути снижения младенческой смертности:

• реализация комплексных региональных программ по снижению МС для территорий с высоким, средним и сравнительно низким ее уровнем;

• пренатальная диагностика патологии плода;

• внедрение ультразвукового пренатального скрининга;

• внедрение неонатального скрининга;

• диагностика внутриутробных инфекций;

• расширение Национального календаря вакцинации за счет включения новых эффективных и безопасных иммунобиологических препаратов;

• планирование семьи, внедрение современных контрацептивов;

• развитие и внедрение на всех этапах реанимации и интенсивной терапии новорожденных, широкое использование сурфактантов;

• изменение организационной структуры работы акушерских стационаров, их интеграции в структуру

• больничных комплексов; создание учреждений нового типа — перинатальных центров.

37. Смертность в трудоспособном возрасте, её уровень, динамика и основные причины. Система мер медицинского и немедицинского характера, направленная на снижение преждевременной смертности.

Проблема высокой смертности в трудоспособном возрасте (мужчины 16-59 лет, женщины 16-54 года) сохраняет свою остроту в России, несмотря на тенденцию снижения, сложившуюся в 2006-2017 годах.

Самое высокое значение коэффициента смертности в трудоспособном возрасте – 8,3 умерших в трудоспособном возрасте на 1000 человек трудоспособного возраста – зафиксировано в 2005 году. В 2003-2004 годах, а также в 1995 году значение коэффициента было немного меньше – 8,1 на 1000 человек. В эти годы доля людей трудоспособного возраста среди всех умерших превышала 30%, а в 2005 году она превысила 32%.



Меры по снижению смертности:

• 
  уменьшению влияния вредных факторов на организм человека
  
• 
  Формирование парадигмы здорового образа жизни
  
• 
  Меры по предупреждению соматических и психических заболеваний и травм
  
• 
  Проведение иммунопрофилактики (вакцинации) различных групп населения
  
• 
  Осуществление медицинского скрининга с целью снижения влияния факторов риска и раннего выявления
  
• 
  Диспансеризация населения с целью выявления рисков развития хронических соматических заболеваний
  

38. Проблема старения населения. Ее социальные, экономические и медицинские аспекты. Влияние постарения населения на организацию медицинской помощи.

Демографическое старение населения — увеличение доли пожилых людей в общей численности населения. Это результат длительных демографических изменений, сдвигов в характере воспроизводства населения, рождаемости, смертности, их соотношения, а также частично миграции.

Типы[

• 
  старение «снизу» (результат уменьшения рождаемости);
  
• 
  старение «сверху» (результат увеличения средней продолжительности жизни и снижения смертности в старших возрастах в условиях низкой рождаемости)
  

39. Особенности современной демографической ситуации в России, задачи органов здравоохранения по её оптимизации.

В широком смысле демографическая политика — это политика в области народонаселения. Объектом может выступать население страны, отдельных её районов, когорты населения, семьи определённых типов. Историческая цель демографической политики государства достижение демографического оптимума.

экономические

оплачиваемые отпуска; различные пособия при рождении ребёнка, часто в зависимости от их количества возраст и состояние семьи оцениваются по прогрессивной шкале ссуды, кредиты, налоговые и жилищные льготы — для повышения рождаемости преимущества для малодетных семей — для понижения рождаемости

административно-правовые

законодательные акты, регулирующие возраст вступления в брак, разводимость, отношение к абортам и контрацепции, имущественное положение матери и детей при распаде брака, режим труда работающих женщин

морально-психологические

формирование общественного мнения, норм и стандартов демографического поведения

определение отношения к религиозным нормам, традициям и обычаям политика планирования семьи половое образование молодёжи.

40. Международная классификация болезней и проблем, связанных со здоровьем. Основные принципы её построения и значение в деятельности врача общей практики.

Международная классификация болезней (МКБ) является стандартной диагностической методикой эпидемиологии, организации здравоохранения и диагностики заболеваний. МКБ позволяет проводить анализ состояния здоровья населения, организовывать мониторинг заболеваемости и распространения болезней, разрабатывать классификации заболеваний и нарушений здоровья, зафиксированных в медицинских и гражданских документальных источниках (медицинские карты, свидетельства о смерти).