определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Сложение матриц и умножение матрицы на число, свойства этих операций.Определение 5. Две матрицы 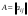 , , 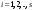 , , 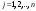 , и , и 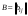 , , 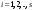 , , 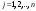 , будем называть равными, если , будем называть равными, если 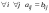 . .Определение 6. Суммой двух матриц 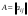 , , 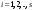 , , 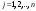 , и , и 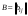 , , 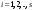 , , 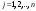 , называется такая матрица , называется такая матрица 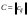 , , 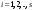 , , 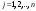 , что , что 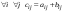 . .Определение 7. Произведением матрицы 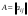 , , 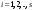 , , 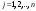 , на вещественное число , на вещественное число  называется такая матрица называется такая матрица 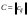 , , 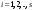 , , 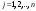 , для которой , для которой 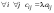 . .Свойства операций сложения матриц и умножения на число: 1. Сложение коммутативно: 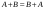 . .2. Сложение ассоциативно: 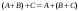 . .3. Существует нулевая матрица 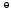 , удовлетворяющая условию , удовлетворяющая условию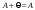 для всех А. для всех А.4. Для любой матрицы А существует противоположная матрица В, удовлетворяющая условию 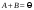 . .Для любых матриц А и В и любых действительных чисел 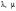 имеют место равенства: имеют место равенства:5. 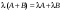 . .6. 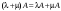 . .7. 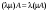 . .8. 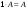 . . Умножение матриц, свойства умножения (доказать ассоциативность).Определение 8. Произведением матрицы 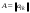 , , 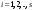 , , 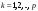 , на матрицу , на матрицу 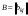 , , 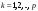 , , 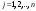 , называется матрица , называется матрица 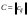 , , 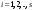 , , 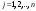 , с элементами , с элементами 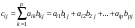 . .Замечание 1. Число элементов в строке матрицы  равно числу элементов в столбце матрицы равно числу элементов в столбце матрицы  (число столбцов матрицы (число столбцов матрицы  равно числу строк матрицы равно числу строк матрицы  ). ).Замечание 2. В матрице 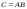 строк столько же, сколько в матрице строк столько же, сколько в матрице  , а столбцов столько же, сколько в , а столбцов столько же, сколько в  . .Замечание 3.Вообще говоря, 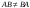 (умножение матриц некоммутативно). (умножение матриц некоммутативно).Чтобы обосновать замечание 3, достаточно привести хотя бы один пример. Свойства умножения матриц: Умножение дистрибутивно: 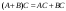 , , 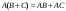 . .2. Умножение ассоциативно: 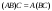 . .Теорема 2. Для любых двух квадратных матриц  и и  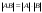 . . |
