определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Обратная матрица, существование и единственность.Утверждение 1. Матрица  - единственная матрица, обладающая свойством (7.1). - единственная матрица, обладающая свойством (7.1).Определение 1. Пусть  - произвольная квадратная матрица. Матрица - произвольная квадратная матрица. Матрица  называется правой обратной для называется правой обратной для  , если , если 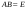 . Матрица . Матрица  называется левой обратной для называется левой обратной для  , если , если 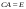 . .Определение 2. Квадратная матрица  называется вырожденной (особенной), если называется вырожденной (особенной), если 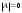 , и невырожденной (неособенной), если , и невырожденной (неособенной), если 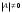 . .Утверждение 2. Вырожденная матрица не имеет ни правой, ни левой обратной. Утверждение 3.Пусть  - произвольный определитель порядка - произвольный определитель порядка  . Сумма произведений всех элементов любого столбца (строки) на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю. . Сумма произведений всех элементов любого столбца (строки) на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю.Утверждение 4. Матрица 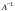 - единственная обратная для - единственная обратная для  . .Ранг матрицы. Теорема о базисном миноре.Определение 3. Пусть  - прямоугольная матрица размера - прямоугольная матрица размера 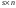 . Выберем в . Выберем в  произвольные произвольные 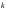 строк и строк и 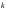 столбцов. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют определитель столбцов. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют определитель 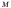 порядка порядка 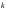 , который называется минором порядка , который называется минором порядка 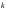 матрицы матрицы  . .Определение 4. Наивысший порядок отличных от нуля миноров матрицы  называется рангом матрицы называется рангом матрицы  . .Теорема 1 (о базисном миноре). Столбцы, содержащие базисный минор, линейно независимы. Любой столбец матрицы  является линейной комбинацией базисных столбцов одного и того же базисного минора. является линейной комбинацией базисных столбцов одного и того же базисного минора.Замечание.Аналогичное утверждение справедливо и для строк: строки, содержащие базисный минор, линейно независимы, через них линейно выражаются все остальные строки матрицы. Ранг матрицы. Вычисление ранга методом окаймляющих миноров.Теорема 2. Если в матрице  некоторый минор некоторый минор 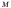 порядка порядка  отличен от нуля, а все окаймляющие его миноры равны нулю, то отличен от нуля, а все окаймляющие его миноры равны нулю, то 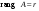 . . Метод элементарных преобразований Определение 5. Элементарными преобразованиями матрицы называются следующие: 1) перестановка двух строк (столбцов) матрицы; 2) умножение всех элементов строки (столбца) на вещественное число 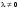 ; ;3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число. Теорема 3. Элементарные преобразования не изменяют ранга матрицы. Определение 6. Матрица  размером размером 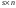 имеет диагональную форму, если имеет диагональную форму, если 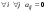 , кроме , кроме 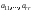 , , 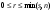 , т.е. , т.е.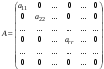 . .Утверждение. Всякую матрицу элементарными преобразованиями можно привести к диагональной форме. |
