определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Норма вектора. Неравенство Коши-Буняковского.Определение 2. Нормой вектора 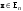 называется число, равное называется число, равное 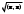 . .Теорема 1 (неравенство Коши - Буняковского). Для любого 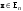 и любого и любого 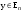 справедливо неравенство справедливо неравенство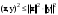 . (13.4) . (13.4)Линейная независимость системы ненулевых ортогональных векторов в евклидовом прос-стве.Определение 3. Пусть 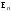 - евклидово пространство, - евклидово пространство, 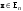 , , 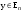 . Векторы . Векторы  и и  называются ортогональными, если называются ортогональными, если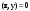 . .Определение 4. Система векторов 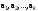 называется ортогональной системой векторов в евклидовом пространстве называется ортогональной системой векторов в евклидовом пространстве 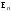 , если , если 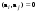 при при 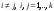 . .Справедливо следующее утверждение. Теорема 2. В евклидовом пространстве 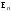 всякая система ненулевых ортогональных векторов линейно независима. всякая система ненулевых ортогональных векторов линейно независима.Процесс ортогонализации Шмидта.. Шаг 1. Примем 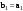 . .Шаг 2. Примем 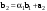 . . 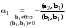 . .Шаг 3. Примем 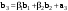 . . 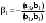 , , 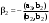 . .Шаг 4. Пусть уже построена ортогональная система ненулевых векторов 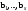 , причем , причем 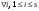 , , 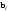 является линейной комбинацией векторов является линейной комбинацией векторов 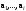 . Положим . Положим 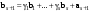 . .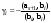 , , 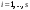 . .Ортогональные и ортонормированные базисы в евклидовом пространстве. Определение 5. Вектор 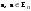 называется нормированным, если называется нормированным, если 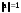 . . Определение 6. Система векторов 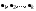 в евклидовом пространстве в евклидовом пространстве 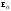 называется ортонормированной системой, если называется ортонормированной системой, если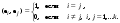 Теорема 3. Пусть 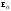 - евклидово пространство, - евклидово пространство, 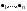 (I) – базис в (I) – базис в 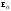 . Базис . Базис 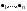 является ортонормированным тогда и только тогда, когда для любых векторов является ортонормированным тогда и только тогда, когда для любых векторов 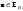 , , 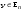 , , 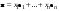 , , 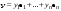 скалярное произведение выражается равенством скалярное произведение выражается равенством 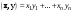 . . |
