определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Размерность линейного пространства.Определение 6. Число векторов в любом базисе линейного пространства  называется размерностью линейного пространства. называется размерностью линейного пространства.Для размерности линейного пространства  принято обозначение принято обозначение 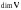 . .В рассмотренных примерах: если  - линейное пространство всех геометрических векторов пространства, - линейное пространство всех геометрических векторов пространства, 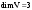 ; ;если  - линейное пространство всех многочленов степени - линейное пространство всех многочленов степени 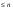 , , 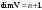 ; ;если  - линейное пространство всех квадратных матриц порядка 2, - линейное пространство всех квадратных матриц порядка 2, 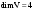 . .Связь между базисами линейного пространства.Определение 1. Матрица 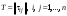 называется матрицей перехода от базиса (I) к базису (II). называется матрицей перехода от базиса (I) к базису (II).Замечание 1. Столбцы матрицы перехода 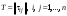 , являются координатами в разложении векторов , являются координатами в разложении векторов 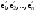 по базису (I). по базису (I).Замечание 2.Матрица перехода от базиса к базису является невырожденной матрицей. Теорема 1. Пусть  - линейное пространство, - линейное пространство, 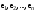 (I) и (I) и 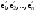 (II) - два базиса в (II) - два базиса в  , ,  - матрица перехода от (I) к (II), - матрица перехода от (I) к (II), 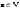 , , 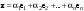 и и 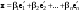 , тогда , тогда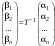 Линейные подпространства. Примеры.Определение 2. Пусть  - линейное пространство. Непустое подмножество - линейное пространство. Непустое подмножество  линейного пространства линейного пространства  ( (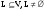 ) называется линейным подпространством в ) называется линейным подпространством в  , если выполняются два условия: , если выполняются два условия:1) 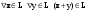 ; ;2) 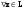 при любом вещественном числе при любом вещественном числе 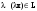 . .Замечание. Если  -линейное подпространство в -линейное подпространство в  , то , то  само является линейным пространством относительно введенных в само является линейным пространством относительно введенных в  операций сложения и умножения на число. операций сложения и умножения на число.Линейные операторы, определения и примеры.Определение 1. Пусть  - линейное пространство и каждому вектору - линейное пространство и каждому вектору  , принадлежащему , принадлежащему  , поставлен в соответствие вектор , поставлен в соответствие вектор  , , 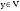 . Соответствие . Соответствие 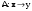 называется оператором, определенным в линейном пространстве называется оператором, определенным в линейном пространстве  . .Определение 2. Оператор  , определенный в линейном пространстве , определенный в линейном пространстве  , называется линейным, если: , называется линейным, если:1) 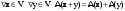 ; ;2) 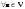 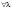 - вещественного числа - вещественного числа 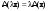 . . |
