определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Ортогональные матрицы, их свойства (доказать: Q является ортогональной тогда и только тогда, когда столбцы Q составляют ортонормированную систему).Определение 7. Квадратная матрица 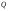 называется ортогональной, если называется ортогональной, если 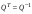 . .Утверждение 1. Квадратная матрица 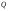 является ортогональной тогда и только тогда, когда ее столбцы составляют ортонормированную систему арифметических векторов. является ортогональной тогда и только тогда, когда ее столбцы составляют ортонормированную систему арифметических векторов. Ортогональные матрицы, их свойства (доказать: матрица перехода от ортонормированного базиса к ортонормированному базиса является ортогональной).Утверждение 2. Матрица перехода от ортонормированного базиса евклидова пространства к любому другому его ортонормированному базису является ортогональной. Ортогональные операторы в евклидовом пространстве, их свойства.Утверждение 2. Матрица перехода от ортонормированного базиса евклидова пространства к любому другому его ортонормированному базису является ортогональной. Теорема 2. В евклидовом пространстве 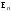 всякая система ненулевых ортогональных векторов линейно независима. всякая система ненулевых ортогональных векторов линейно независима.Определение 8. Линейный оператор  в евклидовом пространстве в евклидовом пространстве 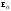 называется ортогональным, если называется ортогональным, если 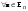 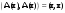 (оператор сохраняет норму любого вектора). Теорема 4. Пусть 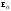 - евклидово пространство, - евклидово пространство,  - ортогональный оператор в - ортогональный оператор в 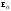 . Тогда . Тогда 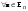 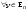 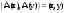 (  сохраняет скалярное произведение). сохраняет скалярное произведение).Теорема 5. Пусть 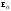 - евклидово пространство, - евклидово пространство, 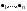 (I) - ортонормированный базис, (I) - ортонормированный базис,  - ортогональный оператор в - ортогональный оператор в 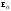 . Тогда система векторов . Тогда система векторов 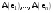 (II) - ортонормированный базис. (II) - ортонормированный базис.Теорема 6. Пусть 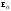 - евклидово пространство, - евклидово пространство,  - ортогональный оператор в - ортогональный оператор в 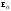 . Тогда . Тогда  в любом ортонормированном базисе задается ортогональной матрицей. в любом ортонормированном базисе задается ортогональной матрицей. Определение 9. Линейный оператор  в евклидовом пространстве в евклидовом пространстве 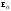 называется самосопряженным (симметрическим), если называется самосопряженным (симметрическим), если 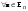 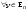 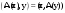 . .Определение 10. Матрица 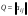 , , 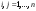 , называется симметрической, если , называется симметрической, если 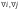 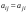 . .Теорема 7. Пусть 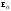 - евклидово пространство, - евклидово пространство, 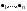 (I) - ортонормированный базис в (I) - ортонормированный базис в 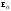 , ,  - симметрический оператор в - симметрический оператор в 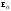 . Тогда матрица оператора . Тогда матрица оператора  в (I) симметрическая. в (I) симметрическая. Теорема 8. Если линейный оператор  , определенный в евклидовом пространстве , определенный в евклидовом пространстве 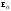 , задается хотя бы в одном ортонормированном базисе симметрической матрицей, оператор , задается хотя бы в одном ортонормированном базисе симметрической матрицей, оператор  - симметрический. - симметрический. Теорема 9. Пусть 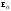 - евклидово пространство, - евклидово пространство,  - линейный оператор в - линейный оператор в 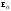 . Оператор . Оператор  является симметрическим тогда и только тогда, когда в является симметрическим тогда и только тогда, когда в 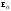 существует ортонормированный базис, составленный из собственных векторов оператора существует ортонормированный базис, составленный из собственных векторов оператора  Определение 8. Пусть  - линейное пространство, - линейное пространство,  - линейный оператор в - линейный оператор в  . Вектор . Вектор 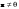 называется собственным вектором оператора называется собственным вектором оператора  , если найдется действительное число , если найдется действительное число  такое, что такое, что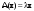 . .Число  называется собственным значением, соответствующим данному собственному вектору называется собственным значением, соответствующим данному собственному вектору  . .Квадратичные формы. Линейные преобразования неизвестных. Определение 1. Квадратичной формой от  неизвестных неизвестных 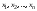 называется сумма вида называется сумма вида 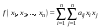 , (14.1) , (14.1)или развернуто 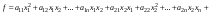 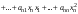 . (14.2) . (14.2)Определение 2. Линейным преобразованием неизвестных называется такой переход от системы  неизвестных неизвестных 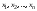 к системе к системе  неизвестных неизвестных 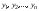 , при котором старые неизвестные выражаются через новые линейно с некоторыми коэффициентами: , при котором старые неизвестные выражаются через новые линейно с некоторыми коэффициентами: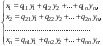 (14.4) (14.4)(14.5) Определение 3. Линейное преобразование неизвестных с матрицей 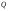 называется невырожденным, если называется невырожденным, если 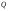 - невырожденная матрица. - невырожденная матрица. Теорема 1. Пусть вслед за линейным преобразованием (14.4) с матрицей 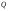 выполняется линейное преобразование выполняется линейное преобразование 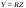 с матрицей с матрицей  , ,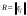 , ,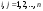 . Результирующее преобразование будет линейным с матрицей . Результирующее преобразование будет линейным с матрицей 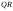 . .Утверждение 1. Для любых двух матриц А и В 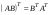 . .Теорема 2. Квадратичная форма от n неизвестных с матрицей  после выполнения линейного преобразования неизвестных с матрицей после выполнения линейного преобразования неизвестных с матрицей 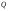 превращается в квадратичную форму от новых неизвестных с матрицей превращается в квадратичную форму от новых неизвестных с матрицей 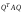 . .Утверждение 2. Ранг произведения матриц не выше ранга сомножителей. Утверждение 3. Ранг произведения произвольной матрицы  на невырожденную квадратную матрицу на невырожденную квадратную матрицу 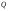 слева или справа равен рангу слева или справа равен рангу  . .Следствие из теоремы 2. Ранг квадратичной формы не изменяется при выполнении невырожденного линейного преобразования неизвестных. Определение 4. Каноническим видом квадратичной формы 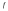 называют сумму квадратов неизвестных с некоторыми коэффициентами. называют сумму квадратов неизвестных с некоторыми коэффициентами. Замечание. Число отличных от нуля коэффициентов в каноническом виде квадратичной формы равно рангу формы. Теорема 3 (основная теорема о квадратичных формах). Всякая квадратичная форма может быть приведена некоторым невырожденным линейным преобразованием к каноническому виду. Положительно определенные квадратичные формы. Критерий Сильвестра.Определение 5. Нормальным видом квадратичной формы называется сумма квадратов неизвестных с коэффициентами «+!» или « 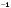 ». ».Теорема 4. Всякую квадратичную форму можно привести некоторым невырожденным линейным преобразованием неизвестных к нормальному виду. Определение 6. Квадратичная форма от n неизвестных называется положительно определенной, если она приводится к нормальному виду, содержащему n квадратов неизвестных с коэффициентами «+1»: 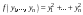 Теорема 5. Квадратичная форма 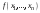 является положительно определенной тогда и только тогда, когда при любых значениях неизвестных, хотя бы одно из которых отлично от нуля, эта форма принимает положительные значения. является положительно определенной тогда и только тогда, когда при любых значениях неизвестных, хотя бы одно из которых отлично от нуля, эта форма принимает положительные значения.Теорема 6 (критерий Сильвестра). Квадратичная форма 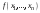 является положительно определенной тогда и только тогда, когда все ее главные миноры строго положительны. является положительно определенной тогда и только тогда, когда все ее главные миноры строго положительны. |
