определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Матрица линейного оператора. Связь координат образа и прообраза.Определение 3. Пусть  - линейное пространство, - линейное пространство, 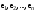 - базис в - базис в  , ,  - линейный оператор в - линейный оператор в  . Матрицей линейного оператора . Матрицей линейного оператора  в базисе в базисе 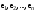 называется матрица называется матрица 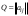 , , 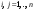 , такая, что , такая, что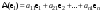 , ,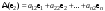 , ,…………………………………….. (12.1) 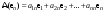 . .Замечание 1. Столбцы матрицы 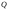 являются координатами в разложении векторов являются координатами в разложении векторов 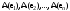 по базису по базису 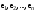 . .Замечание 2. Пусть  - линейное пространство, - линейное пространство,  - линейный оператор в - линейный оператор в  , , 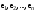 (I) - базис в (I) - базис в  . Матрица оператора в базисе (I) определена однозначно. . Матрица оператора в базисе (I) определена однозначно.Теорема 1. Пусть  - линейное пространство, - линейное пространство, 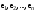 (I) - базис в (I) - базис в  , ,  - линейный оператор в - линейный оператор в  , , 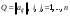 - матрица линейного оператора - матрица линейного оператора  в базисе (I), в базисе (I), 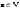 , , 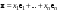 , , 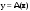 , , 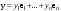 . Тогда . Тогда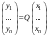 . .Теорема 3. Пусть  - линейное пространство, - линейное пространство, 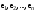 - базис в - базис в  , , 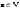 . Координаты . Координаты  относительно базиса определены однозначно. относительно базиса определены однозначно.Характеристический многочлен и характеристические корни матрицы.Определение 4. Квадратные матрицы  и и  называются подобными, если существует невырожденная матрица называются подобными, если существует невырожденная матрица 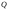 , такая, что , такая, что 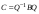 . .Теорема 2. Пусть  - линейное пространство, - линейное пространство, 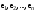 (I) и (I) и 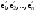 (II) - два базиса в (II) - два базиса в  , ,  - матрица перехода от (I) к (II), - матрица перехода от (I) к (II),  - линейный оператор в - линейный оператор в  , ,  - матрица оператора - матрица оператора  в (I), в (I),  - матрица оператора - матрица оператора  в (II). Тогда в (II). Тогда 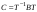 . .Определение 5. Многочлен 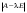 называется характеристическим многочленом матрицы называется характеристическим многочленом матрицы  , а его корни - характеристическими корнями матрицы , а его корни - характеристическими корнями матрицы  . .Теорема 3. Подобные матрицы имеют одинаковый набор характеристических корней. Следствие. Матрицы, задающие линейный оператор в различных базисах, имеют один набор характеристических корней (теорема 2 + теорема 3). |
