определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Характеристические корни и собственные значения линейного оператора.Определение 6. Характеристические корни матрицы линейного оператора (в любом базисе) называются характеристическими корнями линейного оператора. Определение 7. Весь набор характеристических корней называется спектром оператора. Определение 8. Пусть  - линейное пространство, - линейное пространство,  - линейный оператор в - линейный оператор в  . Вектор . Вектор 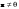 называется собственным вектором оператора называется собственным вектором оператора  , если найдется действительное число , если найдется действительное число  такое, что такое, что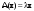 . .Число  называется собственным значением, соответствующим данному собственному вектору называется собственным значением, соответствующим данному собственному вектору  . .Теорема 4. Действительные характеристические корни линейного оператора, если они существуют, и только они, служат собственными значениями линейного оператора. Линейные операторы с простым спектром.Теорема 5. Пусть  - линейное пространство, - линейное пространство,  - линейный оператор в - линейный оператор в  , , 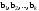 - собственные векторы оператора - собственные векторы оператора  , отвечающие собственным значениям , отвечающие собственным значениям 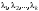 . Если . Если 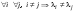 , то , то 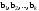 - линейно независимы. - линейно независимы.Определение 9. Линейный оператор  называется линейным оператором с простым спектром, если все его характеристические корни действительны и различны. называется линейным оператором с простым спектром, если все его характеристические корни действительны и различны.Теорема 6. Всякий линейный оператор с простым спектром может быть задан диагональной матрицей. Евклидовы пространства. Определения и примеры. Следствия из аксиом.Определение 1. Евклидовым пространством 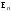 называется n-мерное линейное пространство, в котором каждой паре векторов называется n-мерное линейное пространство, в котором каждой паре векторов 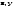 поставлено в соответствие вещественное число, называемое скалярным произведением векторов поставлено в соответствие вещественное число, называемое скалярным произведением векторов  и и  (это число обозначим (это число обозначим 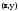 ), причем выполняются следующие аксиомы: ), причем выполняются следующие аксиомы:1. 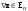 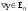 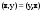 ; ;2. 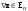 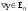 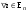 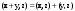 ; ;3. 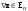 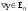 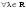 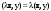 ; ;4. 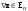 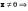 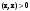 . .Замечание. Аксиомы 2 и 3 справедливы также в форме 2’: 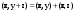 и форме 3’: и форме 3’: 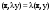 . . |
