определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Базис линейного пространства. Примеры базисов в конкретных пространствах.Определение 2. Пусть  - линейное пространство. Вектор - линейное пространство. Вектор  называется линейной комбинацией векторов называется линейной комбинацией векторов 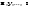 , если найдутся такие числа , если найдутся такие числа 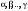 , что , что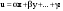 . .Определение 3. Система векторов 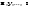 , принадлежащих линейному пространству , принадлежащих линейному пространству  , называется линейно зависимой, если найдутся такие числа , называется линейно зависимой, если найдутся такие числа 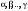 , не все равные нулю одновременно, что выполняется равенство , не все равные нулю одновременно, что выполняется равенство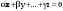 . .Определение 3'. Система векторов 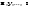 , принадлежащих линейному пространству , принадлежащих линейному пространству  , называется линейно зависимой, если один из векторов является линейной комбинацией остальных. , называется линейно зависимой, если один из векторов является линейной комбинацией остальных.Определение 4. Система векторов 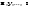 , принадлежащих линейному пространству , принадлежащих линейному пространству  , называется линейно независимой, если из равенства , называется линейно независимой, если из равенства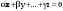 следует, что 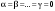 . .Теорема 1. Всякая система векторов, содержащая нулевой вектор, линейно зависима. Теорема 2. Всякая система векторов 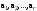 , содержащая линейно зависимую подсистему , содержащая линейно зависимую подсистему 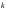 векторов, векторов, 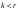 , линейно зависима. , линейно зависима.Определение 5. Система векторов 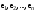 линейного пространства линейного пространства  называется базисом в называется базисом в  , если: , если: 1) 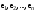 линейно независима; линейно независима;2) 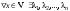 (вещественные числа): (вещественные числа):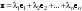 . (10.3) . (10.3)Правая часть равенства (10.3) называется разложением вектора  по базису по базису 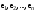 , а числа , а числа 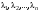 - координатами вектора - координатами вектора  в базисе в базисе 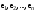 . .Приведем примеры базисов в конкретных линейных пространствах. Базис линейного пространства. Единственность разложения вектора по базису.Теорема 3. Пусть  - линейное пространство, - линейное пространство, 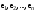 - базис в - базис в  , , 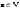 . Координаты . Координаты  относительно базиса определены однозначно. относительно базиса определены однозначно.Базис линейного пространства. Координаы суммы векторов и произведения вектора на число.Теорема 4. Пусть  - линейное пространство, - линейное пространство, 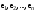 - базис в - базис в  . При сложении любых двух векторов их соответствующие координаты складываются, при умножении вектора на число каждая координата умножается на это число. . При сложении любых двух векторов их соответствующие координаты складываются, при умножении вектора на число каждая координата умножается на это число.Теорема 5. Пусть  - линейное пространство, - линейное пространство, 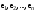 - базис в - базис в  . Всякая система . Всякая система  векторов векторов 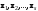 при при 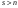 линейно зависима. линейно зависима. Следствие. Все базисы линейного пространства  состоят из одного и того же числа векторов. состоят из одного и того же числа векторов. |
