определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Метод Гаусса решения систем линейных уравнений.Определение 1. Решением системы линейных уравнений (8.1) называется такой набор чисел 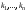 , что каждое из уравнений (8.1) обращается в тождество после замены неизвестных , что каждое из уравнений (8.1) обращается в тождество после замены неизвестных 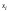 числами числами 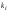 , , 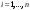 . .Определение 2. Система (8.1) называется несовместной, если она не имеет решений, и совместной, если она имеет решения. Определение 3. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений более одного. Определение 4. Две системы линейных уравнений называются эквивалентными, если они обе несовместны, или обе совместны и имеют одни и те же решения. Правило Крамера.)Теорема 1. Если 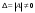 , то система (9.1) имеет, притом единственное, решение. , то система (9.1) имеет, притом единственное, решение.Правило Крамера: если 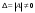 , то решение системы (9.1) может быть найдено по формулам , то решение системы (9.1) может быть найдено по формулам 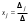 , , 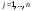 , где , где 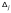 - определитель, который получится из - определитель, который получится из  , если столбец коэффициентов при , если столбец коэффициентов при 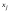 заменить столбцом свободных членов. заменить столбцом свободных членов.Теорема Кронекера-Капелли.Теорема 2 (Кронекера - Капелли). Система совместна тогда и только тогда, когда 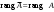 . .Определение 1. Формула, выражающая решение системы (9.4) в виде вектор-функции 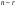 свободных неизвестных, называется общим решением системы (9.4): свободных неизвестных, называется общим решением системы (9.4):Система линейных однородных уравнений. Фундаментальная система решений.Теорема 3. Любая линейная комбинация решений системы однородных линейных уравнений (9.8) является решением системы (9.8). Определение 2. Пусть дана система линейных однородных уравнений с n неизвестными 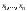 и матрицей и матрицей  , , 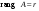 . Пусть неизвестные . Пусть неизвестные 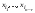 являются свободными. являются свободными.Теорема 4. Пусть дана система линейных однородных уравнений с матрицей  , , 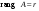 , и , и 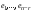 - фундаментальная система решений. Тогда всякое решение системы является линейной комбинацией решений - фундаментальная система решений. Тогда всякое решение системы является линейной комбинацией решений 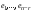 . .Аксиоматическое определение линейного пространства. Примеры. Следствия из аксиом.Определение 1. Совокупность  элементов элементов 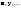 произвольной природы называется линейным пространством, если для любых элементов произвольной природы называется линейным пространством, если для любых элементов  и и  из из  установлено понятие суммы установлено понятие суммы 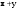 , а для любого элемента , а для любого элемента  из из  и любого действительного числа и любого действительного числа  установлено понятие произведения элемента установлено понятие произведения элемента  на число на число  , обозначаемое , обозначаемое 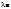 . При этом для введенных операций выполнены следующие восемь аксиом: . При этом для введенных операций выполнены следующие восемь аксиом:1. Сложение коммутативно: 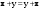 . . 2. Сложение ассоциативно: 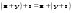 . . 3. Существует нулевой вектор  , удовлетворяющий условию , удовлетворяющий условию 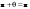 для всех для всех  . .4. Для любого вектора  существует противоположный вектор существует противоположный вектор  , удовлетворяющий условию , удовлетворяющий условию 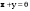 . .Для любых векторов  , ,  и любых действительных чисел и любых действительных чисел 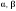 имеют место равенства: имеют место равенства:5. 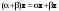 . .6. 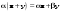 . .7. 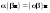 . .8. 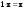 . .Укажем некоторые следствия из аксиом. Единственность нулевого элемента. 2. Единственность противоположного элемента. 3. Существование и единственность разности. Для любого вещественного числа  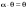 . .5. Для любого вектора 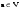 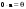 . .6. Если 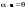 , то либо , то либо 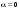 , либо , либо 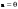 . . 7. 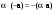 ; ;8. 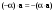 . . |
