определения линейная алгебра. Определения. Определение определителя порядка n, его свойства
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Определение определителя порядка n, его свойства.Определение 1. Матрицей называется прямоугольная таблица чисел. Определение 2. Определителем порядка  , соответствующим матрице (6.1), называется алгебраическая сумма , соответствующим матрице (6.1), называется алгебраическая сумма  членов, составленная следующим образом: членами определителя служат всевозможные произведения членов, составленная следующим образом: членами определителя служат всевозможные произведения  элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем слагаемое берется со знаком "+", если множество вторых индексов является четной перестановкой чисел элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем слагаемое берется со знаком "+", если множество вторых индексов является четной перестановкой чисел 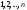 , и со знаком "–", если нечетной. , и со знаком "–", если нечетной.Замечание. Определение 2 для 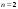 и и 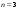 приводит к уже знакомым нам определителям 2-го и 3-го порядка: приводит к уже знакомым нам определителям 2-го и 3-го порядка:Свойства определителя порядка п: 1. 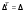 (определитель не меняется при транспонировании вокруг главной диагонали). (определитель не меняется при транспонировании вокруг главной диагонали).2. Если одна из строк определителя состоит из нулей, определитель равен нулю. 3. От перестановки двух строк определитель меняет лишь знак. 4. Определитель, содержащий две одинаковые строки, равен нулю. 5. Если все элементы некоторой строки определителя умножить на число 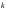 , определитель умножится на , определитель умножится на 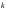 . .6. Определитель, содержащий две пропорциональные строки, равен нулю. 7. Если все элементы  -й строки определителя представлены в виде суммы -й строки определителя представлены в виде суммы 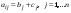 , то определитель равен сумме двух определителей, у которых все строки, кроме , то определитель равен сумме двух определителей, у которых все строки, кроме  -й, такие же, как в исходном определителе, а -й, такие же, как в исходном определителе, а  -я строка в одном определителе состоит из -я строка в одном определителе состоит из 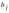 , а в другом - из , а в другом - из 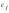 . .Определение 3.  -я строка определителя называется линейной комбинацией остальных его строк, если -я строка определителя называется линейной комбинацией остальных его строк, если 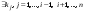 такие, что, умножая такие, что, умножая 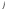 -ю строку на -ю строку на 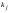 , а затем складывая все строки, кроме , а затем складывая все строки, кроме  -й, получаем -й, получаем  -ю строку. -ю строку.8. Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю. 9. Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число. Замечание. Мы сформулировали свойства определителя для строк. В силу свойства 1 ( 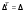 ) они справедливы и для столбцов. ) они справедливы и для столбцов.Определение 4. Алгебраическим дополнением 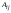 элемента элемента 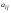 определителя определителя  называется его минор, умноженный на называется его минор, умноженный на 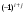 , где , где  - номер строки, - номер строки, 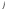 - номер столбца, в которых расположен выбранный элемент - номер столбца, в которых расположен выбранный элемент 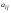 . .Теорема 1 (о разложении по строке). Определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения. Замечание. Можно вначале упростить определитель, воспользовавшись свойством 9, а затем использовать теорему 1. Тогда вычисление определителя порядка  сведется к вычислению всего одного определителя порядка сведется к вычислению всего одного определителя порядка 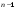 . . |
