поурочные планы математика 4 класс Школа России. поурочные планы математика. Основные требования к знаниям, умениям и навыкам учащихся к концу 4 класса учащиеся должны знать
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Для закрепления письменных приемов сложения и вычитания можно предложить учащимся решить с комментированием задание 312. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы познакомились с новым видом уравнений, учились их решать. Учитель. Каким правилом мы пользовались при решении уравнений? Дети. Если из суммы вычесть одно слагаемое, то получим другое. Домашнее задание: задание 315; тетрадь № 1, с. 41, № 1–3. У р о к 49 Нахождение неизвестного уменьшаемого Цели: познакомить с решением уравнений на основе связи уменьшаемого с вычитаемым и разностью; закрепить умения складывать и вычитать многозначные числа; повторить знания соотношений единиц длины и времени; вспомнить нахождение числа по его части и нахождение части от числа. Ход урока I. Организационный момент. II. Устный счёт. 1. Вычислите суммы удобным способом. 72 + 43 + 18 + 57 120 + 65 + 15 64 + 29 + 61 + 36 460 + 380 + 20 2.Задания на смекалку. 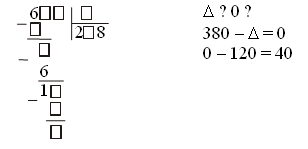 3. Задание 323 (вынести на доску). 9 см = … мм 9 ч = … мин 80 см = … мм 80 с = … мин … с 2 м 25 см = … мм 2 ч 25 мин = … мин III. Работа над новым материалом. Перед разбором новой темы учитель должен повторить с учащимися взаимосвязь между компонентами и результатом вычитания. С этой целью устно выполняется задание 317. Можно данную в учебнике таблицу записать заранее на доске, чтобы вызываемые к доске ученики заполнили пустые клетки в ней, каждый раз поясняя, как они находят неизвестное уменьшаемое или вычитаемое.
После заполнения всей таблицы учащиеся формулируют общие выводы: если к разности прибавить вычитаемое, то получится уменьшаемое. Если из уменьшаемого вычесть разность, то получится вычитаемое. 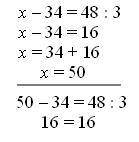 После этого учитель объясняет решение одного уравнения. Учитель. В уравнении х – 34 = 48 : 3 неизвестно уменьшаемое, вычитаемое 34, а разность выражена частным чисел 48 и 3. Найдем сначала разность (48 : 3 = 16). Значит, разность равна 16. Чтобы найти неизвестное уменьшаемое, надо разность и вычитаемое сложить. Вычисляем: 34 + 16 = 50. Значит, х = 50. Выполним проверку, подставив вместо х найденное число: 50 – 34 = 16 и 48 : 3 = 16. В левой и правой части уравнения получили одно и то же число. Значит, уравнение решено верно. Для закрепления полученных знаний учитель просит учащихся открыть учебник на с. 65 и объяснить решение второго уравнения и проверку к нему. Затем дети с подробным комментированием записывают и решают уравнения из задания 318. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. Под руководством учителя учащиеся разбирают задачу 321. Дети записывают краткое условие, составляют план решения, а после этого работают самостоятельно. Всего – 300 м. Занято 8 рядов по ? м. Осталось – 140 м. 1) 300 – 140 = 160 (м.) – занято 2) 160 : 8 = 20 (м.) О т в е т: 20 мест в каждом ряду. Перед выполнением задания 322 учитель должен вспомнить с учащимися, как найти часть от числа и как найти число по его части. Затем дети работают самостоятельно: чертят отрезки заданной длины. 2. Решение примеров. Для самостоятельной работы учащимся можно предложить решить примеры столбиком с проверкой – задание 319. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы учились решать уравнения на вычитание и делать проверку к ним. Учитель. Что повторяли на уроке? Дети. Мы повторяли сложение и вычитание многозначных чисел, решали задачи, чертили отрезки заданной длины, повторяли также соотношение единиц длины и времени. Домашнее задание: задания 320, 324; тетрадь № 1, с. 42, № 4–7. У р о к 50 Нахождение суммы нескольких слагаемых. Закрепление пройденного. Решение задач Цели: познакомить учащихся с разными способами нахождения суммы нескольких слагаемых; закрепить навыки устных и письменных вычислений, умения решать задачи и уравнения. Ход урока I. Организационный момент. II. Устный счёт. 1. Задание 327 (вынести на доску). Расставьте скобки так, чтобы равенства стали верными. 640 – 480 : 6 + 360 = 400 160 : 4 · 2 + 10 = 30 120 + 120 : 4 + 6 = 132 60 – 54 : 6 : 3 = 17 2. Задание «Магический квадрат».
III. Работа пройденного материала. 1. Решение задач. Задачу 325 учитель разбирает вместе с учащимися. После чтения задачи записывается условие, а затем проводится беседа. 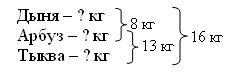 Учитель. Ребята, эту задачу можно решить несколькими способами. Что можно узнать, зная, что дыня и арбуз весят вместе 8 кг, а масса дыни, арбуза и тыквы вместе составляет 16 кг? Дети. Можно узнать массу тыквы. Учитель. Каким действием? Дети. Надо из 16 вычесть 8. Получится 8 кг. Учитель. Хорошо, массу тыквы узнали. Как узнать теперь массу арбуза, если арбуз и тыква весят 13 кг? Дети. Надо из 13 вычесть 8, получится 5 кг. Учитель. Хорошо. А теперь узнайте массу дыни. Дети. Надо из 8 вычесть 5, получится 3 кг. I способ: 1) 16 – 8 – 8 (кг) – тыква 2) 13 – 8 = 5 (кг) – арбуз 3) 8 – 5 = 3 (кг) – дыня Учитель. Ребята, кто догадался, как можно эту задачу решить другим способом? II способ: 1) 16 – 13 = 3 (кг) дыня 2) 8 – 3 = 5 (кг) – арбуз 3) 13 – 5 = 8 (кг) – тыква О т в е т: тыква – 8 кг, арбуз – 5 кг, дыня – 3 кг. Разбор задачи 326 провести под руководством учителя, а решение записать двумя способами. 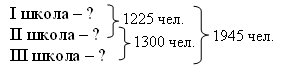 I способ: 1) 1 945 – 1 225 = 720 (чел.) – в III школе 2) 1 945 – 1 300 = 645 (чел.) – в I школе 3) 720 + 645 = 1 365 (чел.) – в I и III школах 4) 1 945 – 1 365 = 580 (чел.) – во II школе II способ: 1) 1 945 – 1 225 = 720 (чел.) – в III школе 2) 1 300 – 720 = 580 (чел.) – во II школе 3) 1 225 – 580 = 645 (чел.) – в I школе О т в е т: 645 человек – в I школе, 580 человек – во II школе, 720 человек – в III школе. 2. Решение уравнений. Решить задачи 328 с помощью составления уравнений дети могут самостоятельно. Учитель оказывает индивидуальную помощь тем детям, которые затрудняются. 3. Работа с величинами. Задание 330 учащиеся могут выполнить самостоятельно (с последующей проверкой). Ф и з к у л ь т м и н у т к а IV. Итоги урока. Учитель. Что повторяли на уроке? Дети. Мы решали задачи двумя способами, решали задачи, составляя уравнения, и работали с единицами длины, массы, времени. Домашнее задание: задания 329, 331; тетрадь № 1, с. 43, № 8, 9. У р о к 51 Сложение и вычитание величин Цели: познакомить учащихся с приемом письменного сложения и вычитания величин; совершенствовать вычислительные навыки и умения решать задачи и уравнения. Ход урока I. Организационный момент. II. Устный счет. 1. Решите и найдите лишнее уравнение. х – 26 = 14 х + 17 = 57 52 – х = 12 х – 17 = 13 90 – х = 50 2. Заполните таблицы. Перед заполнением таблиц учащиеся обязательно должны сказать правила, как найти слагаемое, уменьшаемое, вычитаемое.
III. Работа над новым материалом. Учитель. При решении многих практических задач приходится выполнять действия с величинами, значения которых выражены в разных единицах измерения. Если вычисления выполнить легко, то это делают устно. Например: 1 ч 20 мин + 35 мин, 12 ц 36 кг – 7 ц 20 кг Если же вычисления устно сделать трудно, то выполняют письменно по такому плану: 1) заменить крупные единицы мелкими; 2) выполнить заданное действие; 3) заменить мелкие единицы крупными. (Этот план можно записать на доске.) – Ребята, откройте учебник на с. 67 и посмотрите вверху оформление примеров такого вида. Дети открывают учебник и рассматривают запись. Для закрепления учащиеся выполняют с комментированием задания 332, 333, оформляя записи по образцу, данному в учебнике. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. Задачу 335 учащиеся решают под руководством учителя. Прочитав задачу, дети записывают краткое условие: Видеокассета – 210 мин 2 фильма – 1 ч 38 мин и 1 ч 27 мин Записать мультфильм – 23 мин – ? Потом ученики составляют план решения задачи и записывают решение на доске и в тетрадях в виде отдельных действий. 1 ч 38 мин = 98 мин 1 ч 27 мин = 87 мин 1) 98 + 87 = 185 (мин) – 2 фильма 2) 210 – 185 = 25 (мин) – остается 3) 25 мин > 23 мин О т в е т:на эту кассету можно записать мультфильм. 2. Решение примеров. Для самостоятельной работы на уроке учащимся можно предложить решить примеры из задания 336. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы учились складывать и вычитать величины. Учитель. Что повторяли на уроке? Дети. Повторили решение задач, уравнений. Домашнее задание: задание 334; тетрадь № 1, с. 44, № 10–12. У р о к 52 Задачи на увеличение и уменьшение числа на несколько единиц, сформулированные в косвенной форме Цели: познакомить учащихся с новым видом задач; закреплять умение складывать и вычитать величины; совершенствовать вычислительные навыки. Ход урока I. Организационный момент. II. Устный счёт. 1. Цепочка примеров.  2. Задание 342 (можно вынести на доску). Составьте по таблице задачу и запишите решение в виде выражений.
Перед заполнением таблицы учащиеся должны рассказать правило, как найти одну из величин, если известны две другие. Потом дети должны будут составить по этой таблице выражения, которые обозначают стоимость 6 карандашей и 2 кисточек; 5 карандашей и 1 линейки; 3 кисточек и линейки; карандаша, кисточки и линейки. 3. Арифметический диктант. Запишите число, которое следует за числом 50 000. Запишите число, в котором 89 ед. II кл. и 307 ед. I кл. Уменьшите число 400 на 230. Увеличьте число 500 на 360. Найдите сумму чисел 80 и 90. Найдите разность чисел 150 и 60. Выразите 25 000 м в километрах. Выразите 3 т в килограммах. III. Работа над новым материалом. Чтобы подвести учащихся к решению задач нового вида, учитель может провести с детьми практическую работу такого характера. Учитель. Нарисуйте у себя в тетради квадраты и кружки так, чтобы квадратов было 6 и чтобы их было на 2 больше, чем кружков. Сколько кружков нарисуете? Дети. 4 кружка. Учитель. Как узнали, что надо нарисовать 4 кружка? Дети. Из 6 вычесть 2. Учитель. Почему вычитали, ведь в задаче говорится «на 2 больше»? Дети. Это квадратов на 2 больше, а кружков на 2 меньше. Учитель. Верно. Теперь давайте откроем учебник на с. 68 и решим две задачи 338, а потом сравним их решение. Дети читают задачи и под руководством учителя записывают краткое условие и решение. З а д а ч а 338 (1). 1 дом – 9 эт. 2 дом – ?, на 3 эт. б. 9 + 3 = 12 (эт.) О т в е т: 12 этажей во втором доме. З а д а ч а 338 (2). 1 дом – 12 эт., это на 3 эт б. 2 дом – ? 12 – 3 = 9 (эт.) О т в е т: 9 этажей во втором доме. Учитель. Почему задачу 338 (2) решали вычитанием, там же сказано «на 3 этажа больше»? Дети. Это сказано про первый дом, значит, во втором доме наоборот, на 3 этажа меньше. После этого учащиеся решают с комментированием задачи 339 (1, 2). Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Сложение и вычитание величин. Задание 340 учащиеся выполняют с комментированием, записывая вычисления столбиком. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы познакомились с новым видом задач, учились их решать. Учитель. Что повторяли на уроке? Дети. Мы повторили сложение и вычитание величин, писали арифметический диктант. |
