2.12_Аналитический отчет PISA 2015. Отчет по результатам исследования pisa2015 Особенности проведения исследования pisa в России
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
|
ПРИМЕР 3. РАЦИОНАЛЬНОЕ РЫБОВОДСТВО
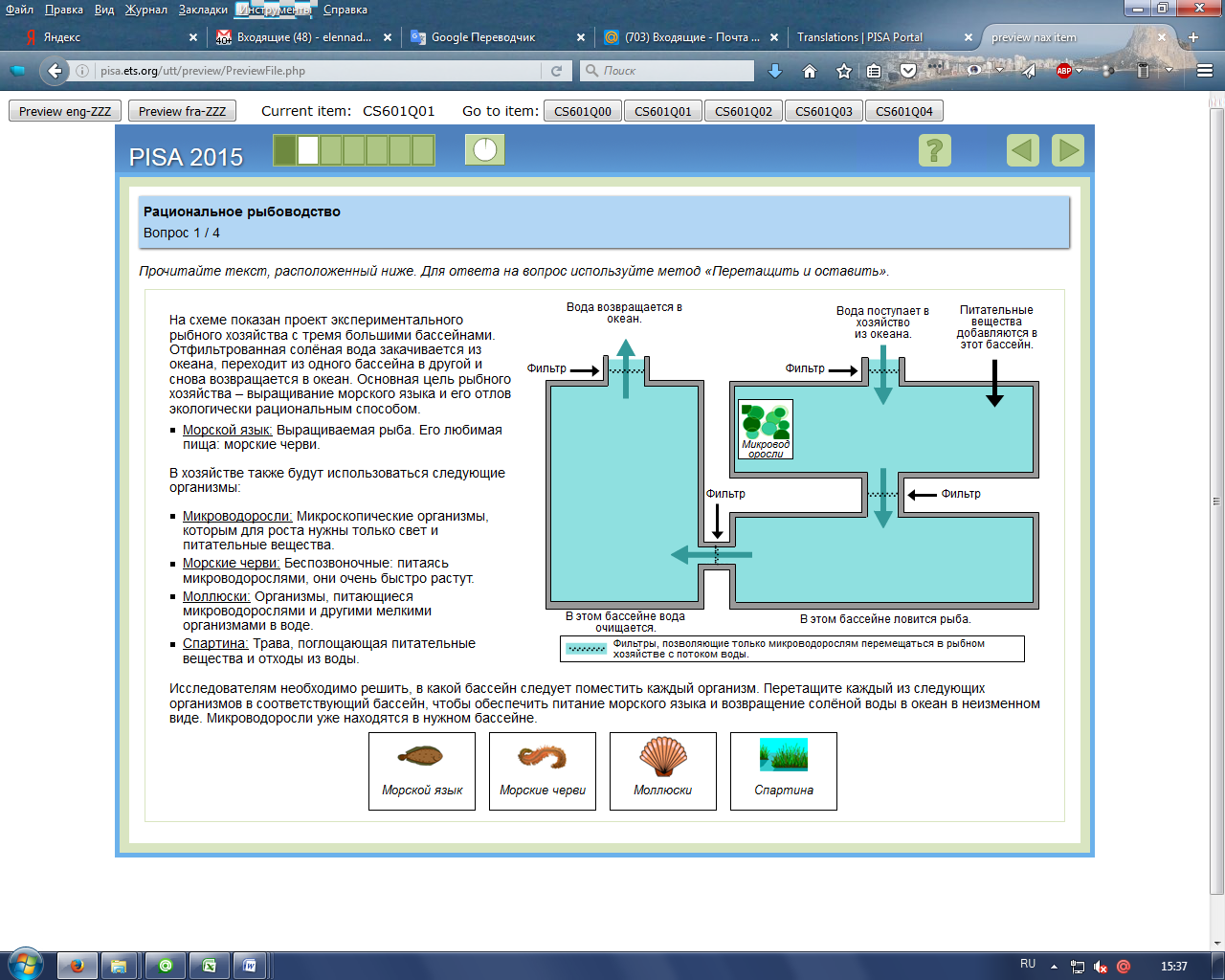
2.2. Сравнение результатов российских учащихся по естественнонаучной грамотности с результатами учащихся других стран Россия занимает 30-34 место в общем рейтинге результатов естественнонаучной грамотности всех стран (Таблица 6.6.). С учетом ошибки измерения результаты первых 27 стран рейтинга статистически значимо выше результата России, а результаты последующих 7 стран существенно не отличаются от него, поэтому Россия расположена на интервале 30-34 места среди 70 стран. В 2015 г. результаты Россия (487 баллов) ниже среднего балла OECD (493); 27 стран – выше России (баллы: 495 – 556); 7 стран – сравнимы с Россией (баллы: 332 – 473); 35 стран – ниже России (баллы: 332 – 493). Данные приведенные ниже в таблице 6.6. позволяют выявить тенденцию изменения успешности России по отношению к своим собственным результатам на протяжении 4 циклов исследования 2006 – 2015 гг. Таблица 6.6 Изменение положения российских учащихся по естественнонаучной грамотности среди стран-участниц исследования PISA
Как видно из приведенной таблицы с каждым циклом исследования Россия поднимается в общем рейтинге результатов естественнонаучной грамотности всех стран, средний балл России увеличивается и уменьшается количество стран значимо превышающих результат российских учащихся. 2.3. Тенденции изменения результатов естественнонаучной грамотности Анализ результатов российских учащихся за полный цикл исследования по естественнонаучной грамотности с 2006 года по 2015 год выявил повышение среднего балла российских учащихся по естественнонаучной грамотности с 479 до 487 (на 8 баллов) (Рис. 6.5.).  Рис. 6.5. Тенденция изменения среднего балла России по естественнонаучной грамотности. В распределении 15-летних учащихся по уровням естественнонаучной грамотности уменьшилось число учащихся, не достигших порогового значения естественнонаучной грамотности (2-го уровня по международной шкале) с 22% до 18% в сравнении с 2006 годом. При достижении данного уровня учащиеся начинают проявлять естественнонаучные компетенции, позволяющие им принимать участие в различных жизненных ситуациях, связанных с естествознанием и технологией. Число учащихся, достигших наивысшие уровни естественнонаучной грамотности (5-6 уровни), практически не изменилось (Рис. 6.6).  Рис. 6.6. Процентное распределение учащихся по уровням естественнонаучной грамотности. 3. Результаты исследования математической грамотности учащихся 15-летнего возраста 3.1. Основные результаты исследования математической грамотности учащихся 15-летнего возраста Одним из направлений исследования PISA является оценка готовности 15-летних учащихся к использованию математики для решения проблем, с которыми сталкиваются молодые люди в личных, учебных, профессиональных, общественных и научных аспектах повседневной жизни. В 2003 и 2012 гг. это направление было приоритетным и по сравнению с другими направлениями (ему уделялась значительно большая часть времени, отведенного на тестирование учащихся). В 2015 г. основным направлением было изучение естественнонаучной грамотности, поэтому время на изучение математической подготовки было ограничено. В связи с этим учащимся предлагалась только часть заданий исследования 2012 г. Содержание оценки математической подготовки 15-летних учащихся основано на понятии математической грамотности: «Математическая грамотность – это способность индивидуума формулировать, применять и интерпретировать математику в разнообразных контекстах. Она включает математические рассуждения, использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые необходимы конструктивному, активному и размышляющему гражданину»2. В основу организации области исследования математической грамотности положены три пересекающихся аспекта: математическое содержание, которое используется в тестовых заданиях, контекст, в котором представлена проблема, математические мыслительные процессы, которые описывают, что делает ученик, чтобы связать этот контекст с математикой, необходимой для решения поставленной проблемы. Для описания деятельности при решении задач были предложены три глагола: формулировать, применять и интерпретировать, которые явно отражают основные виды деятельности при решении проблем посредством использования математики. Они указывают на три мыслительных процесса, в которые, как правило, будут вовлечены учащиеся при активном участии в решении проблем: – формулировать ситуацию математически; – применять математические понятия, факты, процедуры размышления; – интерпретировать, использовать и оценивать математические результаты. Ниже приводится модель математической грамотности в исследовании PISA-2015.3 М 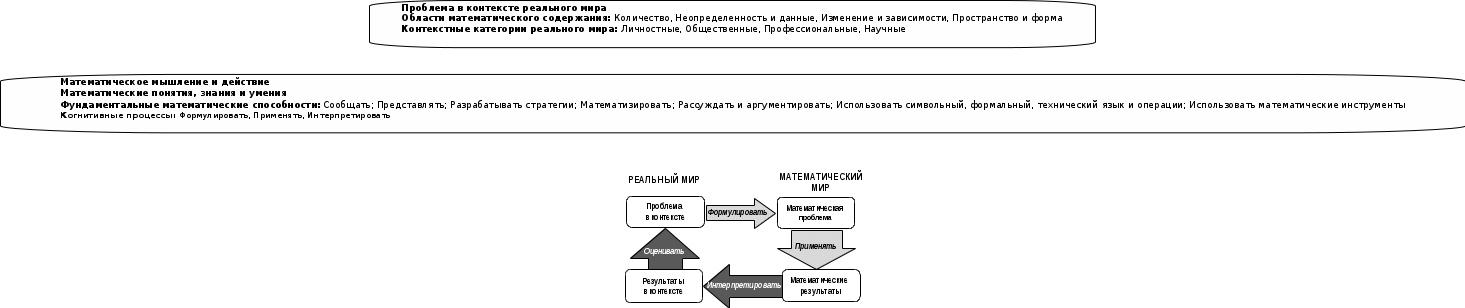 одель математической грамотности, реализованная в исследовании PISA-2015 На этой модели представлены основные конструкты в концепции оценки математической грамотности и связи между ними в исследовании PISA-2015, принятые всеми странами-участницами данного исследования. Содержимое самой большой рамки показывает, что математическая грамотность оценивается в контексте проблемы, которая возникает в реальном мире. Содержимое средней рамки освещает природу математического мышления и действия, которое может быть использовано для решения проблемы. Содержимое самой внутренней рамки описывает процессы, которые человек, решающий проблему, использует для конструирования решения.Подходы, которые используются в концепции оценки математической грамотности, отражают все главные компоненты её определения. Исследование отличают три акцента при оценке математической подготовки учащихся: соответствие подготовки нуждам учащихся в повседневной жизни; контекст, в рамках которого предложена проблема, должен быть действительно жизненным, а не выдуманным или притянутым за уши; «холистическое», а не фрагментарное применение математики, это означает, что требуется осуществить весь процесс от понимания проблемы, до ее формулирования, решения и сообщения результата, а не просто умение выполнить часть этого процесса (например, решить данное тригонометрическое уравнение, упростить данное алгебраическое выражение). При составлении заданий используются 4 категории контекстов: личная жизнь, образование/профессиональная деятельность, общественная жизнь и научная деятельность. Проблемы, которые ставятся в этих контекстах, являются частью опыта или практики участия учащихся в реальной окружающей действительности. Подобные проблемы можно противопоставить заданиям, характерным для школьных учебников математики, где главной целью является, скорее, попрактиковаться в математике, чем использовать ее для решения реальной проблемы. Эта подлинность в использовании математики – главный аспект планирования и анализа заданий в PISA, который тесно связан с определением математической грамотности. В исследовании математическое содержание распределено по четырем категориям: пространство и форма, изменение и зависимости, количество, неопределенность и данные, которые охватывают основные типы проблем, возникающих при взаимодействиях с повседневными явлениями. Название каждой из этих категорий отражает обобщающую идею (феноменологическую категорию), которая в общем виде характеризует специфику содержания заданий, относящихся к этой области. В совокупности эти обобщающие идеи охватывают круг математических тем, которые изучают учащие в школьном курсе математики. Именно из тематики содержания, охватываемого этими идеями, извлекаются соответствующие вопросы содержания, используемые для решения поставленной проблемы: Изменение и зависимости – задания, связанные с математическим описанием зависимости между переменными в различных процессах, т.е. с алгебраическим материалом; Пространство и форма – задания, относящиеся к пространственным и плоским геометрическим формам и отношениям, т.е. к геометрическому материалу; Количество – задания, связанные с числами и отношениями между ними, в программах по математике этот материал чаще всего относится к курсу арифметики; Неопределенность и данные – область охватывает вероятностные и статистические явления и зависимости, которые являются предметом изучения разделов статистики и вероятности. Согласно цели исследования задания, которые разрабатываются для включения в тесты, отличаются по содержанию и форме от привычных учебных заданий. Учащимся предлагается описание ситуации, приближенной к реальности, и 1-4 задания.Для выполнении этих заданий надо использовать информацию, представленную в описании ситуации, в некоторых заданиях требуется использовать жизненный опыт. Ответы учащихся на тестовые задания оцениваются в баллах и затем используются для расположения учащихся на шкале умелости (proficiency) в рамках конструкта математической грамотности, принятого в PISA. Положение учащегося на этой шкале и определяло уровень его математической грамотности. Структура и форма предъявления тестовых заданий в исследовании PISA-2015 При разработке тестовых заданий уделялось примерно одинаковое внимание к двум видам познавательной деятельности (формулировать и интерпретировать), которые обеспечивают связь между реальным и математическим миром, и большее внимание к познавательной деятельности, которая актуализируется при работе с математически сформулированной проблемой (Таблица 6.7.). Таблица 6.7. Распределение тестовых заданий по видам познавательной деятельности в 2015 г.
При распределении количества заданий по 4 областям содержания овладение материалом каждая из них считалось одинаково важным для математически грамотного гражданина. Поэтому в тесты было включено примерно одинаковое количество заданий по каждой области (Таблица 6.8.). Таблица 6.8. Распределение тестовых заданий по областям содержания в 2015 г.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
